
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории размерных цепейСодержание книги
Поиск на нашем сайте
1.1. Основные понятия и определения Размерной цепью называется совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи.
Например, совокупность размеров Размерные цепи принято изображать в виде отдельных схем (рис. 1.1, б). Размеры, образующие размерную цепь, называются звеньями размерной цепи. Звеньями размерных цепей могут быть линейные или угловые размеры. Ниже будем рассматривать только размерные цепи со звеньями в виде линейных размеров. Звенья этих размерных цепей принято обозначать прописными буквами русского алфавита (А, Б,...). В любой размерной цепи одно из звеньев является замыкающим, а остальные - составляющими звеньями. Замыкающим называют звено размерной цепи, являющееся исходным при постановке задачи или получающееся последним в результате ее решения. Например, очевидно, что именно исходя из требуемого значения зазора Замыкающее звено обозначается индексом Составляющие звенья размерной цепи делятся на увеличивающие и уменьшающие. Увеличивающим звеном называют такое, с увеличением которого замыкающее звено увеличивается. Уменьшающим звеном называют такое, с увеличением которого замыкающее звено уменьшается. В размерной цепи, показанной на рис. 1.1, звено Увеличивающие звенья обозначаются стрелкой над буквой, направленной вправо (
Задача выделения увеличивающих и уменьшающих звеньев для коротких размерных цепей оказывается достаточно простой. С увеличением числа звеньев в размерной цепи эта задача усложняется и для облегчения ее решения целесообразно использовать следующий прием. Замыкающему звену условно присваивают индекс уменьшающего, т.е. стрелка над его буквой направляется влево (рис. 1.2). Затем проводится мысленный обход размерного контура по этой стрелке и в направлении обхода расставляются стрелки над буквами, обозначающими составляющие звенья. Если стрелка будет направлена вправо - звено увеличивающее, а если влево - уменьшающее. Размерные цепи по назначению делятся на конструкторские, технологические и измерительные. Первые используют на этапе конструирования изделий, вторые - на этапе их изготовления, третьи - при измерении деталей. Звенья размерной цепи могут располагаться в одной или нескольких параллельных плоскостях и в непараллельных плоскостях. В первом случае размерную цепь называют плоской, во втором - пространственной. Причем в плоских размерных цепях звенья могут быть как параллельны, так и не параллельны друг другу. Ниже в основном будем рассматривать плоские размерные цепи с параллельными звеньями, которые широко используются при размерном анализе технологических процессов изготовления деталей. Основные уравнения Найдем зависимости между основными параметрами замыкающего звена и составляющих звеньев плоской размерной цепи с параллельными звеньями. Для этого сначала обратимся к рис. 1.1. Очевидно, что номинальное значение замыкающего звена
В общем случае при
Это уравнение принято называть уравнением размерной цепи. Очевидно (рис. 1.1), что наибольшее и наименьшее предельные значения замыкающего звена
В общем случае
Для установления зависимости между допуском замыкающего звена и допусками составляющих звеньев размерной цепи вычтем почленно из уравнения (1.2) уравнение (1.3). При этом получим
или окончательно
т.е. допуск замыкающего звена равен сумме допусков составляющих звеньев. Найдем зависимости между предельными отклонениями замыкающего звена и составляющих звеньев размерной цепи. Из схемы, приведенной на рис. 1.3, следует, что наибольшее и наименьшее предельные значения составляющих звеньев и замыкающего звена могут быть записаны в виде
В выражениях (1.5...1.8):
Вычитая почленно из этих уравнений уравнение (1.1), получим
Таким образом, верхнее отклонение замыкающего звена равно разности сумм верхних отклонений увеличивающих звеньев и нижних отклонений уменьшающих звеньев, а нижнее отклонение замыкающего звена равно разности сумм нижних отклонений увеличивающих звеньев и верхних отклонений уменьшающих звеньев. Установим зависимость между координатой середины поля допуска замыкающего звена (
Подставляя эти выражения в уравнения (1.9) и (1.10), имеем
Сложив почленно эти уравнения и разделив левую и правую части полученного в результате этого равенства на 2, получим следующую зависимость
т.е. координата середины поля допуска замыкающего звена равна разности сумм координат середин полей допусков увеличивающих и уменьшающих звеньев. Выразим среднее значение замыкающего звена (
Учитывая, что (см.рис.1.3)
будем иметь
т.е. среднее значение замыкающего звена равно разности сумм средних значений увеличивающих и уменьшающих звеньев. Зависимости (1.2... 1.4) и (1.9... 1.10) получены в предположении, что в размерной цепи возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих звеньев или их обратное сочетание. Метод расчета размерных цепей, основанный на использовании этих зависимостей, получил название метода максимума-минимума. Он обеспечивает полную взаимозаменяемость, исключая появление брака. Между тем, вероятность такого сочетания составляющих звеньев у конкретного изделия (детали) весьма мала. Это обстоятельство, а также законы распределения этих звеньев, учитываются в вероятностном методе расчета размерных цепей, который отличается от метода максимума-минимума расчетом допуска замыкающего звена. Полагая, что распределения размеров составляющих звеньев соответствуют нормальному закону, а границы полей рассеивания (6
или
Так как среднее значение замыкающего звена представляет собой алгебраическую сумму средних значений составляющих звеньев, то в соответствии с известной в теории вероятностей теоремой о дисперсии (
Учитывая соотношение (1.17), можно записать
или
Вероятностный метод расчета размерных цепей по сравнению с методом максимума-минимума позволяет, как будет показано ниже, увеличить допуски составляющих звеньев и, тем самым, снизить затраты на изготовление изделий (деталей). Причем с увеличением числа составляющих звеньев в размерной цепи это преимущество вероятностного метода возрастает. Вместе с тем, вероятностный метод расчета размерных цепей обеспечивает неполную взаимозаменяемость. Так, при расчете по формуле (1.18) у 0,27% изделий значение замыкающего звена может выйти за пределы поля допуска. Если распределение размеров составляющих звеньев отличается от нормального, то допуск замыкающего звена определяется по формуле [10]
где Для закона равной вероятности В заключении этого раздела отметим, что любая плоская размерная цепь с непараллельными звеньями может быть сведена к плоской размерной цепи с параллельными звеньями. Если плоская размерная цепь (см.рис.1.4) содержит составляющее звено (
Предельные отклонения звена
Таким образом, получим
|
||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 834; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.8 (0.008 с.) |

 Рис. 1.1. Конструкторская размерная цепь
Рис. 1.1. Конструкторская размерная цепь
 ,
, 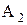 и
и  (рис. 1.1, а) образуют размерную цепь, которая определяет величину зазора
(рис. 1.1, а) образуют размерную цепь, которая определяет величину зазора  .
. ), а уменьшающие - стрелкой, направленной влево (
), а уменьшающие - стрелкой, направленной влево (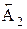 ).
). Рис. 1.2. Схема размерной цепи. Линией со стрелками показана последовательность «обхода» размерного контура для выделения увеличивающих и уменьшающих звеньев
Рис. 1.2. Схема размерной цепи. Линией со стрелками показана последовательность «обхода» размерного контура для выделения увеличивающих и уменьшающих звеньев
 .
.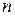 увеличивающих и
увеличивающих и  уменьшающих звеньев в размерной цепи получим
уменьшающих звеньев в размерной цепи получим . (1.1)
. (1.1) ;
; .
.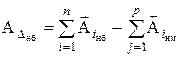 ; (1.2)
; (1.2) . (1.3)
. (1.3) ,
, , (1.4)
, (1.4) ; (1.5)
; (1.5) ; (1.6)
; (1.6) ; (1.7)
; (1.7) Рис.1.3. Схема размеров, допуска и отклонений
Рис.1.3. Схема размеров, допуска и отклонений
 . (1.8)
. (1.8)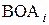 ,
,  - соответственно верхние отклонения составляющих звеньев и замыкающего звена;
- соответственно верхние отклонения составляющих звеньев и замыкающего звена;  ,
, 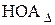 - соответственно их нижние отклонения. Подставляя эти выражения в уравнения (1.2) и (1.3), будем иметь
- соответственно их нижние отклонения. Подставляя эти выражения в уравнения (1.2) и (1.3), будем иметь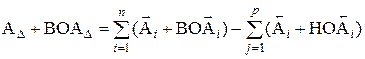 ;
; .
. ; (1.9)
; (1.9) . (1.10)
. (1.10) ) и координатами середин полей допусков составляющих звеньев (
) и координатами середин полей допусков составляющих звеньев (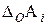 ). Для этого в соответствии со схемой (рис. 1.3) выразим предельные отклонения замыкающего звена и составляющих звеньев через координату середины поля допуска и допуск
). Для этого в соответствии со схемой (рис. 1.3) выразим предельные отклонения замыкающего звена и составляющих звеньев через координату середины поля допуска и допуск ; (1.11)
; (1.11) ; (1.12)
; (1.12) ; (1.13)
; (1.13) . (1.14)
. (1.14) ;
; .
. , (1.15)
, (1.15) ) через средние значения составляющих звеньев (
) через средние значения составляющих звеньев ( ). Для этого сложим почленно уравнение (1.15) и уравнение (1.1) В результате получим
). Для этого сложим почленно уравнение (1.15) и уравнение (1.1) В результате получим .
. ;
;
 , (1.16)
, (1.16) ) совпадают с границами их полей допусков, можно принять [10]
) совпадают с границами их полей допусков, можно принять [10]
 . (1.17)
. (1.17) ) суммы независимых случайных величин (составляющих звеньев) будем иметь
) суммы независимых случайных величин (составляющих звеньев) будем иметь .
.
 . (1.18)
. (1.18) ,
, - коэффициент относительного рассеивания.
- коэффициент относительного рассеивания. ), расположенное под углом
), расположенное под углом  к направлению замыкающего звена, то такое звено включается в размерную цепь своей проекцией (
к направлению замыкающего звена, то такое звено включается в размерную цепь своей проекцией ( ) на это направление. Предположим, что звено
) на это направление. Предположим, что звено  , угол
, угол  Рис. 1.4. Плоская размерная цепь
с непараллельными звеньями
Рис. 1.4. Плоская размерная цепь
с непараллельными звеньями
 (мм).
(мм). (мм);
(мм); (мм).
(мм). мм.
мм.


