
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи расчета технологических размеровСодержание книги
Поиск на нашем сайте
Рассмотрим решение задач, возникающих при расчете технологических размеров. Задача расчета технологических размеров из условия обеспечения минимального припуска на обработку. На рис.3.9 показана простейшая технологическая размерная цепь. Составляющими звеньями в этой цепи являются размер заготовки до обработки
Таким образом, в рассматриваемой технологической размерной цепи известно номинальное значение и предельные отклонения одного составляющего звена ( Решение этой задачи обычно выполняется методом максимума-минимума с использованием способа средних значений, т.е. на основе уравнения (1.16). Суть решения состоит в следующем. 1. Определяется среднее значение составляющего звена
Это звено представляется в виде 2. Находится среднее значение припуска
Учитывая, что
получим
3. Подсчитывается среднее значение звена
откуда
Звено Рассмотрим решение еще одной разновидности рассмотренной задачи. На рис.3.10 изображена технологическая размерная цепь, замыкающим звеном которой является припуск
Задача решается следующим образом. Находится допуск размера
Определяется среднее значение припуска
где Из уравнения
находится среднее значение размера
Номинальное значение размера
Задача расчета технологических размеров из условия обеспечения конструкторских размеров, непосредственно не выдерживаемых при изготовлении детали. На рис.3.11 дана технологическая размерная цепь, замыкающим звеном которой является конструкторский размер Проверяется возможность обеспечения спроектированным технологическим процессом требуемой точности конструкторского размера. Это делается в самом начале расчета технологических размеров. При расчете методом максимума-минимума условие обеспечения точности конструкторского размера записывается в виде
При расчете вероятностным методом (в предположении о нормальном распределении технологических размеров и
Если неравенства (3.7) или (3.8) выполняются, то затем из уравнения (см.рис.3.11)
находится среднее значение технологического размера
Этот размер записывается в виде Если указанные неравенства не выполняются, то необходимо либо несколько ужесточить допуски на технологические размеры (это потребует более частых подналадок технологических систем), либо внести упомянутые в начале этого раздела изменения в технологический процесс изготовления детали. При необходимости пересчета номинальных значений технологических размеров (с их средних значений) следует воспользоваться соотношением (3.6).
|
|||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.244 (0.005 с.) |

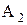 и ее размер после обработки
и ее размер после обработки  (выполняемый размер), замыкающим звеном – припуск на обработку
(выполняемый размер), замыкающим звеном – припуск на обработку  . Причем выполняемый размер
. Причем выполняемый размер  или найден из ранее рассмотренной технологической размерной цепи.
или найден из ранее рассмотренной технологической размерной цепи.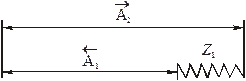 Рис.3.9. Простейшая технологическая размерная цепь с замыкающим звеном – припуском
Рис.3.9. Простейшая технологическая размерная цепь с замыкающим звеном – припуском
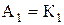 )
)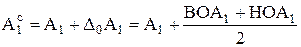 .
. .
.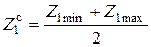 .
. ,
,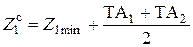 .
. ,
,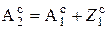 .
.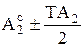 .
. , а составляющими звеньями – технологические размеры
, а составляющими звеньями – технологические размеры 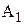 …
… 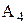 . Размеры
. Размеры 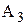 и
и 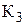 и
и  , размер
, размер 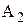 . Нужно определить его номинальное значение, используя метод максимума-минимума.
. Нужно определить его номинальное значение, используя метод максимума-минимума.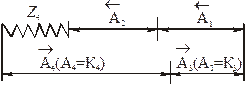 Рис.3.10. Технологическая размерная цепь с замыкающим звеном – припуском
Рис.3.10. Технологическая размерная цепь с замыкающим звеном – припуском
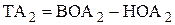 .
.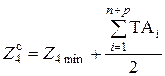 ,
, - сумма допусков составляющих звеньев (технологических размеров) размерной цепи.
- сумма допусков составляющих звеньев (технологических размеров) размерной цепи.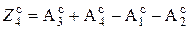
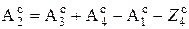 .
. . (3.6)
. (3.6)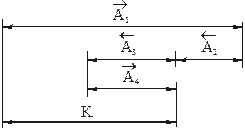 Рис.3.11. Технологическая размерная цепь с замыкающим звеном – конструкторским размером
Рис.3.11. Технологическая размерная цепь с замыкающим звеном – конструкторским размером
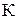 . В этой цепи известны номинальные значения и предельные отклонения составляющих звеньев (технологических размеров)
. В этой цепи известны номинальные значения и предельные отклонения составляющих звеньев (технологических размеров) 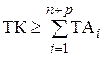 . (3.7)
. (3.7)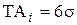 ) это условие принимает вид
) это условие принимает вид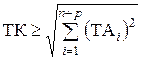 . (3.8)
. (3.8)
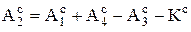 .
.


