
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение обратной задачи методом максимума-минимумаСодержание книги
Поиск на нашем сайте
Обратная задача, как уже отмечалось, является проверочной, позволяя, в частности, оценить правильность решения прямой задачи. Рассмотрим решение обратной задачи для рассматриваемой размерной цепи (рис.1.5). Значения параметров составляющих звеньев этой цепи примем такими, которые были получены выше в результате решения прямой задачи, т.е. Первый вариант решения 1. С помощью уравнения (1.1) находится номинальное значение замыкающего звена. Для рассматриваемого примера
2. По формуле (1.4) определяется допуск замыкающего звена. Для рассматриваемого примера
3. С помощью зависимости (1.15) вычисляется координата середины поля допуска замыкающего звена. Для рассматриваемого примера
4. По соотношениям (1.11) и (1.12) находятся предельные отклонения замыкающего звена. Для рассматриваемого примера
Таким образом, окончательно получим Второй вариант решения 1. Так же как в первом варианте находится номинальное значение замыкающего звена, т.е. будем иметь 2. С помощью уравнений (1.9) и (1.10) находятся предельные отклонения замыкающего звена. Для рассматриваемого примера
В итоге также получим Необходимо отметить, что для решения обратной задачи методом максимума-минимума могут быть использованы и другие варианты, например, вариант, основанный на использовании зависимостей (1.2) и (1.3). Решение прямой задачи вероятностным методом Так же как при решении этой задачи методом максимума-минимума для рассматриваемой размерной цепи (рис.1.5) примем Задача решается следующим образом. 1. Производится распределение допуска замыкающего звена между составляющими звеньями. Для решения этой локальной задачи имеется только одно уравнение (1.18), связывающее допуск замыкающего звена с допусками составляющих звеньев. Для рассматриваемого примера это уравнение может быть записано в виде
Примем
Таким образом, вероятностный метод по сравнению с методом максимума-минимума (см.раздел.1.3.1) дает возможность значительно увеличить допуски составляющих звеньев. Далее решение задачи полностью совпадает с ее решением методом максимума-минимума. 2. На все составляющие звенья, кроме одного, назначаются предельные отклонения. Примем 3.Для определения предельных отклонений звена Для рассматриваемого примера
Отсюда
Предельные отклонения звена
Таким образом, получим Решение обратной задачи вероятностным методом Рассмотрим решение этой задачи для параметров составляющих звеньев, найденных выше при решении прямой задачи, т.е. проверим правильность ее решения. Итак, имеем Задача решается следующим образом. 1.С помощью уравнения (1.1) находится номинальное значение замыкающего звена. Для рассматриваемого примера
2. По зависимости (1.18) определяется допуск замыкающего звена. Для рассматриваемого примера
3. С помощью уравнения (1.15) вычисляется координата середины поля допуска замыкающего звена. Для рассматриваемого примера
4. По зависимостям (1.11) и (1.12) находятся предельные отклонения замыкающего звена. Для рассматриваемого примера
Таким образом, получим
РАЗМЕРНЫЙ АНАЛИЗ СПРОЕКТИРОВАННЫХ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ
|
|||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.213.201 (0.009 с.) |

 =60+0,65 мм,
=60+0,65 мм, 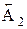 =10-0,05 мм,
=10-0,05 мм, 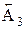 =40-0,05 мм и
=40-0,05 мм и  =9-0,05 мм.
=9-0,05 мм. (мм).
(мм).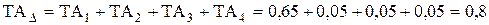 (мм).
(мм).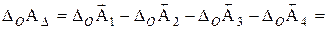
 (мм).
(мм).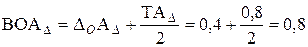 (мм);
(мм);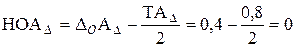 (мм).
(мм). =1+0,8 мм, т.е прямая задача решена верно.
=1+0,8 мм, т.е прямая задача решена верно.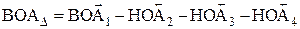 =0,65-(-0,05)-(-0,05)-(-0,05)=0,8 (мм);
=0,65-(-0,05)-(-0,05)-(-0,05)=0,8 (мм); =0-0-0-0=0 (мм).
=0-0-0-0=0 (мм).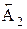 =10мм,
=10мм, 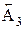 =40 мм и
=40 мм и 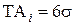 . Требуется найти допуски и предельные отклонения составляющих звеньев.
. Требуется найти допуски и предельные отклонения составляющих звеньев.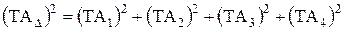 .
. =0,2 мм. Оставшуюся часть допуска замыкающего звена перенесем на составляющее звено
=0,2 мм. Оставшуюся часть допуска замыкающего звена перенесем на составляющее звено  . Допуск этого звена составит
. Допуск этого звена составит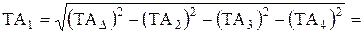
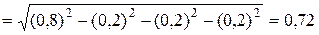 (мм).
(мм).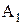 =600,72 мм,
=600,72 мм, 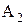 =10-0,2 мм,
=10-0,2 мм,  =40-0,2 мм.
=40-0,2 мм.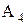 сначала вычисляется координата середины поля допуска этого звена. Затем находятся уже сами предельные отклонения.
сначала вычисляется координата середины поля допуска этого звена. Затем находятся уже сами предельные отклонения. ;
; .
.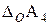 =0,16 (мм).
=0,16 (мм).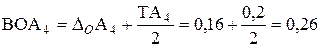 (мм);
(мм); (мм).
(мм).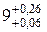 мм. Задача решена.
мм. Задача решена. =60+0,72 мм,
=60+0,72 мм,  =
= 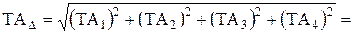
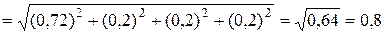 (мм).
(мм).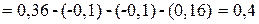 (мм).
(мм).


