
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резистивный элемент (резистор)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Резистивный элемент (резистор)
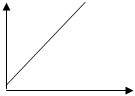
Величина обратная сопротивлению называется проводимостью. В простейшем случае сопротивление проводника длиной l и сечением S определяется выражением R = Величина обратная удельному сопротивлению Основной характеристикой резистивного элемента является зависимость напряжения от тока, называемая вольт-амперной характеристикой (ВАХ). Зависимость представляет собой прямую линию, проходящую через начало координат, если резистор представляет собой линейный элемент, описываемый законом Ома для участка цепи. U U = IR - закон Ома для участка цепи
I Сопротивление пассивного участка цепи в общем случае определяется по формуле: R=P/I2, где P - потребляемая мощность; I - ток.
Индуктивный элемент (катушка индуктивности)
Катушка индуктивности – это пассивный элемент, в котором энергия электрического поля запасается в виде магнитной энергии и характеризуется индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле. В общем случае индуктивность определяется по следующей формуле: L = Ψ/I, где L - индуктивность, Ψ-потокосцепление, I -протекающий ток. Потокосцепление определяется как сумма произведений потока, пронизывающего витки на число этих витков: Ψ= Основной характеристикой катушки индуктивности является зависимость потокосцепления от тока, называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость представляет собой прямую линию, проходящую через начало координат.
Пассивный - т.е. проходит через начало координат. I На схеме индуктивность обозначается:
Емкостный элемент (конденсатор)
Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета емкости необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению U между ними (Фарад). С = q/U [Ф] Фарад Основная характеристика конденсатора – кулон-вольтовская характеристика. Для линейного конденсатора представляет собой прямую линию, проходящую через начало координат. q C - const
U На схеме конденсатор обозначается следующим образом:
Метод контурных токов
Если цепь содержит много узлов и контуров, то расчет ЭЦ на основе применения з-в Кирхгофа связан с решением большого кол-ва уравнений. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. Введя понятие о контурных токах можно уменьшить кол-во уравнений на величину, равную составляемым по 1-му з-ну К-фа (у-1; где у – кол-во узлов). Порядок расчета: Выбираются независимые контуры, и задаются произвольные направления контурных токов. Контурные токи – условные (расчетные) токи, замыкающиеся в соответствующих контурах. Задача: найти все токи. После выбора положит. направления токов на схеме выбираются независим. контуры и положит. направления обхода каждого контура. Считается, что в каждом контуре циркулирует свой собственный контурный ток, направление которого совпадает с выбранным направлением в контуре. I1 = II; I2 = III - II; I3 = III; I4 = III –IIII; I5 = - IIII Для определения контурн. токов по 2-му закону К-фа составляются уравнения для выбранных контуров: 1) II (R1+R2) – III *R2 = E1 – E2 2) III (R2+R3 +R4) – II *R2 - IIII *R4 = E2 3) IIII (R4+R5) - III *R4 = - E3 Все резисторы, входящие в 1-й контур – R11, во 2-й - R22, в 3-й – R33.
R22 = R2 + R3 + R4 R33 = R4 + R5 Резисторы, общие с 1-м и 2-м контуром - R12 или R21, со 2-м и 3-м – R23 или R32, 1-м и 3-м - R13 или R31.
R13 = R31 = 0 R23 = R32 = R4 Источники тока или напряжения, входящие в 1-й контур – Е11 = Е1 - Е2; 2-й: Е22 = Е2; 3-й: Е33 = - Е3 Система уравнений будет представлена в след. виде:
- R21 * II + R22 * III – R23 * IIII = E22 - R31 * II – R32 * III + R33 * IIII = E33 На главной диагонали все положительные, остальные – отрицательные. Матричная форма записи системы удобна для решения системы при помощи ЭВМ. При расчете электрических цепей изложенным методом всегда стремятся к тому, чтобы число контурных токов, замыкающихся через каждую из ветвей, было по возможности минимальным. С этой целью обычно выбирают каждый контур в виде ячейки руководствуясь указанным выше правилом выбора независимых контуров при составлении уравнений на основании второго закона Кирхгофа, что возможно для любой планарной схемы. Положительные направления контурных токов можно выбирать и произвольно, т. е. независимо от положительных направлений токов в ветвях. Метод двух узлов Если имеется несколько ветвей, соединенных параллельно, в каждой из которых находятся источники напряжения и резистивное сопротивление, то все эти ветви можно заменить одной с некоторой эквивалентной
G =
При расчёте
Расщепление источников Для цепи с идеальными источниками тока справедливо следующее правило: Последовательно с идеальным источником тока можно включить любое количество таких же источников. Никакие изменений режимов в цепи не произойдет, Т.к. источник тока идеален и его внутреннее сопротивление равняется бесконечности. Если в последствии включить еще несколько таких же, то сопротивление участка цепи не изменится, а останется бесконечно большим, ток в цепи так же не изменится, т.к источник тока одинаковый, т.е. все параметры тока останутся прежними.
I1 = I2…. =I3 =In, Rвн=∞ Последовательное подключение нескольких одинаковых источников тока называется расщеплением источника тока. Расщеплять можно как источники тока, так и напряжения. Для расщепления идеального источника напряжения, параллельное ему подключаются один или несколько одинаковых источников напряжения при этом никаких изменений режимов в цепи происходить не будет.
R2 I R4
R2
R4
Если бы на отрезке ВЕ был бы подключен резистор R5, то мы бы заменили звезду на треугольник и получи ли бы:
15. Преобразование треугольника сопротивлений с источником напряжения в эквивалентную звезду Пусть имеется цепь (рис. 2, а).
Рис. 2. Преобразование треугольника сопротивлений с источником напряжения в эквивалентную звезду Требуется преобразовать данный треугольник в звезду. Если бы в схеме не было источника Е, то преобразование можно было произвести с помощью формул преобразования пассивного треугольника в пассивную звезду. Однако данные формулы справедливы только для пассивных цепей, поэтому в цепях с источниками необходимо проделать ряд преобразований. Заменим источник напряжения Е эквивалентным источником тока, цепь рис. 2, а приобретает вид рис. 2, б. В результате преобразования получился пассивный треугольник R1, R2, R3, который можно превратить в эквивалентную пассивную звезду, причем между точками АВ остается неизменнным источник J = E/Rt.
Расщепим источник J и соединим точку F с точкой 0 (на рис. 2, в показано штриховой линией). Теперь источники тока можно заменить эквивалентными источниками напряжения, при этом получается схема эквивалентной звезды с источниками напряжения (рис. 2, г).
Трехфазные цепи
Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой. Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными. Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС. Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю. На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита (А, В, С), а концы - последними буквами (X, Y, Z). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу. Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.
Мощность трехфазной цепи
Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками. Активная мощность трехфазной цепи равна сумме активных мощностей фаз:
Формула используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке. При симметричной нагрузке:
При соединении в треугольник симметричной нагрузки:
При соединении в звезду:
В обоих случаях:
Магнитные цепи Интенсивность магнитного поля характеризуется векторной величиной: напряженностью магнитного поля В зависимости от величины относительной магнитной проницаемости, все вещества делятся на три группы. 1) диамагнетики: вещества, у которых μ< 1. 2) парамагнетики, вещества с μ >1. 3) ферромагнетики, вещества с μ >> 1 (железо, никель, кобальт и многие сплавы из неферромагнитных веществ). Магнитная цепь-совокупность устройств, содержащих феромагнитные вещества. Процессы в магнитных цепях описываются с помощью понятий магнитодвижущей силы, магнитного потока. Магнитным потоком называется поток вектора магнитной индукции через поверхность S: Магнитодвижущая сила электромагнита 2. Свойства ферромагнитных материалов Поместим ферромагнитный материал внутри катушки с током. Сначала, с увеличением напряженности намагничивающего поля, Значение магнитной индукции при напряженности намагничивающего поля, равном нулю, называется остаточной магнитной индукцией Br, или остаточной намагниченностью. Напряженность магнитного поля НС при В = 0 называется коэрцитивной силой. Ферромагнитные материалы с большим значен коэрцитивной силы >4000А/м наз-ся магнитотвердыми.(изготавл постоян магниты.) 3. Расчет магнитных цепей. Основным законом, используемым при расчетах магнитных цепей, является закон полного тока. Он формулируется следующим образом: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Если контур интегрирования охватывает катушку с числом витков W, через которую протекает ток I, то алгебраическая сумма токов Обычно контур интегрирования выбирают таким образом, чтобы он совпадал с силовой линией магнитного поля, тогда векторное произведение в формуле (9.1) можно заменить произведением скалярных величин H╥dl. В практических расчетах интеграл Резистивный элемент (резистор)
Величина обратная сопротивлению называется проводимостью. В простейшем случае сопротивление проводника длиной l и сечением S определяется выражением R = Величина обратная удельному сопротивлению Основной характеристикой резистивного элемента является зависимость напряжения от тока, называемая вольт-амперной характеристикой (ВАХ). Зависимость представляет собой прямую линию, проходящую через начало координат, если резистор представляет собой линейный элемент, описываемый законом Ома для участка цепи. U U = IR - закон Ома для участка цепи
I Сопротивление пассивного участка цепи в общем случае определяется по формуле: R=P/I2, где P - потребляемая мощность; I - ток.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.009 с.) |

 Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Сопротивление измеряется в Омах. Сопротивление изображается на схеме: R
Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Сопротивление измеряется в Омах. Сопротивление изображается на схеме: R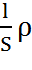 , где
, где 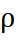 - удельное сопротивление материала [Ом/м].
- удельное сопротивление материала [Ом/м].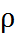 называется удельной проводимостью: j = 1/
называется удельной проводимостью: j = 1/ 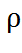 .
.
 , где w - число витков, Ф - поток магнитной индукции, пронизывающий каждый виток (Ф = ВS), В - вектор магнитной индукции, S - площадь рамки.
, где w - число витков, Ф - поток магнитной индукции, пронизывающий каждый виток (Ф = ВS), В - вектор магнитной индукции, S - площадь рамки.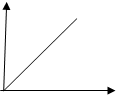 ψ Ψ = L * I, где L = const
ψ Ψ = L * I, где L = const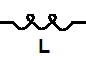
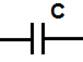
 R11 = R1 + R2
R11 = R1 + R2 R12 = R21 = R2
R12 = R21 = R2 R11 * II - R12 * III - R13 * IIII = E11
R11 * II - R12 * III - R13 * IIII = E11 и эквивалентное сопротивление
и эквивалентное сопротивление  .
.

 ;
; – проводимость электрической ветки;
– проводимость электрической ветки; ;
;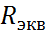 данной схемы необходимо помнить, что при расчёте числителя для
данной схемы необходимо помнить, что при расчёте числителя для  ;
;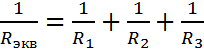 ;
; .
.




 Рассмотрим электрическую цепь в случаи, если необходимо преобразовать источник тока в источник напряжения. Причем к источнику тока параллельно подключена цепочка, состоящая из нескольких сопротивлений по каждому из которых протекают различные токи.
Рассмотрим электрическую цепь в случаи, если необходимо преобразовать источник тока в источник напряжения. Причем к источнику тока параллельно подключена цепочка, состоящая из нескольких сопротивлений по каждому из которых протекают различные токи.
 R1 R3 I
R1 R3 I I B E E A B E
I B E E A B E
 R1 R3
R1 R3



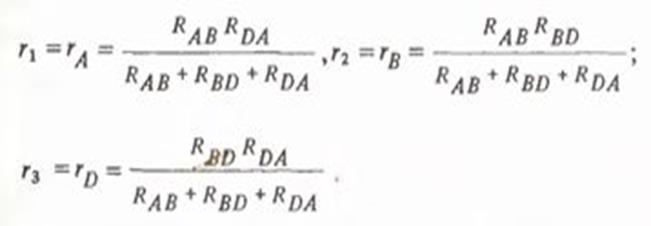
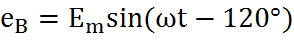
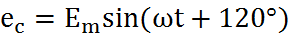
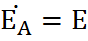
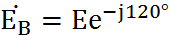
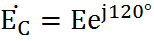
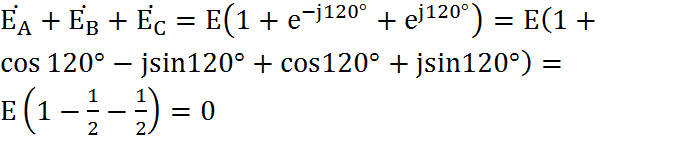 Соответственно
Соответственно 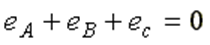
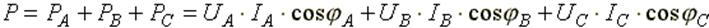
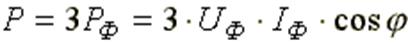
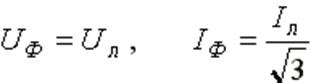
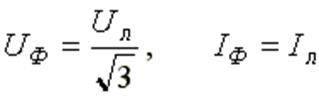
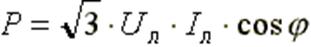
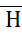 , измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором магнитной индукции
, измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором магнитной индукции 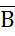 , измеряемой в теслах (Тл). Напряженность магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей среды.
, измеряемой в теслах (Тл). Напряженность магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей среды. 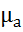
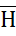 = μ0 μ
= μ0 μ 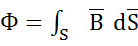 . Магнитный поток измеряется в веберах (Вб). Источником магнитодвижущей силы является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током).
. Магнитный поток измеряется в веберах (Вб). Источником магнитодвижущей силы является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током).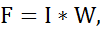 где I - ток, протекающий в катушке; W - число витков катушки. В магнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности.
где I - ток, протекающий в катушке; W - число витков катушки. В магнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности. магнитная индукция быстро возрастает. Затем, из-за насыщения материала, при дальнейшем увеличении напряженности магнитного поля магнитная индукция почти не меняется. При уменьшении напряженности намагничивающего поля кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса. Явление гистерезиса заключается в том, что изменение магнитной индукции запаздывает от изменения намагничивающего поля. Кривая зависимости B(H), получающаяся при циклическом перемагничивании ферромагнитного материала, называется петлей гистерезиса. Эта кривая изображена на рис. Чем больше площадь петли, тем больше потери на перемагничивание, нагревающие материал.
магнитная индукция быстро возрастает. Затем, из-за насыщения материала, при дальнейшем увеличении напряженности магнитного поля магнитная индукция почти не меняется. При уменьшении напряженности намагничивающего поля кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса. Явление гистерезиса заключается в том, что изменение магнитной индукции запаздывает от изменения намагничивающего поля. Кривая зависимости B(H), получающаяся при циклическом перемагничивании ферромагнитного материала, называется петлей гистерезиса. Эта кривая изображена на рис. Чем больше площадь петли, тем больше потери на перемагничивание, нагревающие материал. , где F - магнитодвижущая сила.
, где F - магнитодвижущая сила.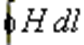 заменяют суммой
заменяют суммой 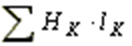 и выбирают отдельные участки магнитной цепи таким образом, чтобы H1, H2… вдоль этих участков можно было считать приблизительно постоянными.
и выбирают отдельные участки магнитной цепи таким образом, чтобы H1, H2… вдоль этих участков можно было считать приблизительно постоянными.


