
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последовательно соединенные элементов в цепи синусоидальн токаСодержание книги
Поиск на нашем сайте
Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно. В схеме протекает синусоидальный ток
U = UR+UC+UL = (делаем следующую замену)
получаем = Коэффициент при мнимой части комплексного сопротивления называют реактивным сопротивлением и обозначают Х=
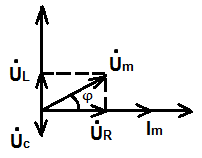
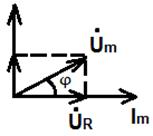
При построении векторных диаграмм цепи возник три случая. 1. XL > XC, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор ток.
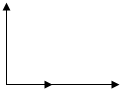 U=UR U=UR
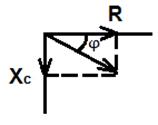
2. XL < XC Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер 3)XL = XC Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения
Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение. I = Условие возникновения резонанса: Из формулы следует, что режима резонанса можно добиться следующими способами: 1. изменением частоты; 2. изменением индуктивности; 3. изменением емкости. В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I0 (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).
24. Параллельно соединенные индуктивность, емкость К схеме подключено синусоидальное напряжение
Определим ток на входе схемы В соответствии с 1 законом Кирхгофа: Подставим формулы и получим: Где Запишем уравнение i в комплексной форме.
Активная и реактивная проводимости цепи связаны с полной проводимостью
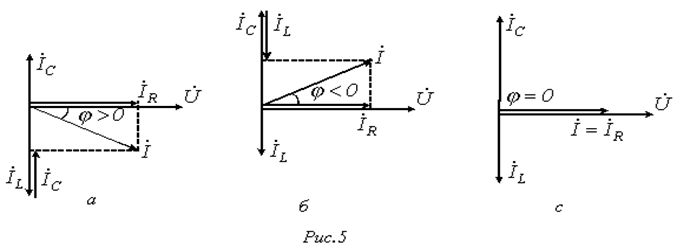
Построим векторные диаграммы, соответствующие комплексному уравнению:
В схеме на рис.5с может возникнуть режим резонанса токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы и
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.01 с.) |

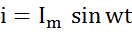
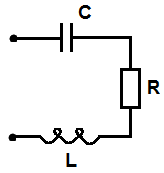 По 2-му закону Кирхгофа для мгновенного значения общее напряжение в цепи определяется как сумма мгновенных напряжений всех элементов:
По 2-му закону Кирхгофа для мгновенного значения общее напряжение в цепи определяется как сумма мгновенных напряжений всех элементов: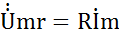 ;
; 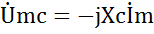 ;
; 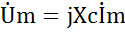
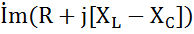
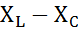 , тогда комплексное сопротивление цепи
, тогда комплексное сопротивление цепи 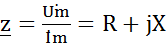
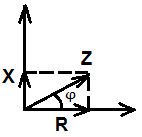
 Получаем треугольник, который называют треугольником сопротивлений и из его можно определить амплитуду и начальную фазу комплексного сопротивления z=
Получаем треугольник, который называют треугольником сопротивлений и из его можно определить амплитуду и начальную фазу комплексного сопротивления z= 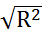 +
+ 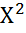
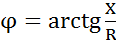 ;
;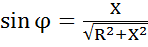 ;
; 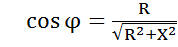
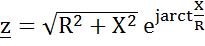
 =
= 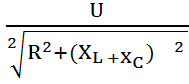
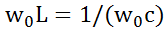 , отсюда резонансная частота равна
, отсюда резонансная частота равна 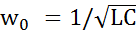
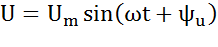
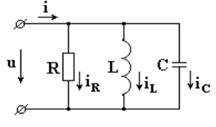 Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.
Схема состоит из параллельно включенных индуктивности, емкости и активного сопротивления.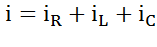 , где
, где 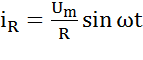 =
= 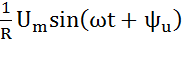 -совпадает по фазе с напряжением,
-совпадает по фазе с напряжением, 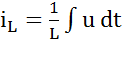 =
= 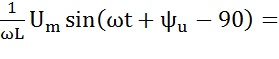
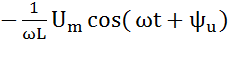 -отстает по фазе от напряжения на 90o,
-отстает по фазе от напряжения на 90o, 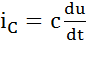 =
= 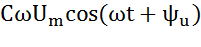 -опережает по фазе напряжение на 90o.
-опережает по фазе напряжение на 90o.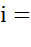
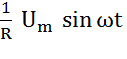 +
+ 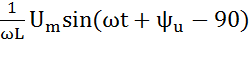 +
+ 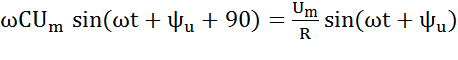 -
- 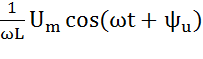 +
+ 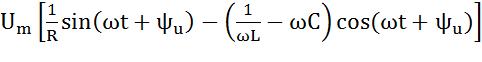 =
= 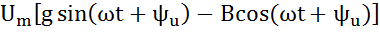 ,
,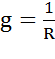 – активная проводимость, всегда положительная,
– активная проводимость, всегда положительная, 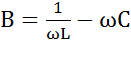 -реактивная проводимость.
-реактивная проводимость. 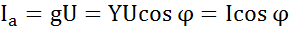 –активная составляющая тока,
–активная составляющая тока, 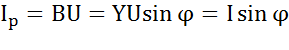 - реактивная составляющая тока.
- реактивная составляющая тока. 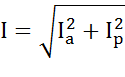
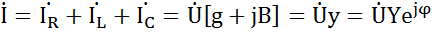 , где
, где 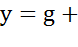 -комплексная проводимость;
-комплексная проводимость; 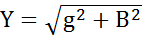 –полная проводимость, обратная полному сопротивлению
–полная проводимость, обратная полному сопротивлению 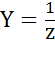 ;
; 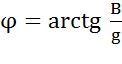 -угол разности фаз определяется по оси
-угол разности фаз определяется по оси 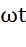 в направлении от напряжения к току и является острым или прямым.
в направлении от напряжения к току и является острым или прямым.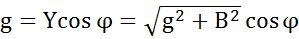
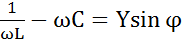
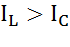 ,
, 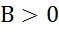
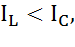
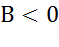
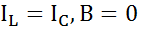
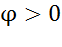 ,то цепь имеет индуктивный характер. Рис.5а
,то цепь имеет индуктивный характер. Рис.5а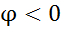 , то емкостной характер.Рис.5б
, то емкостной характер.Рис.5б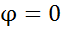 . При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.
. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением.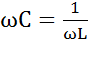 получим формулу для резонансной частоты тока
получим формулу для резонансной частоты тока 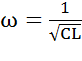 . В режиме резонанса тока полная проводимость цепи
. В режиме резонанса тока полная проводимость цепи 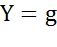 - минимальна, а полное сопротивление
- минимальна, а полное сопротивление 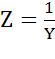 - максимально. Ток в неразветвленной части схемы
- максимально. Ток в неразветвленной части схемы 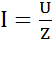 в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0,
в резонансном режиме имеет минимальное значение. В идеализированном случае R = 0, 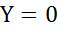 и
и 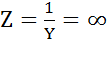 . Ток в неразветвленной части цепи
. Ток в неразветвленной части цепи 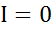 . Такая схема называется фильтр - пробкой.
. Такая схема называется фильтр - пробкой.


