Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Кирхгофа и потенциальная диаграмма.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
БАЛАНС МОЩНОСТЕЙ Целью работы является экспериментальная проверка законов Кирхгофа, баланса мощностей, а также исследование распределения электрических потенциалов вдоль контура электрической цепи. Основные теоретические положения По первому закону Кирхгофа алгебраическая сумма токов в ветвях, сходящихся в любом узле электрической цепи, равна нулю,
По второму закону Кирхгофа в любом замкнутом контуре электрической цепи алгебраическая сумма падений напряжений равна алгебраической сумме э. д. с.
Второй закон Кирхгофа наглядно иллюстрируется потенциальной диаграммой — графиком распределения потенциалов вдоль замкнутого контура электрической цепи. При построении потенциальной диаграммы по оси абсцисс откладываются последовательно одно за другим по направлению обхода контура сопротивления участков контура, а по оси ординат — потенциалы промежуточных точек этого контура, соответствующие зажимам сопротивлений. Нанесенные таким образом точки соединяют прямыми линиями. Полученный график изменения потенциала и называется потенциальной диаграммой. Внутреннее сопротивление источника энергии определяется по формуле, R0=E-U/I.
где Е — э. д. с. источника, равная напряжению на зажимах источника в режиме холостого хода; U — напряжение на зажимах источника при работе на внешнюю цепь с током I. По условию баланса мощностей в электрической цепи алгебраическая сумма мощностей источников энергии равна арифметической сумме мощностей потребителей энергии
Исследуемая электрическая цепь Работа выполняется на универсальном стенде постоянного тока. Принципиальная схема исследуемой электрической цепи показана на рис. 2.1. Измерения напряжений и потенциалов точек выполняются одним вольтметром, поочередно подключаемым к исследуемым участкам цепи. Измерение токов производится амперметрами, которые - остаются включенными в цепь в течение всего исследования.
Рис. 2.1
Подготовка к работе 1. Составить систему независимых уравнений по законам Кирхгофа для схемы, изображенной на рис. 2.1. 2. Для внешнего контура этой же схемы построить качественно потенциальную диаграмму, приняв по заданию преподавателя потенциал одной точки равным нулю. Порядок выполнения работы 1. По схеме рис. 2.2 измерить э. д. с. источников напряжения. Результаты занести в табл. 2.1. Измерения э. д. с. проводятся вольтметром. При этом предполагается, что внутреннее сопротивление вольтметра бесконечно велико и этим обеспечивается режим холостого хода источника напряжения.
рис. 2.2
2. Собрать электрическую цепь по рис. 2.1. Установить величины сопротивлений цепи таким образом, чтобы во всех ветвях цепи получить токи, достаточные для измерений. Измерить токи и напряжения на всех участках цепи. Результаты измерений занести в табл. 2.1. Таблица 2.1
3. Принять потенциал одной точки цепи равным нулю, т. е. считать условно заземленной одну точку исследуемой цепи (по указанию преподавателя). Измерить потенциалы остальных точек цепи. Результаты измерений занести в табл. 2.2. 4. Повторить измерения при условном заземлении (по указанию преподавателя) другой точки электрической цепи. Результаты измерений занести в табл. 2.2.
Таблица 2.2
Примечание. Измерения потенциалов производить вольтметром. При этом отрицательный зажим вольтметра подключается к точке с нулевым потенциалом, а положительный — поочередно прикладывается к остальным точкам цепи. Если в ходе измерений стрелка вольтметра отклоняется влево, то необходимо поменять местами зажимы вольтметра, а его показание записать с отрицательным знаком. При измерении потенциала очередной точки необходимо вернуться к исходной полярности вольтметра и т. д. Обработка полученных результатов, содержание отчета 1. На основании опытных данных (см. табл. 2.1) определить внутренние сопротивления источников энергии и сопротивления всех участников цепи. Результаты занести в табл. 2.3.
Таблица 2.3
2. По данным табл. 2.2. и 2.3 построить потенциальную диаграмму при условном заземлении одной точки исследуемой электрической цепи (см. первый опыт; табл. 2.2.). Проанализировать влияние «заземления» другой точки цепи на вид потенциальной диаграммы. 3. По данным табл. 2.1 выполнить проверку: а) первого закона Кирхгофа; б) второго закона Кирхгофа для замкнутых контуров исследуемой цепи. 4. По данным табл. 2.1 и 2.3 выполнить проверку баланса мощностей для исследуемой цепи. Результаты занести в табл. 2.4. Таблица 2.4
5. Проанализировать результаты опытов, расчетов и графических построений и сопоставить их с теоретическими положениями. 6. Оформить отчет и сделать краткие выводы по работе.
СПИСОК ЛИТЕРАТУРЫ 1. Атабеков Г. И. ТОЭ, ч. I, M., 1978, с. 45-49. 2. Зевеке Г. В. и др. Основы теории цепей. М., 1975, с. 20-21, 23-32 3. Бессонов Л. А. ТОЭ. М., 1978, с. 10—14. Работа № 3 ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА НЕКОТОРЫХ МЕТОДОВ РАСЧЕТА ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Целью работы является экспериментальная проверка метода узловых потенциалов, метода контурных токов, принципа и метода наложения и принципа взаимности, расчет на основании экспериментальных данных входных и взаимных проводимостей и передаточных коэффициентов по напряжению ветвей электрической цепи, экспериментальная проверка линейных соотношений в линейной электрической цепи. Основные теоретические положения Метод узловых потенциалов
Этот метод является одним из основных методов расчета электрических цепей. Метод можно разбить на 2 этапа. На первом этапе потенциал одного из узлов электрической цепи (для определенности – узла с наибольшим порядковым номером
где коэффициенты На втором этапе по найденным из решения системы потенциалам узлов с учетом Для цепи с тремя узлами стандартная система уравнений метода узловых потенциалов состоит из двух уравнений, каждое из которых содержит по два слагаемых.
Метод контурных токов
В методе контурных токов вначале вычисляют некоторые расчетные, так называемые «контурные» токи Порядок стандартной системы уравнений, решаемой в этом методе, равен количеству независимых контуров схемы, не содержащих источников тока.
Контура называют независимыми, если при их выборе выполняются следующие правила: в схеме не остается ни одной ветви, не вошедшей хотя бы в один контур, каждый последующий контур отличается от всех предыдущих хотя бы одной новой ветвью. Для
где Для схемы с тремя независимыми контурами стандартная система уравнений метода контурных токов содержит три уравнения, в каждом из которых по три слагаемых.
Принцип наложения и метод наложения
Принцип наложения для линейных электрических цепей заключается в следующем. Ток
При расчете (определении) токов (и/или напряжений) методом наложения, основанном на сформулированном выше принципе, поступают следующим образом: поочередно находят частичные токи Определение частичных токов (напряжений) в общем случае ведется с использованием При представлении реальных источников электроэнергии схемами замещения, содержащими идеализированные источники электроэнергии - источники ЭДС или источники тока - следует помнить, что внутреннее сопротивление источника ЭДС равно нулю, а внутреннее сопротивление источника тока бесконечно велико, поэтому при замене идеализированных источников ЭДС и тока их внутренними сопротивлениями вместо первых в схему следует включать перемычки (обладающие нулевыми сопротивлениями), а вторые заменять разрывами.
Входные и взаимные проводимости ветвей
Взаимная проводимость между двумя любыми
где По аналогии входная проводимость
где Входные и взаимные проводимости ветвей электрической цепи могут быть определены экспериментально или найдены расчетным путем. Во втором случае удобно применять метод контурных токов. При этом токи в ветвях, входные и взаимные проводимости которых рассчитываются, следует направить по ЭДС ветвей (если такие ЭДС присутствуют в схеме), выбирая независимые контура, каждую из таких ветвей включить только в один контур (первую – в первый, вторую – во второй, третью – в третий и т.д.), приравняв токи в ветвях к соответствующим контурным токам. Тогда для проводимостей будет верно:
Рассчитанные по последней формуле взаимные проводимости могут получиться либо положительными, либо отрицательными. Отрицательный знак означает, что ЭДС Проводимости
Передаточные коэффициенты ветвей по напряжению
Передаточный коэффициент по напряжению между
где
Передаточные коэффициенты по току
Аналогично определяются передаточные коэффициенты по току между
где Коэффициенты данного вида в работе не исследуются.
Принцип взаимности
В любой линейной электрической цепи ток в
Поэтому для взаимных проводимостей ветвей верно:
Линейные соотношения в электрических цепях
Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной ветви, то две любые величины (токи и напряжения двух любых ветвей) связаны между собой линейной зависимостью вида:
где роль Коэффициенты При их опытном определении достаточно знать значения двух входящих в уравнение величин (токов, напряжений) при двух различных режимах работы системы и, подставив каждую пару значений в уравнение В данной работе предлагается проверить выполнение линейных соотношений при изменении ЭДС одного из источников электроэнергии.
Исследуемая электрическая цепь
Принципиальная схема исследуемой электрической цепи приведена на рис.3.1. Используемые в работе источники электроэнергии с ЭДС Включение источников в цепь производится переключателями В варианте схемы, изображенном на рис.3.1, вместо источников ЭДС в схему введены перемычки, имитирующие нулевые сопротивления этих источников.
Рис. 3.1.
Подготовка к работе 1. Начертить частичные схемы, используемые для определения частичных токов (частичных напряжений) на участках исследуемой электрической цепи. Привести формулы для расчета токов 2. Записать выражение для определения тока 3. Записать для схемы рис.3.1 (с подключенными источниками ЭДС 4. Определить количество независимых контуров в схеме рис.3.1. Выбрать эти контура так, чтобы первая, вторая и третья ветви схемы вошли каждая только в один контур (первая – в первый, вторая – во второй и третья – в третий). Присвоить контурным токам направления, совпадающие с направлениями действия ЭДС в соответствующих ветвях. Записать для цепи стандартную систему уравнений метода контурных токов. Привести формулы для расчета параметров
Порядок выполнения работы 1. Не собирая схемы рис.1, поочередно подключить вольтметр к зажимам первого и второго источников электроэнергии и измерить ЭДС
Таблица 3.1
Собрать электрическую цепь по схеме рис.3.1, используя резисторы, сопротивления которых соответствуют заданным преподавателем величинам. Определяя полярность включения измерительных приборов, считать, что положительные направления токов в ветвях, содержащих источники электроэнергии, совпадают с направлением действия ЭДС, а вольтметрами измеряются потенциалы первого и второго узлов схемы относительно третьего узла, потенциал которого условно принят нулевым. После проверки правильности сборки цепи преподавателем подать на стенд электропитание, переключателями Измерить токи 2. Переключателями Таблица 3.2.
3. В цепи, собранной по схеме рис. 3.1, при трех включенных источниках энергии несколько (6-8) раз изменить величину ЭДС
Таблица 3.3
4. Показать полученные экспериментальные данные преподавателю и, после получения его разрешения на разборку цепи, отключить питание и разобрать ее.
Обработка полученных результатов, содержание отчета 1. По измеренным во втором опыте потенциалам узлов рассчитать напряжения на зажимах первой, второй и третьей ветвей схемы ( Результаты занести в табл.3.1. 2. Рассчитать и занести в табл.3.2 частичные напряжения Посчитать и занести в эту же таблицу алгебраические суммы частичных токов Сравнить результаты с данными табл.3.1. Убедиться в справедливости принципа наложения. 3. Используя данные табл.3.2, сравнить величины частичных токов Сделать вывод о выполнении (невыполнении) принципа взаимности. 4. На основании данных табл.3.2 рассчитать входные и взаимные проводимости ветвей. Результаты занести в первую свободную строку табл.3.4.1.
Таблица 3.4.1.
Сравнить значения Объяснить причину замеченной закономерности. Примечание по п.4. Преподаватель может предложить студентам рассчитать входные и взаимные проводимости ветвей с использованием главного определителя и алгебраических дополнений стандартной системы уравнений метода контурных токов. В этом случае расчеты удобнее провести после выполнения п.8 данного раздела. Для записи полученных результатов предназначена вторая свободная строка табл.3.4.1. 5. Используя данные табл.3.2, определить передаточные коэффициенты по напряжению между первой, второй и третьей ветвями исследуемой электрической цепи. В качестве напряжений на зажимах первой, второй и третьей ветвей следует взять напряжения
Таблица 3.4.2.
|

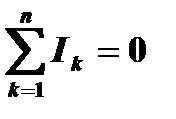


 ) принимают равным нулю, а для нахождения потенциалов остальных
) принимают равным нулю, а для нахождения потенциалов остальных 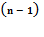 узлов записывают и решают стандартную систему уравнений следующего вида:
узлов записывают и решают стандартную систему уравнений следующего вида:
 и
и 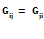 , называемые собственными
, называемые собственными  взаимными
взаимными  узловыми проводимостями, соответственно равны: первая – сумме проводимостей всех ветвей электрической цепи, сходящихся в
узловыми проводимостями, соответственно равны: первая – сумме проводимостей всех ветвей электрической цепи, сходящихся в  узле, а вторая – взятой со знаком минус сумме проводимостей всех ветвей, напрямую соединяющих
узле, а вторая – взятой со знаком минус сумме проводимостей всех ветвей, напрямую соединяющих  и
и  узлы, а так называемые расчетные узловые токи
узлы, а так называемые расчетные узловые токи  равны алгебраической сумме токов короткого замыкания всех ветвей, сходящихся в
равны алгебраической сумме токов короткого замыкания всех ветвей, сходящихся в 
 по закону Ома (в том числе для ветвей, содержащих источники ЭДС) рассчитывают токи в ветвях цепи.
по закону Ома (в том числе для ветвей, содержащих источники ЭДС) рассчитывают токи в ветвях цепи. , после чего путем алгебраического суммирования соответствующих контурных токов рассчитывают реальные токи в ветвях электрической цепи.
, после чего путем алгебраического суммирования соответствующих контурных токов рассчитывают реальные токи в ветвях электрической цепи.
 – полное (или собственное) сопротивление
– полное (или собственное) сопротивление  контура, равное сумме сопротивлений всех ветвей, образующих этот контур,
контура, равное сумме сопротивлений всех ветвей, образующих этот контур,  сопротивление смежной ветви (смежных ветвей) между
сопротивление смежной ветви (смежных ветвей) между  и
и 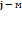 контурами (смежными называются ветви, вошедшие в состав обоих рассматриваемых контуров), равное алгебраической сумме сопротивлений этих ветвей (сумма берется положительной, если контурные токи
контурами (смежными называются ветви, вошедшие в состав обоих рассматриваемых контуров), равное алгебраической сумме сопротивлений этих ветвей (сумма берется положительной, если контурные токи  и
и  в смежных ветвях совпадают по направлению, или отрицательной, если нет), а
в смежных ветвях совпадают по направлению, или отрицательной, если нет), а  полная (контурная) ЭДС
полная (контурная) ЭДС  (напряжение
(напряжение  ) на любом
) на любом  участке цепи, в которой одновременно действуют несколько независимых источников электроэнергии, равен алгебраической сумме частичных токов
участке цепи, в которой одновременно действуют несколько независимых источников электроэнергии, равен алгебраической сумме частичных токов  (напряжений
(напряжений  ), вызываемых на этом участке каждым из источников в отдельности (
), вызываемых на этом участке каждым из источников в отдельности ( - порядковый номер источника,
- порядковый номер источника,  - их количество):
- их количество):
 (частичные напряжения
(частичные напряжения  ), вызываемые на соответствующих участках цепи каждым из
), вызываемые на соответствующих участках цепи каждым из  источников в отдельности, после чего, суммируя частичные токи (частичные напряжения) алгебраически, находят действительные токи
источников в отдельности, после чего, суммируя частичные токи (частичные напряжения) алгебраически, находят действительные токи  (напряжения
(напряжения  частичных схем, в каждой из которых на своем месте оставляется только один,
частичных схем, в каждой из которых на своем месте оставляется только один, 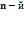 , источник электроэнергии, а все остальные источники исходной схемы заменяются их внутренними сопротивлениями.
, источник электроэнергии, а все остальные источники исходной схемы заменяются их внутренними сопротивлениями.
 ветвями линейной электрической цепи по определению равна:
ветвями линейной электрической цепи по определению равна: ,
, частичный ток в
частичный ток в 
 источника, входящего в состав
источника, входящего в состав 
 источник в
источник в  должен быть единственным в цепи).
должен быть единственным в цепи). любой
любой 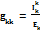 ,
, частичный ток в
частичный ток в  источника, входящего в эту же,
источника, входящего в эту же,  ветвь (при условии, что других источников энергии в цепи нет).
ветвь (при условии, что других источников энергии в цепи нет).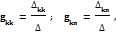
 - главный определитель стандартной системы уравнений метода контурных токов, а
- главный определитель стандартной системы уравнений метода контурных токов, а  – соответствующие алгебраические дополнения.
– соответствующие алгебраические дополнения. направленная по контурному току в
направленная по контурному току в  определяются структурой цепи и сопротивлениями ветвей и не зависят от параметров и мест включения источников электроэнергии, так как от этого не зависят определитель
определяются структурой цепи и сопротивлениями ветвей и не зависят от параметров и мест включения источников электроэнергии, так как от этого не зависят определитель  и алгебраические дополнения
и алгебраические дополнения 
 и
и  ,
, номер ветви, в которую включен единственный для схемы источник электроэнергии с ЭДС
номер ветви, в которую включен единственный для схемы источник электроэнергии с ЭДС  номер ветви, на зажимах которой замеряется напряжение
номер ветви, на зажимах которой замеряется напряжение 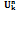 , вызванное действием этого источника.
, вызванное действием этого источника.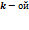 и
и 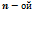 ветвями:
ветвями: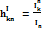 ,
, , введенного в состав
, введенного в состав 

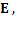 входящей в состав
входящей в состав 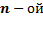 ветви, будет равен току в
ветви, будет равен току в  , включенной в
, включенной в 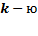
 .
.
 выполняет ток или напряжение одной ветви, роль
выполняет ток или напряжение одной ветви, роль  - ток или напряжение другой ветви.
- ток или напряжение другой ветви. и
и  могут быть найдены как расчетным, так и опытным путем.
могут быть найдены как расчетным, так и опытным путем. , решить полученную систему из двух уравнений относительно двух неизвестных
, решить полученную систему из двух уравнений относительно двух неизвестных 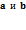 .
.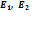 и
и  обладают ничтожно малыми внутренними сопротивлениями (в виду их малости эти сопротивления вообще не показаны на схеме). Это позволяет с достаточной степенью точности заменить реальные источники энергии идеализированными источниками ЭДС с нулевыми внутренними сопротивлениями.
обладают ничтожно малыми внутренними сопротивлениями (в виду их малости эти сопротивления вообще не показаны на схеме). Это позволяет с достаточной степенью точности заменить реальные источники энергии идеализированными источниками ЭДС с нулевыми внутренними сопротивлениями.
 в ветвях схемы рис.3.1 по известным частичным токам.
в ветвях схемы рис.3.1 по известным частичным токам. вызываемого одновременным действием источников ЭДС
вызываемого одновременным действием источников ЭДС  , использовав понятие входных и взаимных проводимостей.
, использовав понятие входных и взаимных проводимостей. . Привести формулы для расчета параметров
. Привести формулы для расчета параметров  этих уравнений, формулы для расчета токов в ветвях по известным потенциалам узлов
этих уравнений, формулы для расчета токов в ветвях по известным потенциалам узлов  .
. всех уравнений системы, формулы для расчета токов в ветвях по известным контурным токам.
всех уравнений системы, формулы для расчета токов в ветвях по известным контурным токам. и
и  этих источников; убедиться, что значения ЭДС с достаточной степенью точности соответствуют указанным на стенде величинам. (ЭДС источника электроэнергии равна напряжению на зажимах этого источника в режиме холостого хода). После этого подключить вольтметр к зажимам третьего (регулируемого) источника электроэнергии и выставить значение его ЭДС
этих источников; убедиться, что значения ЭДС с достаточной степенью точности соответствуют указанным на стенде величинам. (ЭДС источника электроэнергии равна напряжению на зажимах этого источника в режиме холостого хода). После этого подключить вольтметр к зажимам третьего (регулируемого) источника электроэнергии и выставить значение его ЭДС  , заданное преподавателем
, заданное преподавателем  Результаты измерений занести в табл. 3.1 (опыт 1).
Результаты измерений занести в табл. 3.1 (опыт 1).
 ввести в первую, вторую и третью ветви схемы источники ЭДС
ввести в первую, вторую и третью ветви схемы источники ЭДС 
 и потенциалы
и потенциалы  при одновременном действии всех трех источников. Результаты измерений занести в табл. 3.1 (опыт 2).
при одновременном действии всех трех источников. Результаты измерений занести в табл. 3.1 (опыт 2). поочередно получить из схемы рис.3.1 три частичных схемы, в каждой из которых оставлено только по одному источнику. В каждой из этих схем измерить токи в первой, второй и третьей ветвях и потенциалы первого и второго узлов (относительно третьего узла, потенциал которого считается нулевым). Результаты измерений занести в табл.3.2.
поочередно получить из схемы рис.3.1 три частичных схемы, в каждой из которых оставлено только по одному источнику. В каждой из этих схем измерить токи в первой, второй и третьей ветвях и потенциалы первого и второго узлов (относительно третьего узла, потенциал которого считается нулевым). Результаты измерений занести в табл.3.2.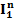







 (во всем возможном диапазоне ее изменения – от нулевого значения до наибольшего), каждый раз измеряя токи
(во всем возможном диапазоне ее изменения – от нулевого значения до наибольшего), каждый раз измеряя токи  ,
,  и потенциалы
и потенциалы  ,
,  ; результаты занести в табл. 3.3.
; результаты занести в табл. 3.3.


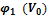
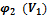

 соответственно).
соответственно). и
и  вызываемые в первой, второй и третьей ветвях схемы каждым из источников энергии в отдельности.
вызываемые в первой, второй и третьей ветвях схемы каждым из источников энергии в отдельности. и частичных напряжений
и частичных напряжений 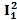 и
и 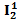 , вызываемых в первой и второй ветвях действием примерно равных по величине источников ЭДС
, вызываемых в первой и второй ветвях действием примерно равных по величине источников ЭДС  , включенных соответственно во вторую и первую ветви цепи.
, включенных соответственно во вторую и первую ветви цепи.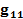
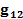


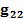
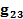





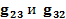 .
. и
и 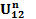 из табл.3.2. Результаты отразить в табл.3.4.2.
из табл.3.2. Результаты отразить в табл.3.4.2.