Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разветвленные цепи. Правила Кирхгофа.Содержание книги
Поиск на нашем сайте Законы Кирхгофа для разветвленной цепи (разветвленная цепь – электрическая цепь, содержащая узлы – места, где сходятся не менее трех проводников): а) По первому закону Кирхгофа – алгебраическая сумма токов, сходящихся в узле, равна нулю б) Второй закон Кирхгофа: в замкнутом контуре алгебраическая сумма произведений токов в участках на сопротивление этих участков равна алгебраической сумме электродвижущих сил, включенных в данный контур
где При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1. Выбрать произвольное направление токов на всех участках цепи. 2. Выбрать направление обхода контура; произведение 3. Составить столько уравнений, чтобы их число было равно числу неизвестных электрических величин; каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержавшийся в предыдущих контурах.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
Например, для рис. 148 первое правило Кирхгофа запишется так:
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными. Второе правило Кирхгофа получается из обобщенного закона Ома для разветвленных цепей. Рассмотрим контур, состоящий из трех участков (рис. 149). Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники тока считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам закон Ома (100.3), можно записать:
Складывая почленно эти уравнения, получим
Уравнение (101.1) выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивления Ri соответствующих участков этого контура равна алгебраической сумме э.д.с., встречающихся в этом контуре:
(101.2) При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному. 2. Выбрать направление обхода контура и строго его придерживаться; произведение IR положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются положительными, против — отрицательными. 3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных. В качестве примера использования правил Кирхгофа рассмотрим схему (рис. 150) измерительного моста Уитстона. * Сопротивления R 1, R 2, R 3и R 4 образуют его «плечи». Между точками А и В моста включена батарея с э.д.с. и сопротивлением r, между точками С и D включен гальванометр с сопротивлением RG. Для узлов А, В и С, применяя первое правило Кирхгофа, получим (10 Для контуров АСВA, ACDA и CBDC, согласно второму правилу Кирхгофа, можно записать:
* Ч. Уитстон (1802—1875) — английский физик.
Если известны все сопротивления и э.д.с., то, решая полученные шесть уравнений, можно найти неизвестные токи. Изменяя известные сопротивления R 2, R 3 и R 4, можно добиться того, чтобы ток через гальванометр был равен нулю (IG = 0). Тогда из (101.3) найдем
а из (101.4) получим
Из (101.5) и (101.6) вытекает, что
Таким образом, в случае равновесного моста (IG = 0) при определении искомого сопротивления R 1 э.д.с. батареи, сопротивления батареи и гальванометра роли не играют. На практике обычно используется реохордный мост Уитстона (рис. 151), где сопротивления R 3и R 4 представляют собой длинную однородную проволоку (реохорд) с большим удельным сопротивлением, так что отношение R 3 /R 4 можно заменить отношением l 3/ l 4. Тогда, используя выражение (101.7), можно записать
Длины l 3 и l 4 легко измеряются по шкале, a R 2 всегда известно. Поэтому уравнение (101.8) позволяет определить неизвестное сопротивление R 1.
РАЗВЕТВЛЕННЫЕ ЦЕПИ Параллельное соединение приемников. Вначале рассмотрим графоаналитический метод расчета цепи с параллельным соединением потребителей (рис. 2.16, а). Для такой цепи характерно то, что напряжения на каждой ветви одинаковы, общий ток равен сумме токов ветвей. Ток в каждой ветви определяется по закону Ома:
Угол сдвига φ между током каждой ветви и напряжением определяют с помощью cos φ:
Общий ток в цепи, как следует из первого закона Кирхгофа, равен геометрической сумме токов всех ветвей: Ī = Ī 1 + Ī 2 + Ī 3. Значение общего тока определяют графически по векторной диаграмме рис. 2.16, б. Активная мощность цепи равна арифметической сумме активных мощностей всех ветвей: Р = Р 1 + P 2 + P 3. Реактивная мощность цепи равна алгебраической сумме реактивных мощностей всех ветвей:
причем реактивную мощность ветви с индуктивностью берут со знаком плюс, ветви с емкостью — со знаком минус. Для цепи рис. 2.16 реактивная мощность равна Q = QL 1 - QC 2 + QL 3 - QC 3. Полная мощность цепи S = √ P 2 + Q 2. Угол сдвига φ между общим током и напряжением определяют из векторной диаграммы или из выражения: cos φ = P/S. Графоаналитический метод не удобен для расчета разветвленных цепей: он отличается громоздкостью и невысокой степенью точности. Для анализа и расчета разветвленных цепей переменного тока используют проводимости, с помощью которых разветвленную цепь можно преобразовать в простейшую цепь и аналитически рассчитать токи и напряжения всех ее участков. В цепях постоянного тока проводимостью называется величина, обратная сопротивлению участка цепи: g = 1/ r и ток в цепи выражается как произведение напряжения на проводимость: I = Ug.
В цепях переменного тока существуют три проводимости — полная, активная и реактивная, причем только полная проводимость является величиной, обратной полному сопротивлению последовательного участка цепи. Выражения проводимостей в цепях переменного тока можно получить следующим образом. Ток в каждом неразветвленном участке цепи раскладывают на две составляющие, одна из которых есть проекция на вектор напряжения (активная составляющая тока I a), а другая - на линию, перпендикулярную вектору напряжения (реактивная составляющая тока I р). Активная составляющая тока определяет активную мощность P = UI cos φ = UI a ; реактивная составляющая тока - реактивную мощность Q = UI sin φ = UI р. Из векторной диаграммы цепи рис. 2.17, а, изображенной на рис. 2.17, б, следует, что активная составляющая тока I 1 равна
Величина g 1 = r 1 /z 12 называется активной проводимостью ветви. Реактивная составляющая тока I 1 равна
Величина b 1 = xL/z 12 = bL 1 называется реактивной проводимостью ветви цепи с индуктивностью и в общем случае обозначается bL. Аналогично определяют активную g 2 и реактивную b 2 проводимости второй ветви цепи: I 2а = I 2cos φ2 = U/z 2 • r 2 /z 2 = Ug 2; g 2 =r 2 /z 22; I 2p = I 2 sin φ2 = U/z 2• xC /z 2 = Ub 2; b 2 = bC 2 = xC 2 /z 22. Реактивная проводимость ветви с емкостью в общем случае обозначается bC. Вектор тока первой ветви равен геометрической сумме векторов активной и реактивной составляющих тока Ī 1 = Ī 1а + Ī 1р, а значение тока I 1 = √ I 1а2 + I 1р2. Выразив составляющие тока через напряжение и проводимости, получим I 1 = √(Ug 1)2 + (UbL 1)2 = U √ g 12 + bL 12 = Uу 1 = U/z 1, где у 1 = 1 /z 1 = √ g 12 + bL 12 — полная проводимость ветви. Аналогично определяют и полную проводимость второй ветви: у 2 = 1 /z 2 = √ g 22 + bС 2. Эквивалентные активную, реактивную и полную проводимости цепи получают следующим образом. Вектор общего тока цепи равен геометрической сумме векторов токов Ī 1 и Ī 2: Ī = Ī 1 + Ī 2 и может быть выражен через активную и реактивную составляющие тока и эквивалентные проводимости всей цепи: Ī = Ī а + Ī р = Ūg э + Ūb э = Uу э = U/z э . Активная составляющая общего тока (см. рис. 2.17, б) равна арифметической сумме активных составляющих токов ветвей: (2.24) I а = I 1а + I 2а = Ug 1 + Ug 2 = U (g 1 + g 2) = Ug э. а реактивная составляющая - арифметической разности реактивных составляющих этих токов: (2.25) I р = I 1р + I 2р = UbL 1 - UbC 2 = U (bL 1- bC 2)= Ub э.
Из выражений (2.24) и (2.25) следует, что эквивалентная активная проводимость цепи равна арифметической сумме активных проводимостей параллельно включенных ветвей: (2.26) g э = g 1 + g 2 +... + gn, а эквивалентная реактивная проводимость — алгебраической сумме реактивных проводимостей параллельно включенных ветвей: (2.27) b э = bL 1 + bС 2 +... + bLn + bСп. При этом проводимости ветвей с индуктивным характером нагрузки берут со знаком плюс, ветвей с емкостным характером нагрузки — со знаком минус. Полная эквивалентам проводимость цепи (2.28) у э = 1/zэ = √ g э2 + b э2. По эквивалентным активной, реактивной и полной проводимостям можно определить параметры эквивалентной схемы (рис. 2.17, в) цепи. Эквивалентные активное, реактивное и полное сопротивления цепи определяют с помощью выражений z э = 1/ у э , r э = g э z э2, х э = b э z э2. Необходимо отметить, что если Σ bL > Σ bC, то эквивалентное сопротивление х э будет индуктивным, если Σ bC > Σ bL — емкостным. Смешанное соединение потребителей. Расчет цепи при смешанном соединении потребителей (рис. 2.18, а) может быть произведен путем замены ее простейшей эквивалентной цепью. Для этого вначале определяют активные, реактивные и полные проводимости параллельно включенных ветвей: g 1, g 2, b 1, b 2, у 1, у 2. Затем находят эквивалентные активную, реактивную и полную проводимости параллельного участка цепи: g э = g 1+ g 2; Далее определяют эквивалентные активное, реактивное и полное сопротивления параллельного участка цепи: r э = g э z э2; x э = b э z э2; z э = 1/ у э. В результате расчетов цепь может быть заменена эквивалентной цепью (рис. 2.18, б), где все сопротивления включены последовательно. Общие активное, реактивное и полное сопротивления цепи равны r об = r э + r. Цепь приобретает простейший вид, изображенный на рис. 2.18, в. Общий ток цепи определяют по закону Ома: I = U / z об Напряжение между точками а и b Uab = Iz э = I/у э . Токи в параллельных ветвях равны I 1 = Uab у 1, I 2 = Uab у 2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 5412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 . Токи, приходящие к узлу, считаются положительными, а токи, отходящие от узла, отрицательными.
. Токи, приходящие к узлу, считаются положительными, а токи, отходящие от узла, отрицательными.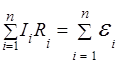 ,
,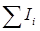 – алгебраическая сумма сил токов, сходящихся в узле;
– алгебраическая сумма сил токов, сходящихся в узле; 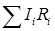 – алгебраическая сумма произведений сил токов на сопротивления замкнутых участков;
– алгебраическая сумма произведений сил токов на сопротивления замкнутых участков; 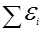 – алгебраическая сумма ЭДС источников тока на замкнутом участке цепи.
– алгебраическая сумма ЭДС источников тока на замкнутом участке цепи.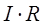 положительно, если ток на участке совпадает с направлением обхода, и, наоборот; ЭДС, действующие по выбранному направлению обхода (перемещение происходит внутри источника тока от катода к аноду), считаются положительными.
положительно, если ток на участке совпадает с направлением обхода, и, наоборот; ЭДС, действующие по выбранному направлению обхода (перемещение происходит внутри источника тока от катода к аноду), считаются положительными.
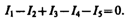


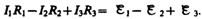 (101.1)
(101.1)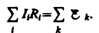
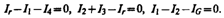 1.3)
1.3)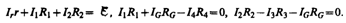 (101.4)
(101.4)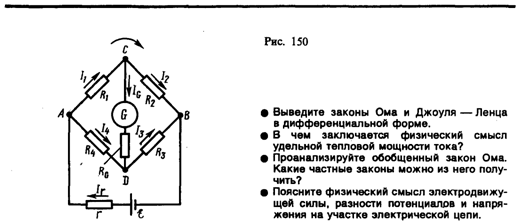
 (101.5)
(101.5) (101.6)
(101.6) (101.7)
(101.7)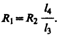 (101. 8)
(101. 8) Рис. 2.16. Цепь с параллельным соединением потребителей (а) и ее векторная диаграмма (б)
Рис. 2.16. Цепь с параллельным соединением потребителей (а) и ее векторная диаграмма (б)