Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость. Уравнение Майера.Содержание книги
Поиск на нашем сайте
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
Размерность теплоемкости: [ C ] = Дж/К. Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости. Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [ Cуд ] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Cμ - количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
[Cμ] = Дж/(моль*К). Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV. СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что Теплоемкость при постоянном объёме будет равна:
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
Из основного уравнения молекулярно-кинетической теории
Это уравнение Майера для одного моля газа. Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж. Полезно знать формулу Майера для удельных теплоёмкостей:
или
Второе начало термодинамики. Энтропия.Статистическое толкование энтропии. Связь с термодинамической вероятностью.
Самопроизвольный процесс – процесс, который может протекать без затраты работы извне. Самопроизвольный процесс может протекать или обратимо, или необратимо. Вынужденный процесс – процесс, для протекания которого требуется затрата работы извне в количестве, пропорциональном производимому изменению состояния системы. Второе начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течения процесса. Далее, второе начало термодинамики дает возможность определить, какими должны быть условия, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно для решения различных задач прикладного характера. Применимо лишь к макроскопическим системам. Формулировки второго начала термодинамики: - Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (постулат Клаузиуса). - Невозможен процесс, единственным результатом которого является превращение теплоты в работу. - Невозможно построить машину, все действия которой сводились бы к производству работы за счет охлаждения теплового источника (вечный двигатель второго рода).
Величина связанной энергии тем больше, чем меньше разность температур, и при T = const тепловая машина не может производить работу. Мерой связанной энергии является новая термодинамическая функция состояния, называемая энтропией.
Если система обратимо переходит из состояния 1 в состояние 2, изменение энтропии будет равно:
Для необратимых процессов можно записать неравенства:
1) В изолированных системах самопроизвольно могут протекать только процессы, сопровождающиеся увеличением энтропии. 2) Энтропия изолированной системы не может самопроизвольно убывать. Оба этих вывода также являются формулировками второго начала термодинамики.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.224 (0.006 с.) |



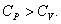 .
. ,
,
 .
.
 .
.
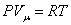 . При изобарическом процессе Р = const. Следовательно, получим:
. При изобарическом процессе Р = const. Следовательно, получим: .
.
 .
.
 .
.
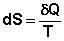 - выражение является определением новой функции состояния – энтропии и математической записью второго начала термодинамики для обратимых процессов.
- выражение является определением новой функции состояния – энтропии и математической записью второго начала термодинамики для обратимых процессов.