
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика материальной точкиСтр 1 из 13Следующая ⇒
Кинематика материальной точки Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Скорость равномерного движения определяется по формуле
где
Равноускоренным прямолинейным движением называется движение, при котором скорость
где
Перемещение, в свою очередь, равно
Также используется формула
Примером равноускоренного движения является свободное падение тела с небольшой (по сравнению с радиусом Земли) высоты h в безвоздушном пространстве. Ускорение свободного падения тела не зависит от самого тела и всегда направлено вертикально вниз. Высота тела при этом определяется формулой (при условии, что начальная скорость равна нулю). Время падения с
высоты h равно При равномерном движении со скоростью υ по окружности радиуса R ускорение (центростремительное ускорение) постоянно по модулю:
но изменяется по направлению, оставаясь все время направленным к центру окружности. Скорость материальной точки при этом все время направлена по касательной к окружности.
Период обращения T – это промежуток времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Модуль скорости движения тела при этом можно записать как
Частота обращения υ – это число оборотов, совершаемых материальной точкой при равномерном движении по окружности за единицу времени.
Часто используется понятие круговой (или циклической) частоты:
В этом случае центростремительное ускорение записывается в виде
Если модуль скорости движения материальной точки при движении по окружности изменяется, то помимо центростремительного появляется тангенциальное (касательное) ускорение a τ. Оно направлено по касательной к окружности и равно по модулю
Первый закон Ньютона
Второй закон Ньютона
Третий закон Ньютона
Выводы Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарныйимпульс: возникает закон сохранения импульса. Далее, оказывается, что многие силы вокруг нас (в частности, поле сил гравитации) обладают свойством потенциальности: работа внешних сил по переносу тела из одной точки в другую не зависит от конкретного пути (на языке математики: ротор силового поля тождественно равен нулю). В этом случае силу (векторную величину) можно представить как градиент некоторой скалярной величины — потенциала. Для того, чтобы третий закон Ньютона автоматически выполнялся, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U(| r 1- r 2|). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:
{m {v}_1^2 \over 2} + {m {v}_2^2 \over 2} + U(|{r}_1 - {r}_2|) = const. Абсолютно твердое тело Другим простейшим видом механического движения является вращательное движение материальной точки и тела. Абсолютно твердым называют тело, деформациями которого можно пренебречь, а расстояние между любыми его двумя точками сохраняется неизменным при движении. Вращательным движением абсолютно твердого тела называют движение, при котором все его точки описывают окружности, лежащие в параллельных плоскостях, а центры их лежат на оси вращения (рис. 2.1).
Угловое перемещение
Положение материальной точки при движении, например, по окружности, можно задать не только радиусом - вектором, но и угловым перемещением φ (углом поворота) радиуса - вектора, характеризующего положение м.т. относительно неподвижной плоскости Q, принятой за тело отсчета и подвижной плоскости Р, жестко связанной с вращающим телом (рис. 2.2).
Если тело совершило N оборотов, то общий угол поворота
Выражение
называют уравнением кинематики вращательного движения. Изменение углового перемещения происходит во времени и описывается по уравнению (2.2), зависит от вида вращения абсолютно твердого тела (равномерное или неравномерное вращение) с неподвижной или подвижной осями вращения. Задача кинематики: установить вид этого уравнения. При вращении абсолютно твердого тела любые его точки А и Б, находящиеся на различных расстояниях R1 и R2 от оси вращения (рис. 2.2), перемещаются с различными скоростями (v2 > v1), поэтому линейные скорости точек тела не могут характеризовать вращение тела в целом. Действительно, точки А и Б проходят различные расстояния (s2 > s1). Однако за одно и то же время Δt различные точки тела поворачиваются на один и тот же угол φ. Так как абсолютно твердое тело вращается как единое целое, то величина углового перемещения не зависит от выбора конкретной точки тела, а является характеристикой движения всего тела (рис. 2.3). Средняя угловая скорость
Пусть произвольная точка М находится в подвижной плоскости Р. Угол поворота j (угловое перемещение) всего тела и путь S будем отсчитывать от неподвижной плоскости Q по часовой стрелке (рис. 2.3).
Рис. 2.3 Угол поворота в СИ измеряется в радианах (рад). Из математики известно, что За малый промежуток времени Δt тело повернется на угол Δφ, а точка М пройдет путь по траектории
Величина радиуса R и положение центра окружности (т. 0) определяются соотношением
Разделим на Δt правую и левую части равенства (2.3):
Из кинематики поступательного движения известно, что
где <ω> - средняя угловая скорость. Средняя угловая скорость равна отношению изменения углового перемещения к промежутку времени, за которое перемещение произошло. Так как все точки тела за промежуток времени Δt поворачиваются на один и тот же угол Δφ, то средняя угловая скорость характеризует вращение тела в целом. Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул. Величина R/NА= k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле: Так как
Подставляя значение средней кинетической энергии поступательного движения молекул (31) в основное уравнение молекулярно–кинетической теории газов, получим другую форму уравнения состояния идеального газа: P = n0kT. (33) Цикл Карно
Цикл Карно состоит из четырёх стадий: 1. Изотермическое расширение (на рисунке — процесс A>Б). В начале процесса рабочее тело имеет температуру TH, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается. 2. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б>В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника. 3. Изотермическое сжатие (на рисунке — процесс В>Г). Рабочее тело, имеющее к тому времени температуру TX, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты QX. 4. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г>А). Рабочее тело отсоединяется от холодильника. При этом его температура увеличивается до температуры нагревателя.
Цикл Карно
КПД цикла Карно:
Отсюда видно, что КПД цикла Карно с идеальным газом зависит только от температуры награвателя (Tн) и холодильника (Тх). Из уравнения следуют выводы: 1. Для повышения КПД тепловой машины нужно увеличить температуру нагревателя и уменьшить температуру холодильника;
2. КПД тепловой машины всегда меньше 1. Цикл Карно обратим, так как все его составные части являются равновесными процессами.
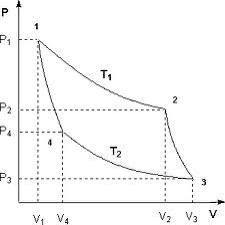
Изотермы Исследование уравнения (4) удобно производить, рассматривая изотермы Ван-дер-Ваальса. Анализируя графики
1. При высоких температурах (например, T 1, которой соответствует изотерма 1) изобара AD пересекает изотерму в одной точке. Уравнение Ван-дер-Ваальса имеет один вещественный корень, т.е. каждому значению T соответствует единственное значение объема. Из этого следует, что при высоких температурах вещество находится в однофазном – газообразном состоянии. 2. Невысоким температурам соответствуют изотермы 2, 3, 4, на которых имеются перегибы. Изобара AD пересекает изотерму 4 в трех точках А, B, C. В уравнении Ван-дер-Ваальса это состояние соответствует трём вещественным значениям объема при данных p и T. Это означает, что вещество находится в трёх фазовых состояниях. Под фазой понимают совокупность всех частей системы, обладающих одинаковыми физическими и химическими свойствами. 3. Переход изотермы 5 к изотермам 4, 3 и т. д., соответствующий повышению температуры, приводит к тому, что изгибы на изотермах сглаживаются. Расстояние, например, между точками A и C уменьшается и уже на изотерме 2 они сливаются в одну точку – точку К перегиба. В точке перегиба изобара Экспериментальные изотермы (рис. 2) могут быть получены путём сжатия газа в изотермических условиях. Экспериментальные и теоретические изотермы на участках 1 – 2 и 3 – 4 с известным приближением можно считать совпадающими. При особых условиях эксперимента могут быть получены участок 2 – 2/, соответствующий пересыщенному пару, и участок 3 – 3/, относящийся к перегретой жидкости. Это малоустойчивые, метастабильные состояния.
Метастабильным состоянием называется равновесное состояние с ограниченной устойчивостью. При отклонении от этого состояния вещество не стремится к нему обратно, а легко переходит в другое устойчивое состояние. Метастабильные состояния существуют ограниченное время. Чтобы получить такое метастабильное состояние как перегретый пар необходимо отсутствие в газе инородных и смачиваемых включений, которые являются центрами конденсации. Перегретой может быть только очень чистая жидкость, в которой нет зародышей газовой фазы. Как правило, они всегда присутствуют в виде мельчайших пузырьков на стенках сосуда, содержащего жидкость, или на взвешенных в жидкости пылинках. Вещество на участке 2 – 3 находиться в двухфазном состоянии, т. е. часть первоначального газообразного вещества превратилась в жидкость, а часть осталась в газообразном состоянии. Соответствующее участку 2 – 3 давление называется давлением насыщения. Точка 3 (рис. 2) соответствует состоянию, когда весь газ превращается в жидкость.
С ростом температуры участки, соответствующие двухфазному состоянию, становятся уже (рис. 3). Затем появляется изотерма, на которой этот участок превращается в точку перегиба К; ей соответствует критическая температура. При температурах ниже критической есть участок насыщения, и вещество может переходить из газообразного состояния в жидкое состояние (область I, рис. 3). Температурам выше критической соответствует только газообразное состояние (область II, рис. 3). Область III, примыкающая к оси ординат (рис. 3), относится к жидкому состоянию системы.
Критическая температура – это наивысшая температура, при которой газ может ещё быть превращён в жидкость. Давление и объем, соответствующие точке перегиба К, называются критическими. При критическом состоянии вещества различия в свойствах пара и жидкости отсутствуют. Критическое состояние характеризуется непрерывным переходом пара в жидкость и жидкости в пар. При этом удельная теплота парообразования и коэффициент поверхностного натяжения равны нулю. Параметры критического состояния вещества связаны с постоянными Ван-дер-Ваальса
или
Постоянный ток. Закон Ома для однородного, неоднородного участков в полной цепи. Сторонние силы, ЭДС. Электрическое сопротивление проводников. Зависимость сопротивления от температуры. Теория электронной проводимости в металлах. Постоянный ток — электрический ток, параметры, свойства и направление которого не изменяются со временем.
Плотность тока:
V – скорость движения; n – концентрация; S – площадь поперечного сечения. Простейшим источником постоянного тока является химический источник (гальванический элемент или аккумулятор), поскольку полярность такого источника не может самопроизвольно измениться. Постоянный ток широко используется в технике: подавляющее большинство электронных схем в качестве питания используют постоянный ток. Условия возникновения тока: · Свободные заряженные частицы · Разность потенциалов · Электростатическое поле Закон Ома для однородного участка цепи:
Закон Ома для неоднородного участка цепи:
ЭДС – элекро-движущая сила.
Ст – сторонняя Электрическое сопротивление проводников. Зависимость сопротивления от температуры.
𝒫 – удельное сопротивление; L – длина проводника; S – площадь поперечного сечения.
Теория электронной проводимости в металлах. Смысл электронной теории проводимости сводится к тому, что каждый атом металла отдает валентный электрон из внешней оболочки, и эти свободные электроны растекаются по металлу, образуя некое подобие отрицательно заряженного газа. Атомы металла при этом объединены в трехмерную кристаллическую решетку, которая практически не препятствует перемещению свободных электронов внутри нее. Как только к проводнику прикладывается электрическая разность потенциалов (например, посредством замыкания на два его конца двух полюсов аккумуляторной батареи), свободные электроны приходят в упорядоченное движение. Сначала они движутся равноускоренно, но длится это недолго, поскольку очень скоро электроны перестают ускоряться, сталкиваясь с атомами решетки, которые, в свою очередь, от этого начинают колебаться всё с большей амплитудой относительно условной точки покоя, и мы наблюдаем термоэлектрический эффект разогревания проводника. На электроны же эти столкновения оказывают затормаживающее воздействие, аналогично тому, как, допустим, человеку тяжело с достаточно большой скоростью передвигаться в плотной людской толпе. В результате скорость электронов устанавливается на некоей усредненной отметке, которая называется скоростью миграции, и скорость эта, на самом деле, отнюдь не высока. Например, в обычной бытовой электропроводке средняя скорость миграции электронов составляет всего несколько миллиметров в секунду, то есть, электроны отнюдь не летят по проводам, а скорее ползут по ним темпами, достойными разве что улитки. Свет же в лампочке зажигается практически моментально лишь потому, что с места все эти медлительные электроны трогаются одновременно, как только вы нажимаете на кнопку выключателя, и электроны в спирали лампочки также приходят в движение сразу же. То есть, нажимая на кнопку выключателя, вы производите в проводах эффект, аналогичный тому, как если бы включили насос, подсоединенный к поливочному шлангу, до отказа заполненному водой, — струя на противоположном от насоса конце хлынет из шланга незамедлительно. Кинематика материальной точки Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Скорость равномерного движения определяется по формуле
где
Равноускоренным прямолинейным движением называется движение, при котором скорость
где
Перемещение, в свою очередь, равно
Также используется формула
Примером равноускоренного движения является свободное падение тела с небольшой (по сравнению с радиусом Земли) высоты h в безвоздушном пространстве. Ускорение свободного падения тела не зависит от самого тела и всегда направлено вертикально вниз. Высота тела при этом определяется формулой (при условии, что начальная скорость равна нулю). Время падения с
высоты h равно При равномерном движении со скоростью υ по окружности радиуса R ускорение (центростремительное ускорение) постоянно по модулю:
но изменяется по направлению, оставаясь все время направленным к центру окружности. Скорость материальной точки при этом все время направлена по касательной к окружности.
Период обращения T – это промежуток времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Модуль скорости движения тела при этом можно записать как
Частота обращения υ – это число оборотов, совершаемых материальной точкой при равномерном движении по окружности за единицу времени.
Часто используется понятие круговой (или циклической) частоты:
В этом случае центростремительное ускорение записывается в виде
Если модуль скорости движения материальной точки при движении по окружности изменяется, то помимо центростремительного появляется тангенциальное (касательное) ускорение a τ. Оно направлено по касательной к окружности и равно по модулю
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.212 (0.07 с.) |

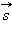 – перемещение тела за время t.
– перемещение тела за время t.
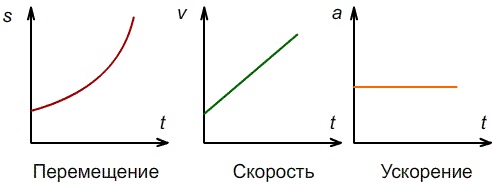
 и ускорение
и ускорение  направлены вдоль одной прямой и ускорение остается неизменным по модулю. В этом случае модуль ускорения определяется по формуле
направлены вдоль одной прямой и ускорение остается неизменным по модулю. В этом случае модуль ускорения определяется по формуле
 – изменение модуля скорости тела за время t. Таким образом, при равноускоренном прямолинейном движении скорость равна
– изменение модуля скорости тела за время t. Таким образом, при равноускоренном прямолинейном движении скорость равна
 где x 0 – значение перемещения в момент времени t = 0.
где x 0 – значение перемещения в момент времени t = 0.




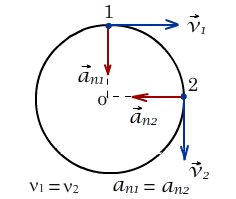



 Полное ускорение в этом случае будет равно
Полное ускорение в этом случае будет равно


 Рис. 2.2
Рис. 2.2
 Рис. 2.3
Рис. 2.3

 .
. .
. .
. Тогда
Тогда ,
,
 =
= 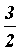 kТ, то средняя квадратичная скорость равна
kТ, то средняя квадратичная скорость равна . (32)
. (32)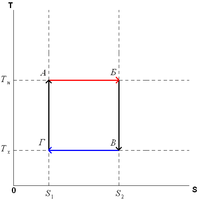
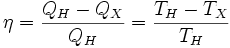
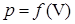 на рис. 1, можно сделать три вывода.
на рис. 1, можно сделать три вывода.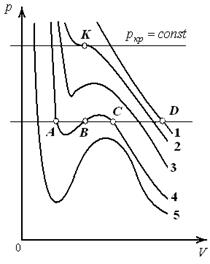
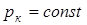 является касательной к изотерме. Температура Tк, соответствующая этой изотерме называется критической температурой.
является касательной к изотерме. Температура Tк, соответствующая этой изотерме называется критической температурой.

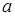 и
и  :
: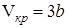 ,
, 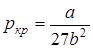 ,
,  , (5)
, (5)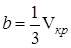 ,
, 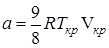 .
.
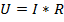





 [В]
[В]





