
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В механике введилось понятие числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения.
В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения.
Рис.1
При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> (энергия поступательного движения молекул):
В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост+iвращ+2iколеб
В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.
Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул:
Внутренняя энергия для произвольной массы m газа.
где М — молярная масса, ν — количество вещества.
Число степеней свободы тела - это сколько координат надо знать, чтобы отнгозначно описать его движение. Например, для материальной точки (имеющей нулевой размер) достаточно знать три параметра - по осям коголрдинат. Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Внутренняя энергияU - энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Внутренняя энергия -однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определенной (единственной) энергией. Внутренняя энергия не зависит от того, как система пришла в данное состояние: при переходе из состояния (1) в состояние (2) изменение внутренней энергии DU определяется только разностью значений внутренней энергии этих состояний DU = U1 - U2 и не зависит от пути перехода. Число степеней свободы системы i - это число независимых переменных (координат), полностью определяющих положение системы в пространстве: - Одноатомная молекула идеального газа имеет три степени свободы поступательного движения, т.е. i=3. - Двухатомная молекула идеального газа имеет три степени поступательного движения и две степени свободы вращательного движения, т.е. i=5. - Трехатомная молекула (и вообще нелинейная многоатомная молекула) идеального газа имеет три степени поступательного движения и три степени вращательного движения, т.е. i=6. - Для реальных молекул следует учитывать также степени свободы колебательного движения. - Независимо от числа степеней свободы молекул три степени свободы всегда поступательные; ни одна из поступательных степеней свободы не имеет преимущества перед остальными. Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень - в среднем энергия, равная kT (на колебательную степень свободы приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы). Таким образом, средняя энергия молекулы Е> = ikT/2, где i - сумма числа поступательных iпост, числа вращательных iвращ и удвоенного числа колебательных iколеб степеней свободы молекулы i = iпост + iвращ + 2iколеб. Для идеального газа i совпадает с числом степеней свободы молекулы. Внутренняя энергия 1 моль идеального газа равна сумме кинетических энергий NA молекул Um = ikTNA = iRT/2, (1a) и изменение внутренней энергии 1 моль идеального газа dUm =(iR/2)dT (1b) (молекулы между собой не взаимодействуют и поэтому взаимная потенциальная энергия молекул газа равна нулю). Внутренняя энергия произвольной массы m идеального газа U = (m/M)(iRT/2)=n(iRT/2), где М - молярная масса (масса одного моля), n = m/M - количество вещества.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 4288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.168 (0.008 с.) |


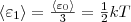
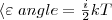
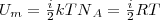 (1)
(1)



