
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число степеней свободы. Закон равномерного распределения молекул по степеням свободы молекул.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Число степеней свободы: наименьшее число независимых координат, определяющих положение и конфигурацию молекулы в пространстве. Число степеней свободы для одноатомной молекулы - 3,для двухатомной - 5, для трехатомной - 6. Теорема о распределении энергии по степеням свободы гласит: при термодинамическом равновесии кинетическая энергия в среднем равномерно распределяется по всем степеням свободы, по kT /2 на каждую степень свободы. k — константа Больцмана, T — абсолютная температура газа Внутренняя энергия системы. Первое начало термодинамики. Первое начало термодинамики
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил. Вну́тренняя эне́ргия тела— это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии. Работа, совершаемая газом при изменениях объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде. Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работу
где S — площадь поршня, Sdl=dV— изменение объема системы. Таким образом,
Полную работу А, совершаемую газом при изменении его объема от V1 до V2, найдем интегрированием формулы:
Внутренняя энергия и теплоемкость идеального газа. Для идеального газа внутренняя энергия равна:
где Теплоёмкость идеального газа — отношение количества теплоты, сообщённого газу, к изменению температуры δТ, которое при этом произошло.
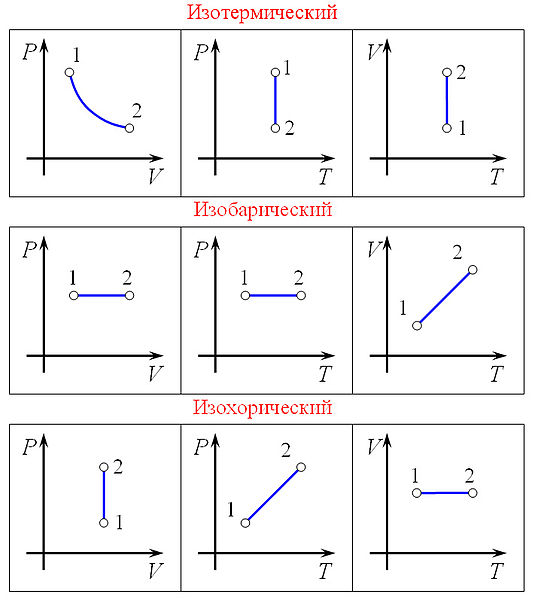
Изопроцессы. Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии —изоэнтропийный (например, обратимый адиабатический процесс).
Изобарный процесс Работа, совершаемая газом при расширении или сжатии газа, равна
Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: Изохорный процесс Из определения работы следует, что изменение работы при изохорном процессе равно:
Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:
при изохорном процессе газ работы не совершает: А=0. Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю. Изменение внутренней энергии идеального газа можно найти по формуле:
Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:
где Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:
Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:
То есть вся теплота, которую получает газ идёт на изменение его внутренней энергии. Изотермический процесс Первый закон термодинамики для изотермического процесса записывается в виде:
Изоэнтропийный процесс — процесс изменения состояния термодинамической системы при постоянной энтропии (S=const). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:
где Применение первого начала термодинамики к изопроцессам. Изобарный процесс Работа, совершаемая газом при расширении или сжатии газа, равна Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: Изохорный процесс Из определения работы следует, что изменение работы при изохорном процессе равно:
Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:
при изохорном процессе газ работы не совершает: А=0. Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю.
Изменение внутренней энергии идеального газа можно найти по формуле:
Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:
где Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:
Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 497; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.142.101 (0.011 с.) |

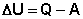

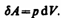

 ,
, - количество степеней свободы,
- количество степеней свободы,  - универсальная газовая постоянная.
- универсальная газовая постоянная.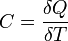
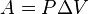 .
. .
.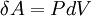
 ,
, ,
, ,
,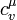 — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме.
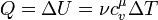 ,
,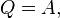

 — показатель адиабаты, определяемый типом газа.
— показатель адиабаты, определяемый типом газа.


