Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютно неупругий удар. Абсолютно упругий удар.Содержание книги
Поиск на нашем сайте
Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело. Где v это общая скорость тел, полученная после удара, ma - масса первого тела, ua - скорость первого тела до соударения. mb - масса второго тела, ub -скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно. Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соудареямых тел в результате неупругих деформаций переходит в тепловую. Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики. Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом: Есть в наличии два абсолютно твердых тела, которые сталкиваются В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию. Контакт тел прекращается и они продолжают движение. Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.
Здесь m1, m2 - массы первого и второго тел. u1, v1 - скорость первого тела до, и после взаимодействия. u2, v2 - скорость второго тела до, и после взаимодействия.
Импульсы складываются векторно, а энергии скалярно. Вращение тела вокруг неподвижной оси.
Вращением твердого тела вокруг неподвижной оси (или просто вращательным движением) называется такое движение твердого тела, при котором в теле можно выделить прямую, все точки которой будут оставаться неподвижными во время движения. Эта прямая называется осью вращения твердого тела. Кинематические характеристики Вращение характеризуется углом При равномерном вращении (T оборотов в секунду), · Частота вращения — число оборотов в единицу времени.
· Период вращения — время одного полного оборота. Период вращения T и его частота · Линейная скорость точки, находящейся на расстоянии R от оси вращения
· Угловая скорость вращения тела
Динамические характеристики Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Кинетическую энергии вращения можно записать в виде · Момент инерции механической системы относительно неподвижной оси a — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: mi — масса i -й точки, ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении. · Кинетическая энергия вращательного движения
где Jz — момент инерции тела относительно оси вращения. 14. Момент инерции тела. Расчет момента инерции некоторых тел. Момент инерции — скалярная физическая величина, численно равная произведению массы материальной точки на квадрат расстояния до оси вращения. Единица измерения СИ: кг·м².
Согласно теореме Штейнера момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.65.39 (0.01 с.) |


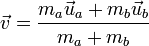
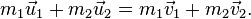

 , измеряющимся в градусах или радианах, угловой скоростью
, измеряющимся в градусах или радианах, угловой скоростью  (измеряется в рад/с) и угловым ускорением
(измеряется в рад/с) и угловым ускорением  (единица измерения — рад/с²).
(единица измерения — рад/с²). ,
, связаны соотношением
связаны соотношением  .
. ,
,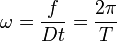 .
. . Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы  .
. ,
,
 — угловая скорость
— угловая скорость