Опытные законы идеального газа.

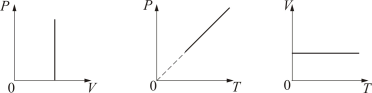
В XVII – XIX веках были сформулированы опытные законы идеальных газов.

Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.

1. Изохорический процесс. Закон Шарля. V = const.

Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:

При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.

2. Изобарический процесс. Закон Гей-Люссака. Р = const.

Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:

При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.

Уравнение изобары:

.

3. Изотермический процесс. Закон Бойля – Мариотта. T = const.

Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.

Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:

При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.

Уравнение изотермы:

 

 

4. Адиабатический процесс (изоэнтропийный):

Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.

5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.

6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится N_A =6,02·10²³ молекул (число Авогадро).

7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:

Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.

При , давление смеси газов:

8. Объединённый газовый закон (Закон Клапейрона).

29. Уравнение Клапейрона-Менделеева. Уравнение имеет вид: , где · р — давление, · — молярный объём, · R — универсальная газовая постоянная · T — абсолютная температура, К. Так как , где — количество вещества, а , где m — масса, M — молярная масса, уравнение состояния можно записать:     30. Основное уравнение молекулярно-кинетической теории идеальных газов. Основное уравнение МКТ 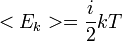, где k является постоянной Больцмана, i — число степеней свободы молекул, T - абсолютная температура. Вывод основного уравнения МКТ Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём. Обозначим скорость движения , тогда перед столкновением со стенкой сосуда импульс частицы равен , а после — , поэтому стенке передается импульс . Время, через которое частица сталкивается с одной и той же стенкой, равно . Отсюда следует: Так как давление , следовательно сила Подставив, получим: Преобразовав: Так как рассматривается кубический сосуд, то Отсюда: . Соответственно, и . Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z. Поскольку , то 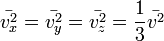. Это следует из того, что все направления движения молекул в хаотичной среде равновероятны. Отсюда или . Пусть — среднее значение кинетической энергии всех молекул, тогда: , откуда, используя то, что (количество вещества), а , имеем . 31. Закон Максвелла для распределения идеального газа по скоростям и энергиям теплового движения. Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля. Функция распределения молекул по скоростям f(v)=dN(v)/Ndv определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv и имеет смысл плотности вероятности. Для газа, подчиняющегося классической механике, в состоянии статистического равновесия функция распределения f Максвелла по скоростям имеет вид: f(v) =n(m/2pkT)^3/2exp(-mv^2/2kT), Где m — масса молекулы, Т — абсолютная температура системы, k — постоянная Больцмана. Значение функции распределения f(v) зависит от рода газа (от массы молекул) и от температуры. С помощью распределения Максвелла можно вычислять средние значения скоростей молекул и любых функций этих скоростей. В частности, средняя квадратичная скорость v^2=3kT/m, а средняя скорость молекулы v= (8kT/pm)^1/2. Распределение по энергии Наконец, используя соотношения и , мы получаем распределение по кинетической энергии: 32. Барометрическая формула. Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру Т и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид: где p — давление газа в слое, расположенном на высоте h, — давление на нулевом уровне (), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону: где m — масса молекулы газа, k — постоянная Больцмана.