Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорение и его составляющие. Угловая скорость и угловое ускорение.Содержание книги
Поиск на нашем сайте
Ускорение и его составляющие. Угловая скорость и угловое ускорение. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
3. Законы Ньютона. 1-ый. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий или когда, внешние воздействия взаимно компенсируются, сохраняет величину и направление своей скорости неограниченно долго. 2-ой. В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. Закон сохранения механической энергии может быть выведен из второго закона Ньютона, если учесть, что в консервативной системе все силы могут быть представлены в виде
где
где т — масса частицы,
8. Консервативные силы. Потенциальная энергия во внешнем поле сил. Консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0. В случае когда работа сил поля не зависит от пути, а зависит лишь от начального и конечного положений частицы, каждой точке поля можно сопоставить значение некоторой функции такой, что разность значений этой функции в точках будет определять работу сил при переходе частицы из первой точки во вторую:
Это сопоставление можно осуществить следующим образом. Некоторой исходной точке О припишем произвольное значение функции, равное. Любой другой точке Р припишем значение
где — работа, совершаемая над частицей консервативными силами при перемещении частицы из точки Р в точку О. Поскольку работа не зависит от пути, определенное таким способом значение U(Р) будет однозначным. Отметим, что функция U(Р) имеет размерность работы (или энергии). Значения функции в точках 1 и 2 равн Образуем разность этих значений Сумма дает работу, совершаемую силами поля при перемещении частицы из точки 1 в точку 2 по траектории, проходящей через точку О. Однако работа, совершаемая над частицей при ее перемещении из точки 1 в точку 2 по любой другой траектории (в том числе и не проходящей через точку О), будет такой же. Таким образом, с помощью функции U можно определять работу, совершаемую над частицей консервативными силами на любом пути, начинающемся в произвольной точке 1 и заканчивающемся в произвольной точке 2. Пусть на частицу действуют только консервативные силы.
Полученный результат означает, что величина
для частицы, находящейся в поле консервативных сил, остается постоянной.
Момент силы. Моментом силы называют вращательное усилие создаваемое вектором силы относительно другого объекта. Размерность - [Н⋅м]. Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы. Определяется как произведение силы на плечо: M(F)=F⋅h Здесь h - плечо момента, определяется как кратчайшее расстояние от точки до линии действия силы.
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соудареямых тел в результате неупругих деформаций переходит в тепловую. Динамические характеристики Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Кинетическую энергии вращения можно записать в виде · Момент инерции механической системы относительно неподвижной оси a — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: mi — масса i -й точки, ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении. · Кинетическая энергия вращательного движения
где Jz — момент инерции тела относительно оси вращения. 14. Момент инерции тела. Расчет момента инерции некоторых тел. Момент инерции — скалярная физическая величина, численно равная произведению массы материальной точки на квадрат расстояния до оси вращения. Единица измерения СИ: кг·м².
Согласно теореме Штейнера момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Гироскопы. Свободные оси. Гироско́п — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчета. Простейший пример гироскопа — юла. Существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на нее внешних сил. Эти оси называются свободными осями (или осями свободного вращения). Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот) и т. д. При всяком отклонении от курса вследствие каких-то воздействий (волны, порыва ветра и т. д.) положение оси гироскопа в пространстве сохраняется. Следовательно, ось гироскопа вместе с рамами карданова подвеса поворачивается относительно движущегося устройства. Поворот рам карданова подвеса с помощью определенных приспособлений включает рули управления, которые возвращают движение к заданному курсу.
Сила сопротивления зависит от формы тела. Придание телу специально рассчитанной обтекаемой формы существенно уменьшает силу сопротивления, так как в этом случае жидкость всюду прилегает к его поверхности и позади него не завихрена. Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории, а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее. Первое начало термодинамики
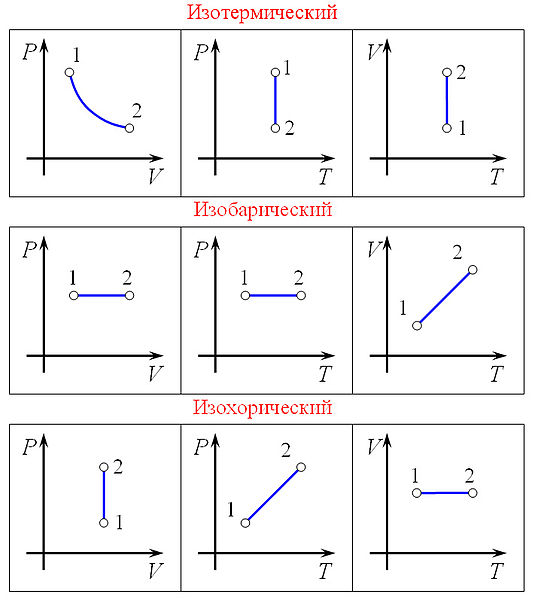
Изопроцессы. Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии —изоэнтропийный (например, обратимый адиабатический процесс).
Изобарный процесс Работа, совершаемая газом при расширении или сжатии газа, равна Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: Изохорный процесс Из определения работы следует, что изменение работы при изохорном процессе равно:
Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:
при изохорном процессе газ работы не совершает: А=0. Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю. Изменение внутренней энергии идеального газа можно найти по формуле:
Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:
где Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:
Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:
Изотермический процесс Первый закон термодинамики для изотермического процесса записывается в виде:
Изоэнтропийный процесс — процесс изменения состояния термодинамической системы при постоянной энтропии (S=const). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:
где Изобарный процесс Работа, совершаемая газом при расширении или сжатии газа, равна Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: Изохорный процесс Из определения работы следует, что изменение работы при изохорном процессе равно:
Чтобы определить полную работу процесса проинтегрируем данное выражение. Поскольку объем неизменен, то:
при изохорном процессе газ работы не совершает: А=0. Графически доказать это намного проще. С математической точки зрения, работа процесса — это площадь под графиком. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю. Изменение внутренней энергии идеального газа можно найти по формуле:
Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде:
где Используя первое начало термодинамики можно найти количество теплоты при изохорном процессе:
Но при изохорном процессе газ не выполняет работу. То есть, имеет место равенство:
Изотермический процесс Первый закон термодинамики для изотермического процесса записывается в виде:
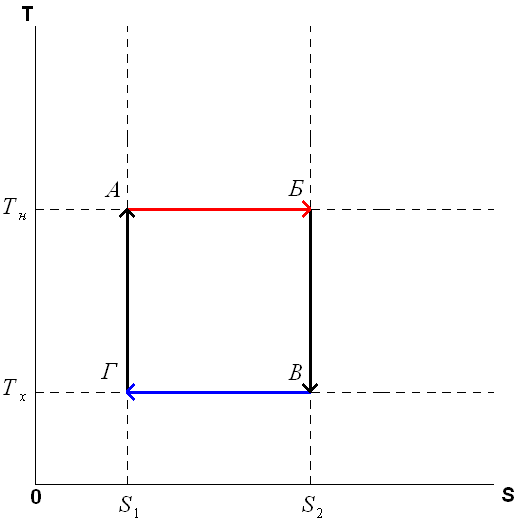
Описание цикла Карно Пусть тепловая машина состоит из нагревателя с температурой Цикл Карно состоит из четырёх стадий: 1. Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру 2. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника. 3. Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру 4. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя. При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:
КПД тепловой машины Карно Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Уравнение Ван-дер-Ваальса Уравнение состояния Для одного моля газа ур-е Ван-дер-Ваальса имеет вид:
Где p — давление, Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — объем молекул газа. Для v молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
Традиционный вывод. Рассмотрим газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет:
Стоит заметить - вычитаемый объём b не будет в точности равен суммарному объёму всех частиц. Если частицы считать твёрдыми и абсолютно упругими шариками, то вычитаемый объём будет примерно в 4 раза больше. Это объясняется тем, что центры упругих шаров не могут приближаться на расстояние ближе 2r. Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения: · Частицы распределённые равномерно по всему объёму. · Силы притяжения стенок сосуда не учитываются, что в общем случае неверно. · Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга. Таким образом, для частиц внутри сосуда силы притяжения не учитываются. А частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации: Число частиц, которые находятся непосредственно у стенок, в свою очередь тоже предполагается пропорциональным концентрации n. Можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:
И зотермы Ван-дер-Ваальса — кривые зависимости р от V m при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 89) имеют довольно своеобразный характер. При высоких температурах (T > T к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T к на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической, соответствующая ей температура T к — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V к, и давление р к называются также критическими. Состояние с критическими параметрами (p к, V к, T к) называется критическим состоянием. При низких температурах (Т < T к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь. Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса (61.2) к виду
Уравнение (62.1) при заданных р и Т является уравнением третьей степени относительно V m; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V 1, V 2 и V 3 отвечают (символ «m» для простоты опускаем) одному значению давления р 1), второму случаю — изотермы при высоких температурах. Рассматривая различные участки изотермы при T < Т к (рис. 90), видим, что на участках 1 — 3 и 5 — 7 при уменьшении объема V m давление р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7 — 6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2 – 1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Данные выводы, следующие из анализа уравнения Ван-дер-Ваальса, были подтверждены опытами ирландского ученого Т. Эндрюса. Отличие экспериментальных (Эндрюс) и теоретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во втором — волнообразные. Для нахождения критических параметров подставим их значения в уравнение (62.1) в запишем
(символ «m» для простоты опускаем). Поскольку в критической точке все три корня совпадают и равны V к уравнение приводится к виду
Tax как уравнения (62.2) и (62.3) тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р,V m под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении. Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2 — 6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5— 6 и 2 — 3. Эти неустойчивые состояния называются метастабильными. Участок 2-3 изображает перегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы. При достаточно низких температурах изотерма пересекает ось V m, переходя в область отрицательных давлений (нижняя кривая на рис. 92). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9—10 — растянутой жидкости. Или
И периодом
Формула (142.3) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (см. (21.3)), т. е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (141.5) и (142.2), равна
2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 201). Принимая
Получим уравнение
идентичное с (142.1), решение которого (140.1) известно:
Где l — длина маятника. Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив выражение (142.8) в формулу (1417), получим выражение для периода малых колебаний математического маятника
Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
Решим систему
Решение системы:
Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:
Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω Период биений:
Определение частоты тона (звука определенной высоты биений эталонным и измеряемым колебаниями — наиболее широко применяемый на метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.
Ускорение и его составляющие. Угловая скорость и угловое ускорение. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
3. Законы Ньютона. 1-ый. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий или когда, внешние воздействия взаимно компенсируются, сохраняет величину и направление своей скорости неограниченно долго. 2-ой. В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.161.41 (0.016 с.) |



 откуда
откуда Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:




 ,
, — потенциальная энергия материальной точки (
— потенциальная энергия материальной точки ( — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид
— радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид ,
, — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что
— вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что  , можно получить
, можно получить

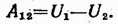






 ,
, ,М =I*E, где Е- угловое ускорение.
,М =I*E, где Е- угловое ускорение. . Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы  .
. ,
,
 — угловая скорость
— угловая скорость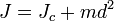
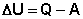
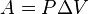 .
. .
.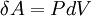
 ,
, ,
, ,
,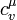 — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме.
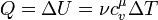 ,
,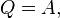

 — показатель адиабаты, определяемый типом газа.
— показатель адиабаты, определяемый типом газа. , холодильника с температурой
, холодильника с температурой  и рабочего тела.
и рабочего тела. . При этом объём рабочего тела увеличивается.
. При этом объём рабочего тела увеличивается. .
. при
при  .
.

 .
. .
. .
.
 — молярный объём, T — абсолютная температура, R — универсальная газовая постоянная.
— молярный объём, T — абсолютная температура, R — универсальная газовая постоянная. где V — объём.
где V — объём.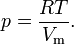 Предположим, что частицы этого газа являются упругими сферами одинакового радиуса r. Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b. Получается следующее уравнение:
Предположим, что частицы этого газа являются упругими сферами одинакового радиуса r. Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b. Получается следующее уравнение: 
 .
.
 окончательное уравнение
окончательное уравнение 48. Изотермы Ван-дер-Ваальса и их анализ.
48. Изотермы Ван-дер-Ваальса и их анализ. (62.1)
(62.1)
 (62.2)
(62.2) (62.3) или
(62.3) или
 (62.4). Решая полученные уравнения, найдем
(62.4). Решая полученные уравнения, найдем
 (141.4)
(141.4) (142.3)
(142.3)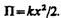
 (142.5)
(142.5)
 (142.6)
(142.6)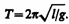 (142.9)
(142.9)