
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Ома и Кирхгофа для цепей постоянного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Законы Ома и Кирхгофа для цепей постоянного тока. Разветвленными называются цепи, содержащие узлы, т. е. точки, к которым подходит не менее трех проводников. Поскольку энергия в узлах накапливаться не может, сумма токов, притекающих в любой момент к узлу, равна сумме токов, утекающих от узла. Данное правило называется первым законом Кирхгофа. Закон, устанавливающий равенство между алгебраической суммой мгновенных значений ЭДС в замкнутом контуре и алгебраической суммой мгновенных падений напряжений на всех элементах этого же контура, называется вторым законом Кирхгофа. Расчёт электрических цепей постоянного тока методом уравнений Кирхгофа. Расчёт электрических цепей постоянного тока методом контурных токов. Расчёт электрических цепей постоянного тока методом эквивалентного генератора. Расчёт электрических цепей постоянного тока методом суперпозиции(наложения) Параметры синусоидального тока и его представление комплексными величинами. Пассивные элементы в цепях синусоидального тока. Законы Ома и Кирхгофа для цепей синусоидального тока. Пассивные дифференцирующие цепи. Простейшая дифференцирующая RC – цепь аналогична интегрирующей RC – цепи и отличается только тем, что выходное напряжение снимается не с конденсатора, а с активного сопротивления R(рис.1).
Рассмотрим реакцию цепи на прямоугольный импульс длительностью С момента окончания входного импульса в цепи действует только напряжение ис, которое через генератор импульсов (его внутреннее сопротивление считаем равным нулю) прикладывается к выходу, т. е. RC-цепь с постоянной времени, много меньшей длительности входного импульса, называют дифференцирующей. Ток через конденсатор связан с напряжением на нем дифференциальной зависимостью
Расчёт параллельной RC-цепи. вопрос 10 Комплексное сопротивление и комплексная проводимость. Отношение комплексной амплитуды напряжения на зажимах двухполюсника к комплексной амплитуде тока, протекающего через эти зажимы, называется комплексным сопротивлением пассивного двухполюсника
Модуль комплексного сопротивления, равный отношению амплитуды напряжения к амплитуде тока называется полным сопротивлением двухполюсника, т.е. z=mod(Z)= Um/ Im,Ом. Аргументом комплексного сопротивления является фазовый сдвиг между напряжением и током на зажимах двуполюсника, т.е. j = yu -yi. Представляя комплексное сопротивление, как комплексное число, в алгебраической форме, получим Z=z Cosj +j z Sinj = Вещественная и мнимая части комплексного сопротивления двухполюсника носят название соответственно активной и реактивной составляющих комплексного сопротивления. Величина обратная комплексному сопротивлению называется комплексной проводимостью Модуль комплексной проводимости, равный отношению амплитуды тока к амплитуде напряжения называется полной проводимостью двухполюсника, т.е. y=mod(Y)= Im/ Um,Сим. Аргументом комплексной проводимости является фазовый сдвиг между напряжением и током на зажимах двуполюсника, взятый со знаком (-) Представляя комплексную проводимость, как комплексное число, в алгебраической форме, получим Y=y Cosj -j y Sinj = Вещественная и мнимая части комплексной проводимости двухполюсника носят название соответственно активной и реактивной составляющих комплексной проводимости.
Добротность цепи. Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. Общая формула для добротности любой колебательной системы: где: f — частота колебаний W — энергия, запасённая в колебательной системе Pd — рассеиваемая мощность. Для последовательного Колебательного контура в RLC цепях, в котором все три элемента включены последовательно: Q= где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно. Для параллельного контура, в котором индуктивность, емкость и сопротивление включены параллельно: Q=R
Законы коммутации. Закон коммутации на индуктивности Закон коммутации на индуктивности можно сформулировать так: при коммутации ток индуктивного элемента (рис 1.2) не может изменяться скачком.
Закон коммутации можно записать следующим образом: Покажем, что при коммутации ток индуктивного элемента не может изменяться скачком на, основе закона сохранения энергии.
Учитывая, что в момент (0-): в момент 0+: За несуществующий промежуток времени энергия не может измениться, тогда отсюда следует: Закон коммутации на емкости Рассмотрим закон коммутации на емкости по аналогии с законом коммутации на индуктивности. Напряжение на емкости при корректной коммутации не может изменяться скачком:
Заряд конденсатора зависит от напряжения: q = CU В случае некорректной коммутации (рис. 1.5) должны быть равны суммарные заряды конденсаторов: Пусть
В этом случае так же, как и при коммутации на емкости, при замыкании ключа возникает дуга, которая будет гореть до тех пор, пока напряжения на конденсаторах не сравняются. Суммарные заряды равны:
отсюда, напряжение в первый момент после коммутации равно:
Потери в магнитопроводе. Классификация потерь. При работе электрической машины в ее активных материалах возникают потери энергии. К ним относятся магнитные потери в стали магнитопровода и электрические потери в проводниках обмоток. При вращении машины возникают механические потери, вызываемые трением. Кроме того, имеют место добавочные потери в обмотках и в стали магнитопровода. Магнитные потери. Явление электромагнитной индукции связано с изменением магнитного потока, вследствие чего на участках магнитопровода возникают потери на перемагничивание и вихревые токи. Потери на перемагничивание зависят от характера перемагничивания, которое может быть вращательным (возникающим при вращении стального магнитопровода в магнитном поле), циклическим (производимое переменным током) и статическим (при медленном изменении намагничивающего тока в определенных пределах). Потери на вихревые токи в листах стали зависят от свойств материала и толщины листов. Для снижения этих потерь уменьшают толщину листов и изолируют их друг от друга. При расчете потери на перемагничивание и вихревые токи обычно не разделяют. Потери в стали рассчитывают отдельно для каждого участка магнитопровода, имеющего одинаковую магнитную индукцию. Определив значение магнитной индукции, находим удельные потери на 1 кг массы pc = p0 (
Где po – удельные магнитные потери (при индукции В=1,0 тл и частоте f = 50 гц), значение которых зависит от сорта стали и толщины листа (po = 1,2 / 4 вт/кг); f – частота перемагничивания, гц; В – индукция на участке магнитопровода, тл. Общие потери в стали pc = Здесь pci – удельные потери i-го участка магнитопровода; Gi – вес i-го участка магнитопровода. Электрические потери. При прохождении тока по проводникам возникают потери энергии. В машинах имеют место следующие виды электрических потерь: 1) потери в проводниках обмотки якоря Pa = m где Ia – действующее значение тока в обмотке, a; ra – активное сопротивление обмотки якоря, определенное с учетом нагрева, ом; m – число фаз (для машин постоянного тока следует принять m=1); 2) потери в отмотке возбуждения Pn = Где IB – ток обмотки возбуждения, a; rB – сопротивление обмотки возбуждения, определяемое с учетом нагрева, ом; 3) потери в щеточных контактах Pщ = 2 ΔUщIщ; Где ΔUщ – падение напряжения в щелочном контакте Iщ – ток в щетках, a. Общие электрические потери равны сумме Активное сопротивление обмоток микромашин является относительно большим, поэтому электрические потери в микромашинах имеют относительно большую величину, чем в других электрических машинах.
Законы Ома и Кирхгофа для цепей постоянного тока. Разветвленными называются цепи, содержащие узлы, т. е. точки, к которым подходит не менее трех проводников. Поскольку энергия в узлах накапливаться не может, сумма токов, притекающих в любой момент к узлу, равна сумме токов, утекающих от узла. Данное правило называется первым законом Кирхгофа. Закон, устанавливающий равенство между алгебраической суммой мгновенных значений ЭДС в замкнутом контуре и алгебраической суммой мгновенных падений напряжений на всех элементах этого же контура, называется вторым законом Кирхгофа.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.27.153 (0.008 с.) |


 (рис. 2), когда
(рис. 2), когда 
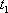 появления импульса положительный скачок напряжения Um выделяется на выходе, затем начинается зарядка конденсатора и напряжение на выходе становится практически равным нулю задолго до окончания входного импульса.
появления импульса положительный скачок напряжения Um выделяется на выходе, затем начинается зарядка конденсатора и напряжение на выходе становится практически равным нулю задолго до окончания входного импульса. с точностью до знака повторяет напряжение ис. Поэтому в момент
с точностью до знака повторяет напряжение ис. Поэтому в момент  на выходе цепи появляется напряжение Umс отрицательной полярностью на верхнем (по схеме рис. 1) и с положительной на нижнем концах резистора R.. Этот отрицательный перепад быстро спадает до нуля, так как конден сатор быстро разряжается.
на выходе цепи появляется напряжение Umс отрицательной полярностью на верхнем (по схеме рис. 1) и с положительной на нижнем концах резистора R.. Этот отрицательный перепад быстро спадает до нуля, так как конден сатор быстро разряжается.

 (Ом)
(Ом)
 , Ом.
, Ом.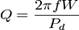


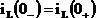
 и
и 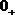 – одна и та же величина по определению закона сохранения энергии, запишем выражения энергии:
– одна и та же величина по определению закона сохранения энергии, запишем выражения энергии:

 ,
,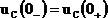
 , а
, а  (либо
(либо  )
)


 ) 1.3 B2,
) 1.3 B2,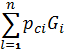 ;
;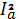 ra;
ra; rB;
rB;


