
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мощность в цепях синусоидального токаСодержание книги Поиск на нашем сайте Активная – энерги, кот выдел в ед врем в виде теплоты на уч цепи в сопрот R P=UIcos(a)=I2r Реактивная- эн, кот отдается ист питания на созд перемн индукт и емкости Q=UIsin(a)= I2X ПолнаяS=UI S2 =P 2 +Q 2
S=P+jQ
Мгновенное значение мощности.
Здесь обозначили и назвали: U×I=S – полная мощность, ВА; U×I×Cos j=P – активная мощность, Вт; U×I×Sin j=Q – реактивная мощность, ВАР.
Передача максимума мощности от источника в нагрузку Условие передачи максимальной мощности от источника к приёмнику.
Первое условие:
Тогда получим:
Получили второе условие:
Максимальная мощность, которая выделится на нагрузке:
Для передачи макс мощности от ист в нагр акт сопр ист и нагр равны между собой
Комплексный(символический) метод расчета, переход от вещественных функций к комплексным
Закон Ома и Кирхгофа в комплексном виде Комплексное сопротивление Закон Ома
Закон Кирхгофа 1-й алгебр сумма мгнов знач токов,сход в любом узле =0: 2-й 22. Расчет цепей символическим методом: метод преобразований, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора Поскольку первый и второй законы Кирхгофа справедливы и для цепей синусоидального тока, можно было бы записать уравнения для мгновенных значений величин цепей синусоидального тока, перейти от них к уравнениям в комплексах и затем повторить вывод всех формул для цепей синусоидального тока. Понятно, что проделывать выводы заново нет необходимости. В том случае, когда отдельные ветви электрической цепи синусоидального тока не связаны между собой магн, все расчетные формулы пригодны и для расчета цепей синусоидального тока, если в этих формулах вместо постоянного тока I подставить комплекс тока, вместо проводимости g — комплексную проводимость У, вместо сопротивления R — комплексное сопротивление Z и вместо постоянной ЭДС Е — комплексную ЭДС Ё.
Графоаналитический метод расчета. Векторные диаграммы Графоаналитический метод расчёта – это совок графического метода и метода пропорц пересчёта. Метод основан на линейной зависимости между токами и напряжениями. Поэтому векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения, питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения. На диаграмме изменятся лишь масштабы напряжений и токов Для ориентировочных расчетов напряжений и токов применяется также графоаналитический метод расчета. Этот метод методологически связан с методом пропорционального пересчета, однако не использует алгебры комплексных чисел. Пусть, как и в предыдущем методе,
Комплексная мощность источника находится из
где
Индуктивно связанные электрические цепи: ЭДС взаимной индукции, согласное и встречное включение двух катушек индуктивности 1. Последовательное соединение индуктивно связанных катушек при согласном включении.
Переходя к синусоидальному току 2. Последовательное соединение индуктивно связанных катушек при встречном включении.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.62 (0.007 с.) |



 , BA
, BA ; то же для Zn
; то же для Zn 














 или
или 

 Выбрав масштабы
Выбрав масштабы  и
и  для напряжений и токов, откладывают в произвольном направлении ток
для напряжений и токов, откладывают в произвольном направлении ток  (например горизонтально). Затем строят вектор напряжения
(например горизонтально). Затем строят вектор напряжения  совпадающий по направлению с током
совпадающий по направлению с током  ,и вектор напряжения
,и вектор напряжения  отстающий по фазе от
отстающий по фазе от  Вычислив
Вычислив  и откладывая ток
и откладывая ток 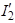 параллельно
параллельно  графически определяют
графически определяют  и т.д. В результате находят вектор условного напряжения U. Затем с помощью коэффициента пересчета K=U/U' вычисляют истинные токи и напряжения. Графические построения по ходу расчета дают в итоге условную топографическую диаграмму. Для получения истинной диаграммы следует, во-первых, увеличить линейные размеры всех векторов в К раз, во-вторых, повернуть против часовой стрелки условную диаграмму на угол
и т.д. В результате находят вектор условного напряжения U. Затем с помощью коэффициента пересчета K=U/U' вычисляют истинные токи и напряжения. Графические построения по ходу расчета дают в итоге условную топографическую диаграмму. Для получения истинной диаграммы следует, во-первых, увеличить линейные размеры всех векторов в К раз, во-вторых, повернуть против часовой стрелки условную диаграмму на угол  , равный разности начальных фаз векторов
, равный разности начальных фаз векторов  и.
и.  Активная и реактивная мощности потребителей вычисляются по формулам
Активная и реактивная мощности потребителей вычисляются по формулам

 – комплексное напряжение источника;
– комплексное напряжение источника; – сопряженный комплексный ток источника.
– сопряженный комплексный ток источника.

 то же для 1
то же для 1






 то же для 2
то же для 2





