
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет электрических цепей методом пропорционального пересчетаСодержание книги
Поиск на нашем сайте
Для расчета цепи на рис.3.2, а также более сложных цепей лестничной структуры применяется метод пропорционального пересчета (МПП). В этом методе используется свойство линейной зависимости всех токов и напряжений цепи от амплитуды напряжения (тока) источника (в цепи единственный источник). Поясним суть метода для цепи на рис.3.2. Задается условно значение тока в наиболее удаленной и сложной ветви цепи. Пусть, например, Тогда
Разделив истинное напряжение
Для получения истинных напряжений и токов цепи необходимо все найденные ранее условные напряжения и токи умножить на коэффициент К, т.е.
Потенциальная диаграмма и ее построение Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
Потенциальная диаграмма построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал ja принят равным нулю. Точка цепи, потенциал которой условно принимается равным нулю, называется базисной. Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса.
Энергетический баланс в электрических цепях При протекании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС Е, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени (мощность), равную ЕI, и произведение ЕI входит в уравнение энергетического баланса с положительным знаком. Если же направление тока I встречно направлению ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение Е1 войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид Когда схема питается не только от источников ЭДС, но и от источников тока,
Синусоидальный ток в активном сопротивление, индуктивности и емкости. а) Синусоидальный ток в активном сопротивлении
б) Синусоидальный ток в индуктивности
Видно, что активная мощность pL=0, a QL= U×I = I2×XL в) Синусоидальный ток в ёмкости
Как и на индук, на емкости акт мощн PС=0, а реактивная QС= U×I = I2×XС
Синусоидальный ток в последовательно включённых RLC
Допустим, что
где величину XL–XC=X назвали реактивным сопротивлением.
Разделив все напряжения на ток, можно получить треугольник сопротивлений.
Синусоидальный ток в параллельно включенных RLC
где
Если изобразить расчет тока в цепи в виде векторов, то получи:
Разделив токи на напряжения, получим треугольник проводимостей.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.86 (0.005 с.) |

 . Затем, находя условное напряжение
. Затем, находя условное напряжение  и условный ток
и условный ток  сложив токи
сложив токи  , находят ток
, находят ток  .
.
 на условное
на условное  вычисляют комплексный коэффициент пересчета К:
вычисляют комплексный коэффициент пересчета К:







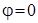



 P=
P= 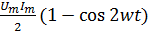


 , ток в катушке отстаёт от приложенного к ней напр на
, ток в катушке отстаёт от приложенного к ней напр на  ;
; а величину XL=
а величину XL=  ×L называют индукт сопрот, индукт провод
×L называют индукт сопрот, индукт провод  .
. .
. ,
,  - ток в конденсаторе опережает приложенное к нему напряжения на
- ток в конденсаторе опережает приложенное к нему напряжения на 
 – емкостное сопротивление, размерность – Ом.
– емкостное сопротивление, размерность – Ом.



 , т.е.
, т.е. 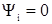 . Тогда по второму закону Кирхгофа:
. Тогда по второму закону Кирхгофа: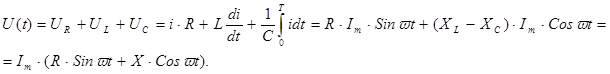
 ;
;  , где
, где  ,полное сопр
,полное сопр

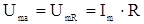

 – цепь имеет индуктивный характер.
– цепь имеет индуктивный характер.

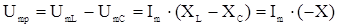
 – цепь имеет емкостной характер.
– цепь имеет емкостной характер.
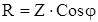 ;
;  .
. Допустим
Допустим  ,
,  .По 1-му закону Кирхгофа:
.По 1-му закону Кирхгофа:
 – активная проводимость;
– активная проводимость;  – индуктивная;
– индуктивная; 
 – реактивная проводимость.
– реактивная проводимость.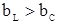






 ;
; 



