
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема наложения и метод расчета эл цепейСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Метод наложения основан на применении принципа наложения, который формулируется следующим образом: Ток в любой ветви электрической цепи равен сумме токов, обусловленных действием каждого источника в отдельности, при отсутствии других источников. При действии только одного из источников напряжения предполагается, что э.д.с. всех остальных источников равны нулю, так же как равны нулю и токи всех источников тока. Отсутствие напряжения на зажимах источников напряжения равносильно короткому замыканию их зажимов. Отсутствие тока в ветви с источником тока равносильно разрыву этой ветви. Если источник э.д.с. содержит внутреннее сопротивление, то, полагая э.д.с. равной нулю, следует оставлять в его ветви внутреннее сопротивление. Аналогично в случае источника тока с параллельной внутренней проводимостью, следует, разрывая ветвь источника (т.е. полагая J=0), оставлять включенной параллельную ветвь с внутренним сопротивлением. Пусть в цепи действуют источники с параметрами E и J, I//n и I/n – токи n-ой ветви, создаваемые каждым из этих источников в отдельности. Искомый ток
Теорема компенсации В электрической цепи любой пассивный элемент можно заменить эквивалентным источником напряжения, э.д.с. которого равна падению напряжения на данном элементе E=U=IR и направлена навстречу ему. Справедливость этого утверждения вытекает из того, что любое из слагающих падения напряжений, входящих в уравнения по второму закону Кирхгофа может быть перенесено в другую сторону уравнения с противоположным знаком, т.е. может рассматриваться как дополнительная э.д.с., направленная навстречу току.
Рис. 31. Иллюстрация к теореме компенсации.
Если в ветвь ''ab'' рис.31,а последовательно включить две равные, но противоположно направленные э.д.с. E/=E//=IR, то точки ''a'' и ''d'', ''c'' и ''b'' оказываются соответственно точками одинакового потенциала:
Таким образом, закоротив точки ''a'' и ''d'' и исключив, получим этот участок из ветви «ab», получим схему рис. 31,в. Ток ветви при этом не изменится.
Теоремы об экв ист ЭДС и тока и расчет цепей на их основе. Теорема об эквивалентном источнике напряжения. По отношению к зажимам произвольно выбранной ветви оставшаяся активная часть цепи (активный двухполюсник) может быть заменена эквивалентным генератором. Параметры генератора: его э.д.с. Eэкв. Равна напряжению на зажимах выделенной ветви при условии, что эта ветвь разомкнута, т.е. Eэкв.=Uxx; его внутренне сопротивление r0 равно эквивалентному сопротивлению пассивной электрической цепи со стороны зажимов выделенной ветви.
Данная теорема доказывается следующим образом: в ветвь ab две одинаковые по величине и противоположно направленные э.д.с. E1=E2 при условии, что они равны напряжению холостого хода между зажимами a-b: E1=E2=Uxx. В соответствии с принципом наложения определяем ток Ik как сумму двух токов: Ik, возникающего под действием э.д.с. E1 и всех источников оставшейся части схемы, и тока Ik//, возникающего от независимого действия источника E2. Ток Ik/=0, т.к. E1=Uxx Ток Ik/=Ik в эквивалентной схеме, называемой схемой Гемгольца-Тевенина равен
Теорема об эквивалентном источнике тока. Ток в любой ветви «a-b» линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока. Ток этого источника должен быть равен току между зажимами a-b закороченными накоротко, а внутренняя проводимость источника тока должна равняться входной проводимости пассивной электрической цепи со стороны зажимов «a» и «b» при разомкнутой ветви «ab».
Действительно, из условия эквивалентности источников тока и напряжения следует: источник напряжения э.д.с. которого равна Uxx, а внутренне сопротивление равно r0 может быть заменен источником тока:
Jэкв., определенное по формуле (43), является током короткого замыкания, т.е. током, проходящим между зажимами «a-b», замкнутыми накоротко. Искомый ток ветви «k» равен:
где
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.23.93 (0.008 с.) |





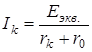

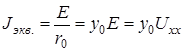
 (44)
(44)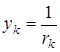 .
.


