Семантика ИВ. Теоремы полноты и адекватности.

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Метатеоремы – это теоремы о самой теории, в нашем случае АВ и ИВ.

1) Метатеоремы АВ.

а) АВ не противоречива, в том смысле, что, никакое высказывание не может быть одновременно истинным и одновременно ложным, более того, никакая формула не может быть одновременно тавтологией и опровержимой.

б) АВ полна, в том смысле, что о каждой формуле можно судить, является ли она тавтологией или нет.

в) Более того, существует механизм определения характера формулы (таблицы истинности). В этом смысле АВ называют еще разрешимой теорией.

2) АВ является важнейшей содержательной интерпретацией ИВ (говорят, что АВ выступает в качестве семантики ИВ).

3) Об этом говорят следующие теоремы полноты и адекватности.

Теорема полноты. Формула F выводима в ИВ тогда и только тогда, когда F – тавтология в АВ.

Теорема легко доказывается в части необходимости. Так, если F выводима в ИВ, то F:

а) Может быть аксиомой, но каждая формула-аксиома рассматриваемая в АВ, как легко проверить, есть тавтология (при этом не важно будут ли переменные, содержащиеся в этой формуле пропозиционными или некоторые из них суть обозначений формул).

б) Формула F получена из двух предыдущих на основе ПЗ.

├H; ├(H→F), значит, ├F. В этом случае, при условии, что Н – выводима и тавтология в АВ, а также при условии, что (H→F) тавтология в АВ, будет действовать то же ПЗ в АВ и, значит, F там тавтология.

Теперь остается к H и (H→F) применить подходящее из рассуждений а) и б), так что окончательно F будет тавтологией.

На основе правила выводимости других ситуаций относительно F быть не может.

Теорема адекватности. Если формула F выводима из последовательности F├{B₁, B₂, …, B_n} в ИВ, то F есть логическое следствие из группы формул {B₁, B₂, …, B_n} в АВ.

Обратно. Формула в АВ является логическим следствием групп формул, выводимых из них же в ИВ.

Говоря о выводимости, мы ограничиваемся конечным количеством гипотез, что логично сделать, как доказано выше.

Достаточность. Дано, что в АВ (B₁, B₂, …, B_n)├F. Применим следствие теоремы дедукции а АВ. На его основе мы имеем тавтологию B₁→(B₂→…→(B_n→F)…))). На основе теоремы полноты, написанная тавтология обязаны быть выводима в ИВ.

Теперь применим в ИВ теорему, обратную теореме дедукции и получаем, что (B₁, B₂, …, B_n)├F в ИВ.

Точно так же доказывается обратное утверждение с переходом на основании теоремы полноты из АВ в ИВ.

2) Метатеоремы относительно ИВ.

а) ИВ не противоречиво. Это означает, что любая формула в ИВ не может быть одновременно выводимой и не выводимой. Иначе бы на основании теоремы полноты оказалась бы противоречива АВ.

б) ИВ – полная теория, в том смысле, что относительно каждой формулы в ИВ можно сказать выводима она или нет. Действительно, на основании теоремы полноты вопрос сводится к выяснению характера формулы в АВ, но АВ – полная теория.

в) ИВ – разрешимая теория. Это означает, что существует алгоритм проверки выводимости каждой формулы в ИВ.

Алгоритм состоит в следующем:

1. Рассмотреть эту же формулу в АВ.

2. Составить для нее таблицу истинности.

3. Установить характер ее а АВ.

4. Применить теорему полноты.

Алфавитный оператор.

1) Алфавит G – конечное множество символов произвольной природы, а слово g – упорядоченное множество (конечная последовательность символов алфавита, при этом символы в слове могут повторяться).

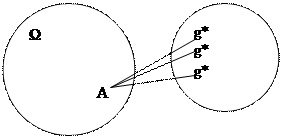
2) Пусть даны два алфавита G и G*. Алфавитным оператором А, определенным на множестве Ω слов алфавита G, называется соответствие, которое каждому символу gєΩ сопоставляет одно или несколько слов в алфавите G*. Слово g* (слова g*) называют образами слова g. Множество Ω называется областью определения алфавитного оператора А, а множество всевозможных получаемых в результате действия оператора А образов Ω* называется областью значений оператора А.

В этом определении оператор А может быть как однозначным, так и многозначным.

3) Если оператор А однозначный и различным прообразом g соответствуют различные g*, то существует однозначный обратный оператор

_А

А^-1:g* ׀→ g. Его область определения служит Ω*, а множество значений будет Ω.

4) К понятию алфавитного оператора тем или иным способом можно свести практически любые способы преобразования информации, а значит, об алгоритмах можно теперь говорить как о способах задания алфавитных операторов. Слова исходного алфавита G часто называют входными, а их образы – выходными словами.

Часто рассматривают случай G≡G*. Тогда говорят, что оператор А действует в алфавите G. Поскольку алфавитный оператор есть очень общее понятие, включающее в себя очень многие объекты (например, функции в математике), то и способы его задания, т.е. способы преобразования входных в выходные могут быть самыми разными. Важно только, чтобы за конечное количество шагов каждое входное слово было преобразовано в выходное (выходные).

Такими способами могут быть:

а) В случае конечного набора Ω и конечно-значного оператора таблица

Входное слово

Выходное слово

б) Посимвольное отображение, т.е. задан способ по которому каждый символ αєG соответствовал единственный символ βєG*. В этом случае каждому слову gєΩ соответствует единственное слово g*єΩ*, которое состоит из каждого символа, входящего в g.

в) Кодирующее отображение. Здесь каждому символу αєG соответствует конечная последовательность символов алфавита G* - так называемый код.

α |→β₁, β₂, …, β_k.

В этом случае набор кодов определяет для каждого gєΩ соответствующее слово g*єΩ*.

г) Другие способы.

⇐ Предыдущая 1 2 3 4 5 6 789 10 Следующая ⇒

Последнее изменение этой страницы: 2016-04-19; Нарушение авторского права страницы

infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.80.218.53 (0.006 с.)