
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о вероятности суммы событийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теорема о вероятности суммы событий Теорема сложения вероятностей Суммой двух случайных событий А и В называется события А + В состоящие в наступление хотя бы одного из событий А или В. А А + В: 1) только А или 2) только В Теорема сложения для 2-х несовместных событий Если А и В – несовместны, то вероятность наступления только одного из двух несовместных событий равна сумме вероятностей этих событий Р(А+В) = Р(А)+Р(В) Следствие: эта теорема применима для любого конечного числа несовместных событий Р(А+В+С) = Р(А)+Р(В)+Р(С) Теорема сложения для полно группы событий Пусть события В₁, В₂,… Теорема сложения для противоположных событий Р(Ā)+Р(А)=1. Сумма вероятностей противоположных событий равна 1. Условные вероятности. Теорема о вероятности произведения событий Теорема умножения вероятностей Пусть любое случайное событие называется событие А и В, состоящие в совместном наступление событий А и В Случайное событие (с.с.) – то, что может произойти или не произойти при осуществление определенной совокупности условий S Если никаких других ограничений кроме условия S на случайное событие не накладывается, то вероятность этого события называется безусловной и обозначается Р(А) Условной вероятностью события В называется вероятность этого события, вычисленную в предположении, что событие А уже произошло и обозначается Событие Теорема Пусть А и В – зависимое с.с. Р(А*В) = Р(А)* Вероятность совместного наступления двух зависимых событий равна произведению вероятности одного, на условную вероятность другого, вычисленную предположением, что первое событие уже произошло Теорема Пусть А и В – независимое с.с.
Так как вероятность события В не изменяется в зависимости от того, происходит событие А или нет Теорема Пусть А и В – независимое с.с. Р(А*В) = Р(А)*Р(В) Вероятность совместного наступления всех независимых событий равна произведению вероятностей этих событий Теорема Пусть А,В,С…К, L – зависимое с.с Р(А,В,С…К, L) = Р(А)* Вероятность совместного наступления конечного числа зависимых событий равна произведению условных вероятностей этих событий относительных произведению предшествующих каждому из них Теорема Пусть А,В,С…К, L – независимое с.с. Р(А,В,С…К, L) = Р(А)*Р(В)*Р(С)…*Р(L) Вероятность наступления конечного числа независимых событий равна произведению вероятностей этих событий Формула полной вероятности Пусть событие А может произойти лишь при условии наступления одного из независимых событий В₁, В₂,.. Теорема Р(А) = Р(В₁)* Вероятность события А, которое может произойти лишь при условии наступления одного из независимых событий В₁, В₂,.. Формула Байеса Р(А) – вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂,.. В связи с тем, что не известно, которое из событий В₁, В₂,..
Найдем вероятность совместного наступления событий А и В₁. Используем теорему умножения для 2-х зависимых событий Р(А*В₁) = Р(А)* Р(В₁*А) = Р(В₁)* Т.к. в левой части обоих формул находятся вероятность одного и того же события, левые части равны, равны и правые Р(А)* Аналогично можно получить формулы для условных вероятностей остальных гипотез
Эти формулы называются формулой Байеса в которых вероятность А в значении находится по формуле полной вероятности: Р(А) = Р(В₁)* Формула Бернулли
В общем случае можно утверждать, что вероятность наступления события А в n независимых испытаниях: 1) не менее К раз:
2) не более К раз
3) более К раз
4) менее К раз
Случайные величины Переменные величины которые принимают различные значения в зависимости о случая, называются случайные величины Обозначаются: заглавными латинским буквами X;Y;Z.. значение, которое принимают случайные величины в результате испытания, называют ее возможные значения Х – число очков, выпавших при подбрасывание игральной кости: х₁=1, х₂=2,х₃=3,х₄=4,х₅=5,х₆=6 Случайные величины подразделяются на 2 вида: дискретные и непрерывные Дискретной называют случайную величину, возможное значение которой образует дискретный ряд чисел. Число этих значений может быть конечным и бесконечным. Непрерывной называют случайную величину, возможное значение которой полностью заполняет некоторый промежуток (конечный или бесконечный). Число всегда бесконечно Нормальное распределение. Нормальный закон распр-я н.с.в. – закон, который хар-ся след.пл-тью распр-я.
Q= D(Х) под корнем = Q (Х), → параметр a = мат. ожид-ю, а пар. Q = среднему квадратич. О откл- ю нормально распр-ой с.в.х. Вариационный ряд. Вариационный ряд - последовательность всех элементов выборки, расположенных в неубывающем порядке. Одинаковые элементы повторяются. По этому ряду уже можно сделать несколько выводов. Например, средний элемент вариационного ряда (медиана) может быть оценкой наиболее вероятного результата измерения. Первый и последний элемент вариационного ряда (т.е. минимальный и максимальный элемент выборки) показывают разброс элементов выборки. Иногда если первый или последний элемент сильно отличаются от остальных элементов выборки, то их исключают из результатов измерений, считая, что эти значения получены в результате какого-то грубого сбоя, например, техники. 17. Графическое изображение вариационных рядов, полигон и гистограмма. Графическое изображение вариац. рядов: 1. Полигонная частота- линия отрезка, которой соединяют точки с координатами (х1,н1) (х2,н2) (хн,нк). Точки соединяются с координатами (х1,в1) (х2,в2) (хн,вн). 2. Для непрерывного распр-я колличеств-ти признака Х, используют гистограмму частот или относит. частот. Для гистограммы относит. частот высоты прямоугол = ви: альфа. Теорема о вероятности суммы событий Теорема сложения вероятностей Суммой двух случайных событий А и В называется события А + В состоящие в наступление хотя бы одного из событий А или В. А А + В: 1) только А или 2) только В Теорема сложения для 2-х несовместных событий Если А и В – несовместны, то вероятность наступления только одного из двух несовместных событий равна сумме вероятностей этих событий Р(А+В) = Р(А)+Р(В) Следствие: эта теорема применима для любого конечного числа несовместных событий Р(А+В+С) = Р(А)+Р(В)+Р(С) Теорема сложения для полно группы событий Пусть события В₁, В₂,… Теорема сложения для противоположных событий Р(Ā)+Р(А)=1. Сумма вероятностей противоположных событий равна 1.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1451; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.152 (0.007 с.) |

 В: 1) только А или 2) только В или 3) А и В
В: 1) только А или 2) только В или 3) А и В образуют полную группу. Сумма вероятностей событий, образующих полную группу равна 1. Р(В₁)+Р(В₂)+…+Р(
образуют полную группу. Сумма вероятностей событий, образующих полную группу равна 1. Р(В₁)+Р(В₂)+…+Р(
 называется зависимым о события А, если вероятность события В изменяется в зависимости от того, происходит ли событие А или нет. Если не изменяется, то событие А и В – независимы
называется зависимым о события А, если вероятность события В изменяется в зависимости от того, происходит ли событие А или нет. Если не изменяется, то событие А и В – независимы

 )*
)*  А)+…+Р(
А)+…+Р( *
*  – формула полной вероятности
– формула полной вероятности


 = Р(В₁)*
= Р(В₁)* 


 +…+ Р(
+…+ Р(
 – вероятность того, что в n независимых испытаниях событие А произойдет равно К раз
– вероятность того, что в n независимых испытаниях событие А произойдет равно К раз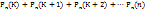



 → норм-ый закон опред-ся двумя параметрами а и (жигма)
→ норм-ый закон опред-ся двумя параметрами а и (жигма)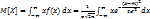 = а
= а = Q₂
= Q₂


