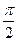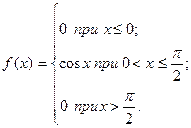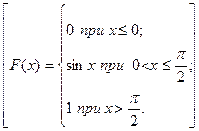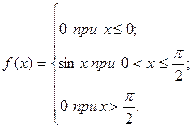Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события и вероятностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ГЛАВА I СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТИ Случайные события. Классическое определение вероятности 1. Понятие о случайном событии. Опыт, эксперимент, наблюдение явления называют испытанием. Испытаниями, например, являются: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенным на каждую грань числом очков — от одного до шести). Результат, исход испытания называется событием. Событиями являются: выпадение герба или цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д. Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании. Пример1. Испытание: однократное бросание игральной кости. Событие А — появление четырех очков, событие В — появление четного числа очков. События А и В совместимые. Определение 2. Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании. Пример 2. Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В— выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого. Несовместимость более чем двух событий в данном испытании означает их попарную несовместимость. Пример 3. Испытание: однократное бросание игральной кости. Пусть события А1, Аг, А3, А Определение 3. Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит. Событие, противоположное событию А, обозначают через П р и м е р 4. Испытание: однократное бросание монеты. Событие А — выпадение герба, событие В— выпадение цифры. Эти события противоположны, так как исходами бросания могут быть лишь они_и появление одного из них исключает появление другого, т. е. А = Определение 4. Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти. Пример 5. Испытание: извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие. Заметим, что достоверное и невозможное события в данном испытании являются противоположными. Определение 5. Событие А называется случайным, если оно объективно может наступить или не наступить в данном испытании. Пример 6. Событие А6 — выпадение шести очков при бросании игральной кости — случайное. Оно может наступить, но может и не наступить в данном испытании. Пример 7. Событие А98 — прорастание девяноста восьми зерен пшеницы из ста — случайное. Это событие может наступить, но, может быть, прорастет зерен больше или меньше. Алгебра событий. Определение 1. Суммой событий A и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В. Пример 1. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадание в мишень первым стрелком, событие В — попадание в мишень вторым стрелком. Суммой событий А и В будет событие С=А+В, состоящее в попадании в мишень по крайней мере одним стрелком. Аналогично суммой конечного числа событий А Из определения 1 непосредственно следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А+А=А (а не 2А, как в алгебре). Определение 2. Произведением событий А и В называется событие С=АВ, состоящее в том, что в результате испытания произошли и событие А, и событие В. Аналогично произведением конечного числа событий А В условиях предыдущего примера произведением событий А и В будет событие С=АВ, состоящее в попадании в мишень двумя стрелками. Из определения 2 непосредственно следует, что АВ = ВА. Справедливы также сочетательный и дистрибутивный законы. Однако АА = А (а не Аг). 3. Классическое определение вероятности. Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания. Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них. Примеры полных групп событий — выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости. Рассмотрим полную группу попарно несовместимых событий U1,U2,..., Un,, связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий U Определение 2. События U Пример 1. Вернемся к опыту с подбрасыванием игральной кости. Пусть U Определение 3. Событие А называется благоприятствующим событию В, если наступление события А влечет за собой наступление события В. Пример 2. Пусть при бросании игральной кости события U2, U4 и U 6 — появление соответственно двух, четырех и шести очков, а А — событие, состоящее в появлении четного числа очков; события U2, U4 и U 6 благоприятствуют событию А. Определение 4 (классическое определение вероятности). Вероятностью Р(А) события А называется отношение т/п числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Р(А) = т/п. Пример 3. Вычислим вероятность выпадения герба при одном бросании монеты. Очевидно, событие А — выпадение герба — и событие В— выпадение цифры — образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь п = 2. Событию А благоприятствует лишь одно событие—само А, т.е. здесь m=1. Поэтому Р(А) = П р и м ер 4. Очевидно, что при одном бросании игральной кости (вероятность выпадения какой-либо цифры от 1 до 6 будет равна P(U Пример 5. Найдем вероятность того, что при однократном бросании игральной кости выпадет число очков, делящееся на 2 (событие А). Число элементарных событий здесь 6. Число благоприятствующих элементарных событии 3 (выпадение 2, 4 и 6). Поэтому
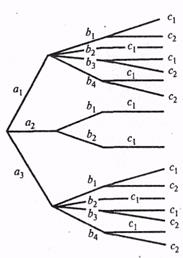
Пример 6. При составлении команды космического корабля возникает вопрос о психологической совместимости отдельных членов экипажа. Допустим, что надо составить команду из трех человек: командира, инженера и врача. На место командира есть три кандидата: а1, а2 , a 3; на место инженера — четыре кандидата: Ь Представим все варианты команды, при которых члены экипажа совместимы друг с другом в виде «дерева» (рис. 1). Число ветвей этого дерева, т. е. исходов, благоприятствующих событию А,равно 16, а общее число возможных комбинаций по правилу произведения равно 4 Задача (Вероятности рождения мальчиков и девочек). Будем предполагать, что случаи рождения мальчика Пусть в семье двое детей. Какова вероятность, что оба ребенка — мальчики? Если известно, что один мальчик, какова вероятность, что оба ребенка — мальчики? На первый вопрос ответить нетрудно. Имеется четыре равно-возможных исхода: ММ, МД, ДМ, ДД (М— мальчик, Д— девочка). Исходы МД и ДМ различны, так как в первом из них сначала родился мальчик, а потом девочка, во втором — наоборот. Из этих четырех исходов только один ММ благоприятствует нашему событию. Отсюда следует, что Р(ММ) = Если дополнительно известно, что один ребенок — мальчик, то событие ДД исключается. Из трех равновозможных событий ММ, МД, ДМ по-прежнему только одно ММ благоприятствует желаемому исходу. Поэтому Р(ММ) = Если известно, что старший ребенок— мальчик, то исключаются исходы ДМ и ДД. В этом случае Р(ММ) = Из приведенного классического определения вероятности вытекают следующие ее свойства: 1. Вероятность достоверного события равна единице. Р(А) = т/п = п/п = 1. 2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. т = 0, откуда Р(А) = т/п = 0/п = 0. 3. Вероятность случайного события есть положительное число, Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0<т<п и, значит, 0< т / п <1. Следовательно, 0<Р(А)<1. Таким образом, вероятность любого события удовлетворяет двойному неравенству 0 Замечание. Из определения вероятности следует, что элементарные события являются равновероятными, т. е. обладают одной и той же вероятностью. Свойства вероятности Формула полной вероятности. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из n попарно несовместимых событий В1 В2,..., Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р(А) = Р(В1)РB1(А)+ Р(В2)РB2(А)+...+Р(Вn)РBn(А) (1.14)
(формула полной вероятности)
События В1 В2,..., Вn будем называть гипотезами. Доказательство. Событие А может наступить лишь при условии наступления одного из событий В1 В2,..., Вn, т. е. А = В1 А + + B2+... + Вn А, причем ввиду несовместимости событий В1 В2,... Вn события В1А, В2А,..., Вn А также несовместимы. Поэтому на основании теорем сложения и умножения вероятностей имеем Р(А)+Р(В1 А)+Р(В2 А)+…+Р(Вn А)=Р(В1)РB1(А)+Р(В2)PB2(A)+…+Р(Вn)РBn(А) П р и м е р 1. Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором — три белые и одна серая, в третьем — две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь? Обозначим В1 — выбор первого ящика, В2 — выбор второго ящика,B3— выбор третьего ящика, А — извлечение белой мыши. Так как все ящики одинаковы, то Р(В1)=Р(В2)=Р(В3)=1/3. Если выбран первый ящик, то РВ1(А)=2/3. Аналогично РВ2(А)=3/4 РВ2(А)=3/4 РВ3(А)=1/3 Наконец, по формуле (1.14) получаем Р(А)=1/3*2/3+1/3*3/4+1/3*1/2=23/36.
Пример 2. В санатории 30% пациентов — мужчины (М) и 70%— женщины (Ж). Болезни сердца среди мужчин встречаются два раза чаще, чем среди женщин. Какова вероятность того, что наугал выбранный пациент сердечник? Обозначив С — начилие заболевания сердца, запишем: Р(М) = 0,3, Р(Ж) = 0,7, Рм(С) = 2/3, Рж(С) =1/3 Подставлям эти числа в формулу полной вероятности (1.14), получим Р(С) = 0,3*2/3 + 0,7 *1/3 = 0,23+0,2 = 0,43.. Задача (смог над городом). На город примерно 100 дней в году дует ветер с севера и 200 дней в году — с запада. Промышленные предприятия, расположенные на севере, производят выброс вредных веществ каждый третий день, а расположенные на западе — последний день каждой недели. Как часто город подвергается воздействию вредных выбросов? Иными словами, какова вероятность того, что в наугад выбранный день город будет накрыт промышленным смогом? Обозначив С — ветер с севера, З — ветер с запада и В — воздействие вредных выбросов на город, можем записать: Р(С)=100/365=20/73=0,27; Р(З)=200/365=40/73=0,55; РС(В)=1/3=0,33; РЗ(В)=1/7=0,14. Отсюда по формуле погной вероятности Р(В)=Р(С)Рс(В)+Р(З)РЗ(В)=20/73*1/3+40/73*1/7=0,09+0,08=0,17 Таким образом, около двух месяцев в году город накрыт смогом. 5. Формулы Байеса. Пусть в условиях рассуждения, относящегося к формуле полной вероятности, осуществлено одно испытание, в результате которого произошло событие А. Спрашивается, как изменились (в связи с тем, что событие А уже произошло) вероятности гипотез, т. е. величины Р(Вk),k = 1, 2,..., n? Найдем условную вероятность PA (Вk) По формуле (1.8) (см. п. 2) имеем Р(АВK) = Р(А)РA(ВK) = Р(ВK)РBK(А). Отсюда, РА(Вк)= Р(Вк) РВк(А)/Р(А) Наконец, используя формулу полной вероятности,находим: РА(Вк)= Р(Вк) РВк(А)/ РВк(А)/ Выражения (1.15) называют формулами Байеса*. П р и м е р. Партия деталей изготовлена тремя рабочими, причем первый рабочий изготовил 25% всех деталей, второй — 35%, третий — 40%. В продукции первого рабочего брак составляет 5%, в продукции второго — 4% и в продукции третьего — 2%. Случайно выбранная для контроля деталь оказалась бракованной. Какова вероятность того, что она изготовлена вторым рабочим? Введем обозначения для событий: А — выбранная для контроля деталь оказалась бракованной; В1, В2, В3 — эта деталь изготовлена соответственно первым, вторым и третьим рабочим. Имеем: Р(В1)=0,25; Р(В2)=0,35; Р(В3)=0,40; РВ1(А)=0,05; РВ2(А)=0,04; РВ3(А)=0,02.
По формуле Байеса находим РА(В2)=0,35*0,04/0.25*0.05+0.35*0.04+0.40*0,02=0,4 Как здесь, так и в ряде других примеров для облегчения вычислений можно использовать калькулятор. ГЛАВА 11 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ § 2.1. Дискретные случайные величины 1. Понятие ”случайные величины”. О п р е дел е н и е 1. Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества всезможных значений. П р и м е р ы. 1) Число очков, выпавших при однократном бросании игральной кости, есть случайная величина, она может принять одно из значений: 1, 2, 3, 4, 5, 6; 2) прирост массы домашнего животного за месяц есть случайная величина, которая может иметь значение из некоторого число- вого промежутка; 3) число родившихся мальчиков среди пяти новорожденных есть случайная величина, которая может принять значения 0, 1, 2, 3, 4, 5; 4) расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина, возможные значения которой принадлежат некоторому промежутку. Случайные величины обычно обозначают прописными буквами Х, У, 2 а их возможные значения — соответствующими строчными буквами х, у,. Например, если случайная величина Х имеет три возможных значения, то они будут обозначены так: х1, х2, х3. О п р е д е л е н и е 2. Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной. Рассмотрим дискретные случайные величины, множество допустимых значений которых конечно случайные величины из примеров 1) и 3) дискретные. О п р е д е л е н и е 3. Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной. Случайные величины из примеров 2) и 4) являются непрерывными. О п р е д е л е н и е 4. Под суммой (произведением) случайных величин Х и У понимают случайную величину 7=Х+ У (7= ХУ), возможные значения которой состоят из сумм (произведений) каждого возможного значения величины X и каждого возможного значения величины Y. 2. Законы распределения дискретных случайных величин. Рассмотрим дискретную случайную величину X с конечным множеством возможных значений. Величина X считается заданной, если перечислены все ее возможные значения, а также вероятности, с которыми величина X может принимать эти значения. Указанный перечень всех ее возможных значений и их вероятностей называется законом распределения дискретной случайной величины. Закон распределения дискретной случайной величины может быть задан с помощью таблицы:
В верхней строке выписываются все возможные значения х 1, х 2,..., х n величины X, в нижней строке выписываются вероятности р1, р2,..., pn значений х1, х2, ..., хn. Читается таблица следующим образом: случайная величина X может принимать значения хi с вероятностями рi (i = 1, 2,..., n). Так как события X = хi ( i = 1, 2,..., n) образуют полную группу несовместимых событий, то р1 + р2 +... + pn =1 П р и м е р. В денежной лотерее раньше разыгрывались: 1 выигрыш в 1000 р., 10 выигрышей по 100 р. и 100 выигрышей по 1 р. при общем числе билетов 10 000. Найдем закон распределения случайного выигрыша X для владельца одного лотерейного билета. Здесь возможные значения для X есть: x1 = 0, х2 = 1, х3 = 100, х4 = 1000. Вероятности их будут: p 2 = 0,01, р 3 = 0,001, р 4 = 0,0001, p 1 = 1 - 0,01 - 0,001 - 0,0001 = 0,9889. Следовательно, закон распределения выигрыша X может быть задан таблицей:
В заключение отметим так называемую «механическую» интерпретацию представленной таблицы. Представим себе, что некоторая масса, равная единице, распределена по оси абсцисс так, что в п отдельных точках х1, х2, ..., х n сосредоточены соответственно массы р 1, р 2, ..., p n. Тогда эта таблица описывает систему материальных точек, размещенных на оси абсцисс.
Случайной величины
1. Понятие математического ожидания. Закон распределения полностью задает дискретную случайную величину. Однако часто встречаются случаи, когда закон распределения случайной величины неизвестен. В таких случаях случайную величину изучают по ее числовым характеристикам. Одной из таких характеристик является математическое ожидание. Пусть некоторая дискретная случайная величина X с конечным числом своих значений задана законом распределения:
О п р е д е л е н и е. Математическим ожиданием М(Х) дискретной случайной величины X называется сумма произведений всех возможных значений величины X на соответствующие вероятности:
М(Х) = x1p1 + х2р2 +... + хnрn П р и м е р. Найдем математическое ожидание выигрыша X в примере из § 2.1 (п. 2). Используя полученную там таблицу, имеем М(Х) = 0 • 0,9889 + 1 • 0,01 + 100 • 0,001 + 1000 • 0,0001 = 0,21 (руб.). Очевидно, М(Х) = 21 коп. есть справедливая стоимость одного лотерейного билета. Т е о р е м а. Математическое ожидание дискретной случайной величины X приближенно равно среднему арифметическому всех ее значений (при достаточно большом числе испытаний). Д о к а з а т е л ь с т в о. Предположим, что произведено п испытаний, в которых дискретная случайная величина X приняла значения x 1,..., хk соответственно т1,..., тk раз, так что т1 +... + т k = п. Тогда среднее арифметическое всех значений, принятых величиной X, выразится равенством
или
Так как коэффициент тi/п является относительной частотой события «величина Х приняла значение хi » (i =1, 2,..., k ), то xср = x1p1* + x2p2* +... + xkpk*. Из статистического определения вероятности следует, что при достаточно большом числе испытаний pi* xср или x ср Таким образом, математическое ожидание случайной величины можно приближенно считать ее средним значением, что и делают на практике. Обратимся теперь к механической интерпретации математического ожидания дискретной случайной величины X. Пусть на оси абсцисс расположены точки с абсциссами х1, х2,..., хn,в которых сосредоточены соответственно массы р1, р2,.., pn, причем р1 + р2 +...+ pn = 1. Тогда математическое ожидание М(Х), определяемое формулой (2.1), есть ни что иное, как абсцисса центра масс данной системы материальных точек. Правило трех сигм. Полагая в выражении (2.27), Но Формула (2.28) означает, что событие, состоящие в осуществлении неравенства В заключении заметим, что нормальное распределения вероятностей имеет в теории вероятностей больше значений. Нормальному закону подчиняется вероятность при стрельбе по цели, его используют в теории погрешностей физических измерений и т.п. Закон больших чисел Неравенство Чебышева. Лемма. Пусть X- случайная величина, принимающая только неотрицательные значения, тогда P(X Доказательство. Для простоты докажем это утверждение для дискретной величины Х, принимающие случайные значения x Где суммирование распространено на все значения больше или равные единице. Но для, x Поэтому P(X Добавим к правой части неравенства (2.30) сумму Коэффициент А найдем, возпользовавшись соотношением (2.17). Так как.
Применяем формулу (2.16), получим функцию распределения F(x): F(x)= Наконец формулы (2.9) и (2.12) с учетом найденного значения функции F(x) дают P(0<X<1)=F(1)-F(0)=0,25. Упражнения 1. Пусть случайная величина X— число очков, выпавших при подбрасывании игральной кости. Найдите закон распределения случайной величины X.
2. В денежной лотерее выпущено 100 билетов. Разыгрываются 1 выигрыш в 500 р. и 10 выигрышей по 10 р. Найдите закон распределения случайного выигрыша X для владельца одного лотерейного билета.
3. Закон распределения случайной величины X задан таблицей:
Найдите математическое ожидание случайной величины X. [2,2] 4. Найдите математическое ожидание выигрыша X в упражнении 2. [6 р.] 5. Найдите математическое ожидание случайной величины X, зная
[3,9] 6. Проводятся 2 выстрела с вероятностями попадания в цель, равными p1 = 0,4; p2 = 0,3. Найдите математическое ожидание общего числа попаданий. [0,7] 7. Найдите математическое ожидание суммы числа очков, которые могут выпасть при одном бросании двух игральных костей. [7] 8. Найдите математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей. [12,25] 9. Независимые случайные величины X и Y заданы следующими за
И
Найдите математическое ожидание случайной величины XY. [32,56] 10. Найдите дисперсию случайной величины X, которая задана следующим законом распределения:
[2,01]
Найдите дисперсию суммы этих величин. [7] 12.Дисперсия случайной величины X равна 5. Найдите дисперсию следующих величин: а)X-1; б) -2Х; в)3X+6. [а) 5; б) 20; в) 45] 13—15. Найдите математическое ожидание и дисперсию случайных величин, заданных различными законами распределения: 13.
14.
15.
16. К случайной величине прибавили постоянную α. Как при этом [а) прибавится α; б) не изменится ] 17. Случайную величину умножили на α. Как при этом изменятся: [а) умножится на α; б) умножится на α2]
18. Случайная величина X принимает только 2 значения: 1 или -1, каждое с вероятностью 0,5. Найдите дисперсию D(Х) и среднее квадратическое отклонение σ(Х). [D(X) = 1; σ(x)=1] 19. Дисперсия случайной величины D(Х) = 6,25. Найдите среднее квадратическое отклонение σ(Х). [2,5] 20.Пусть закон распределения случайной величины X задан таблицей:
Определите математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение σ(Х). [M(X)=11;D(X)=33;σ(X)≈5,75] 21. Дискретная случайная величина X задана законом распределения:
Найдите начальные моменты первого и второго порядков. [ν1=4,6; ν2 = 21,8] 22. Дискретная случайная величина X задана законом распределения, приведенным в предыдущем примере. Найдите центральный момент второго порядка. [μ2 = 0,64] 23.Случайная величина X задана функцией распределения
0 при x≤-1 F(x)=
1 при x>2 Найдите вероятность того, что в результате испытания случайная величина X примет значение, заключенное в интервале (0; 1). [ 24.Случайная величина X задана функцией распределения
0 при x≤2 F(x)= 1 при x>4 Найдите вероятность того, что в результате испытания X примет значение, [0,5] 25. Случайная величина X задана плотностью вероятности
0 при x<0 f(x)= 0 при x>4
Найдите вероятность попадания случайной величины X на отрезок [-2; 3]. [ 26. Плотность вероятности случайной величины X задана выражением
Найдите вероятность того, что величина X попадает на интервал (-1; 1). [0,5] 27. Случайная величина задана плотностью вероятности
f(x)= α cos x при - 0 при x> Найдите коэффициент α. [а = 0,5]
28. Дана дифференциальная функция распределения непрерывной случайной величины X
Найдите интегральную функцию распределения F(x).
29. Дана дифференциальная функция распределения непрерывной случайной величины X
Найдите интегральную функцию распределения F(x).
30. Функция
является плотностью вероятности случайной величины X. Найдите коэффициент А и функцию распределения F(x).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |

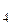 , А5, А 6 — соответственно выпадение одного очка, двух, трех и т.д. Эти события являются несовместимыми.
, А5, А 6 — соответственно выпадение одного очка, двух, трех и т.д. Эти события являются несовместимыми.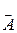 .
. или
или  , А2,..., Ак называется событие А = А
, А2,..., Ак называется событие А = А  (і =1,..., к).
(і =1,..., к). называется событие А = А
называется событие А = А  U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, называют элементарными событиями.
U2,..., Un, образующие полную группу попарно несовместимых и равновозможных событий, называют элементарными событиями.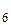 , образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1 U2,..., U
, образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U1 U2,..., U  .
.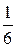 , i =l, 2,..., 6.
, i =l, 2,..., 6.
 , b
, b  3
3 

 и девочки — равновозможные события.
и девочки — равновозможные события.

 .
. Р(А)
Р(А)  , к=1,2,…n. (1.15)
, к=1,2,…n. (1.15) pi (i = 1, 2,..., k). Поэтому
pi (i = 1, 2,..., k). Поэтому получим P(
получим P(
 (см.таблицу приложения 3) и, значит, P(
(см.таблицу приложения 3) и, значит, P( .
.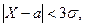 имеет вероятность, близкую к единице, т.у, является почти достоверным. Эта формула выражает так называемое правило трех сигм: если случайная величина распределена по нормальному закону распределения, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
имеет вероятность, близкую к единице, т.у, является почти достоверным. Эта формула выражает так называемое правило трех сигм: если случайная величина распределена по нормальному закону распределения, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
 ,x
,x  при условии x
при условии x  . По теореме сложения вероятностей для несовместимых событий (параграф 1.3,п.1) имеем P(X
. По теореме сложения вероятностей для несовместимых событий (параграф 1.3,п.1) имеем P(X 
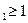 очевидно, P(X=x
очевидно, P(X=x 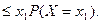 )
) 
 (2.30)
(2.30) где x
где x  .Эта сумма неотрицательна,так как x
.Эта сумма неотрицательна,так как x  . Поэтому
. Поэтому 
 x /
x /  + A arctg x/
+ A arctg x/  АП=1, откуда А=1/П.
АП=1, откуда А=1/П.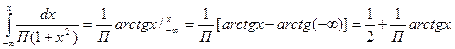
 11.Известны дисперсии двух независимых случайных величин X, Y:.
11.Известны дисперсии двух независимых случайных величин X, Y:.
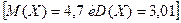

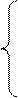
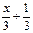 при -1<x≤2
при -1<x≤2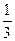 ]
]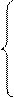
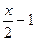 при 2<x≤4
при 2<x≤4
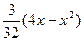 при 0≤x≤4
при 0≤x≤4 ]
]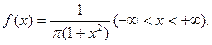
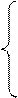 0 при x<-
0 при x<-