
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы распределения непрерывных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1.Равномерное распределение. Распределение вероятностей непрерывной случайной величины Х, принимающие все свои значения из отрезка [a;b], называются равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т.е.
Отсюда Но как известно (см.параграф 2.5, п.2), Из сравнения равенства (2.20) и (2.21)получаем c= Итак плотность вероятности непрерывной случайной величины Х, распределенной равномерно на отрезке [a;b],имеет вид Пример. На отрезке [a;b], наугад указывают точку.Какова вероятность того, что эта точка окажется в левой половине отрезка? Обозначим через Х случайную величину, равную координате выбранной точки. Х распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так как середина отрезка [a;b],имеет координату P(a<X< Впрочем, этот результат был ясен с самого начала (см.параграф 1.2, п.1). 2.Нормальный закон распределения. Закон распределения вероятностей непрерывной случайной величины Х называется нормальным законом, или законом Гаусса [1] если ее плотность вероятности есть f(x)= где Убедимся что функция (2.22)удовлетворяет условию (2.17). Действительно перейдя в интеграле К новой переменной t= Получим интеграл Но Следовательно, Значит интеграл (2.23)тоже равен единице.
Последняя сумма распространена на все значения x1 принимаемые случайной величиной X. Следовательно (см. § 2.2, п. 1),
Отсюда, сопоставляя соотношения (2.30) и (2.31), получаем искомое неравенство (2.29). Теорема. Для любой случайной величины X при каждом положительном числе г имеет место неравенство (2.32)
Неравенство (2.32) называется неравенством Чебышева*. Доказательство. Так как событие
ТО
Случайная величина неотрицательна,и, значит, согласно лемме, свойству 2 математического ожидания (§ 2.2, п. 2) и определению дисперсии (§ 2.3, п. 1)
Поэтому
Пример. Пусть случайная величина X имеет D(X)= 0,001. Какова вероятность того, что она отличается от М(Х) более чем на 0,1? По неравенству Чебышева
Примечание. Отметим другую форму неравенства Чебышева. Так как событие, выражаемое неравенством
* П. Л. Чебышев (1821 —1894) — выдающийся русский математик. (64)
Отсюда с учетом неравенства (2.32) получаем такую форму неравенства Чебышева:
2. Закон больших чисел Чебышева. Докажем закон больших чисел в широкой и удобной для практики форме, полученной П.Л. Чебышевым. Теорема (теорема Чебышева; закон больших чисел). Если дисперсии независимых случайных величин Х]у Х2,..., Хп ограничены одной и той же постоянной с,D(X1)≤ с, i= 1, 2,..., п,, то каково бы ни было
будет сколь угодно близка к единице, если число случайных величин n достаточно велико, т. е.
Доказательство. Применяя неравенство Чебышева (2.33) к величине X, имеем
Отсюда с учетом неравенства (2.35) и того, что вероятность любого события не превосходит единицы (§ 1, п. 3), получим
Наконец, переходя в неравенстве (2.36) к пределу при n→∞,приходим к искомому соотношению (2.34). Частный случай теоремы Чебышева. Если все Хк имеют одинаковое математическое ожидание М(Х1) =... = М(Хn) = а и D(Хk)<с, k= 1,..., n, то
Действительно, в условиях рассматриваемого частного случая равенство (2.34) имеет вид (2.37).
Теорема Чебышева имеет громаднейшее практическое значение. Пусть, например, измеряется некоторая физическая величина. Обычно принимают в качестве искомого значения измеряемой величины среднее арифметическое результатов нескольких измерений. Можно ли считать такой подход верным? Теорема Чебышева (ее частный случай) отвечает на этот вопрос положительно. На теореме Чебышева основан широко применяемый в статистике выборочный метод, согласно которому по сравнительно небольшой случайной выборке выносят суждение, касающееся всей совокупности исследуемых объектов. Из теоремы Чебышева (частный случай) следует теорема Бернулли, являющаяся простейшей формой закона больших чисел. Теорема Бернулли. Пусть m —число наступлений события А в n независимых испытаниях и p есть вероятность наступления события А в каждом из испытаний. Тогда, каково бы ни было положительное число
(2,38)
Доказательство. Обозначим через Xk случайную величину, равную числу наступлений события А в k-м испытании, где k=1, 2,..., п. Тогда имеем (§ 2.4, п. 1) m = Х1 + Х2 +... + Хn;
и все условия частного случая теоремы Чебышева выполнены. Равенство (2.37) превращается в равенство (2.38). Практический смысл теоремы Бернулли следующий: при постоянстве вероятности случайного события А во всех испытаниях при неограниченном возрастании числа испытаний можно с вероятностью, сколь угодно близкой к единице (т. е. как угодно близко к достоверности), утверждать, что наблюдаемая относительная частота случайного события будет как угодно мало отклоняться от его вероятности. § 2.9. Предельные теоремы теории вероятностей 1. Центральная предельная теорема. Как уже отмечалось, нормально распределенные случайные величины имеют широкое распространение на практике. Объяснение этому дает центральная предельная теорема, один из вариантов формулировки которой принадлежит русскому математику А. М. Ляпунову (1857—1918). Суть центральной предельной теоремы состоит в следующем: если случайная величина X представляет собой сумму очень большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному. Приведем без доказательства (доказательство см. в работе [3]) центральную предельную теорему для случая одинаково распределенных случайных величин. Теорема. Если Х1, Х2..., Хn —независимые случайные величины, имеющие одно и то же распределение с математическим ожиданием α и дисперсией σ2, то при неограниченном увеличении n закон распределения суммы Х=Х1 + Х2 +... + Хn неограниченно приближается к нормальному. 2. Локальная и интегральная предельные теоремы Лапласа.
Локальная предельная теорема Лапласа. Пусть р= Р(А) — вероятность события А, причем 0<p<1. Тогда вероятность того, что в условиях схемы Бернулли событие А при n испытаниях появится точно m раз, выражается приближенной формулой
где q=1-p;
Для функции φ(х) составлена таблица (см. приложение 2) ее значений для положительных значений х [функция φ (х) четная]. Выражение (2.39) называют формулой Лапласа.
Здесь p = 0,2, q=0,8, n=100 и m = 20. Отсюда, и, следовательно
Учитывая, что φ (0) = 1/
Перейдем к интегральной теореме Лапласа. Поставим следующий вопрос: какова вероятность того, что в условиях схемы Бернулли событие А, имеющее вероятность Р(А) =р(0<р< 1) при n испытаниях (как и прежде число испытаний велико), появится не менее k раз и не более l раз? Эту искомую вероятность обозначим Рn(k,l).
(2.40) Получим приближенную формулу Лапласа для подсчета суммы (2.40) при больших m и n. Используя локальную теорему Лапласа, приближенно будем иметь
где
Далее, в силу равенства (2.41) имеем
(2.42)
(2.43)
(2.44)
Выражение (2.43) при условии (2.44) и составляет содержание интегральной предельной теоремы Лапласа. Нами уже была введена функция
(2.45) называемая функцией Лапласа, или интегралом вероятности. Очевидно, Ф(х) есть первообразная для функции φ(х). Поэтому на основании формулы Ньютона — Лейбница из формулы (2.43) получим
(2.46)
Как известно, интеграл не берется в элементарных функциях. Поэтому для функции (2.45) составлена таблица (см. приложение 3) ее значений для положительных значений х, так как
(t=-z, dt=-dz) Пример 2. Вероятность того, что изделие не прошло проверку ОТК, р = 0,2. Найдем вероятность того, что среди 400 случайно отобранных изделий окажутся непроверенными от 70 до 100. Здесь n = 400, k=70, l=100, p = 0,2, q = 0,8. Поэтому в силу равенств (2.44) хk=-1,25, xl = 2,5 и, согласно формуле (2.46),
Замечание: Отметим, что локальную и интегральную предельные теоремы Лапласа иногда еще называют локальной и интегральной предельными теоремами Муавра*— Лапласа. 3. Распределение случайных ошибок измерения. Пусть проводится измерение некоторой величины. Разность х-a между результатом измерения х и истинным значением а измеряемой величины называется ошибкой измерения. Вследствие воздействия на измерение большого количества факторов, которые невозможно учесть (случайные изменения температуры, колебание прибора, ошибки, возникающие при округлении и т. п.), ошибку измерения можно считать суммой большого числа независимых случайных величин, которая по центральной предельной теореме должна быть распределена нормально. Если при этом нет систематически действующих факторов (например, неисправности приборов, завышающих при каждом измерении показания), приводящих к систематическим ошибкам, то математическое ожидание случайных ошибок равно нулю. Итак, принимается положение: при отсутствии систематически действующих факторов ошибка измерения есть случайная величина (обозначим ее через T), распределенная нормально, причем ее математическое ожидание равно нулю, т. е. плотность вероятности величины Т равна
где σ — среднеквадратическое отклонение величины Т, характеризующее разброс результатов измерения вокруг измеряемой величины. Результат измерения также есть случайная величина (обозначим ее через X), связанная с T зависимостью Х= α + Т. Отсюда: М(Х) = α, σ (Х) = σ (Т) = σ и X имеет нормальный закон распределения. Заметим, что случайная ошибка измерения, как и результаты измерения, всегда выражается в некоторых целых единицах, связанных с шагом шкалы измерительного прибора; в теории удобнее считать случайную ошибку непрерывной случайной величиной, что упрощает расчеты. При измерении возможны две ситуации: а) известно σ (это характеристика прибора и комплекса условий, при которых проводятся измерения), требуется по результатам б) σ не известно, требуется по результатам измерений оценить Рассмотрению этих ситуаций при проведении физических измерений будет посвящен § 4.3 Упражнения 1. Пусть случайная величина X— число очков, выпавших при подбрасывании игральной кости. Найдите закон распределения случайной величины X.
2. В денежной лотерее выпущено 100 билетов. Разыгрываются 1 выигрыш в 500 р. и 10 выигрышей по 10 р. Найдите закон распределения случайного выигрыша X для владельца одного лотерейного билета.
3. Закон распределения случайной величины X задан таблицей:
Найдите математическое ожидание случайной величины X. [2,2] 4. Найдите математическое ожидание выигрыша X в упражнении 2. [6 р.] 5. Найдите математическое ожидание случайной величины X, зная
[3,9] 6. Проводятся 2 выстрела с вероятностями попадания в цель, равными p1 = 0,4; p2 = 0,3. Найдите математическое ожидание общего числа попаданий. [0,7] 7. Найдите математическое ожидание суммы числа очков, которые могут выпасть при одном бросании двух игральных костей. [7] 8. Найдите математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей. [12,25] 9. Независимые случайные величины X и Y заданы следующими за
И
Найдите математическое ожидание случайной величины XY. [32,56] 10. Найдите дисперсию случайной величины X, которая задана следующим законом распределения:
[2,01]
Найдите дисперсию суммы этих величин. [7] 12.Дисперсия случайной величины X равна 5. Найдите дисперсию следующих величин: а)X-1; б) -2Х; в)3X+6. [а) 5; б) 20; в) 45] 13—15. Найдите математическое ожидание и дисперсию случайных величин, заданных различными законами распределения: 13.
14.
15.
16. К случайной величине прибавили постоянную α. Как при этом [а) прибавится α; б) не изменится ] 17. Случайную величину умножили на α. Как при этом изменятся: [а) умножится на α; б) умножится на α2]
18. Случайная величина X принимает только 2 значения: 1 или -1, каждое с вероятностью 0,5. Найдите дисперсию D(Х) и среднее квадратическое отклонение σ(Х). [D(X) = 1; σ(x)=1] 19. Дисперсия случайной величины D(Х) = 6,25. Найдите среднее квадратическое отклонение σ(Х). [2,5] 20.Пусть закон распределения случайной величины X задан таблицей:
Определите математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение σ(Х). [M(X)=11;D(X)=33;σ(X)≈5,75] 21. Дискретная случайная величина X задана законом распределения:
Найдите начальные моменты первого и второго порядков. [ν1=4,6; ν2 = 21,8] 22. Дискретная случайная величина X задана законом распределения, приведенным в предыдущем примере. Найдите центральный момент второго порядка. [μ2 = 0,64] 23.Случайная величина X задана функцией распределения
0 при x≤-1 F(x)=
1 при x>2 Найдите вероятность того, что в результате испытания случайная величина X примет значение, заключенное в интервале (0; 1). [ 24.Случайная величина X задана функцией распределения
0 при x≤2 F(x)= 1 при x>4 Найдите вероятность того, что в результате испытания X примет значение, [0,5] 25. Случайная величина X задана плотностью вероятности
0 при x<0 f(x)= 0 при x>4
Найдите вероятность попадания случайной величины X на отрезок [-2; 3]. [ 26. Плотность вероятности случайной величины X задана выражением
Найдите вероятность того, что величина X попадает на интервал (-1; 1). [0,5] 27. Случайная величина задана плотностью вероятности
f(x)= α cos x при - 0 при x> Найдите коэффициент α. [а = 0,5]
28. Дана дифференциальная функция распределения непрерывной случайной величины X
Найдите интегральную функцию распределения F(x).
29. Дана дифференциальная функция распределения непрерывной случайной величины X
Найдите интегральную функцию распределения F(x).
30. Функция
является плотностью вероятности случайной величины X. Найдите коэффициент А и функцию распределения F(x).
31. Найдите математическое ожидание случайное величины X, заданной плотностью вероятности
32. Случайная величина X задана плотностью вероятности
Найдите математическое ожидание и дисперсию случайной величины X.
33. В хлопке 75% длинных волокон. Какова вероятность того, что среди взятых наудачу трех волокон окажутся 2 длинных волокна?
34. При некоторых условиях стрельбы вероятность попадания в цель равна 1/3. Проводится 6 выстрелов. Какова вероятность ровно двух попаданий?
35. Игральная кость бросается 5 раз. Найдите вероятность того, что 2 раза появится число очков, кратное трем.
36. Монета подбрасывается 5 раз. Какова вероятность того, что герб появится не менее двух раз.
37. Пусть всхожесть семян данного растения составляет 80%. Найдите вероятность того, что из трех посеянных семян взойдут: а) два; б) не менее двух.
38. По мишени проводятся 3 выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найдите закон ее распределения.
39. Принимая вероятности рождения мальчика и девочки одинаковыми, найдите вероятность того, что среди четырех новорожденных 2 мальчика.
40. Вероятность попадания в цель при стрельбе из орудия p =0,6. Найдите математическое ожидание общего числа попаданий, если проводят 10 выстрелов.
[6 попаданий]
41. Найдите математическое ожидание числа лотерейных билетов, на которое выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша по одному билету равна 0,3.
[6 билетов]
42. Найдите дисперсию случайной величины X – числа появлений события А в 100 независимых испытаниях, в каждом из которых вероятность наступления события А равна 0,7.
[21]
43. Найдите: а) математическое ожидание и б) дисперсию числа бракованных изделий в партии из 5000 изделий, если каждое изделие может оказаться бракованным с вероятностью 0,02.
[а) 100 изделий; б) 98]
44. Проводится 10 независимых испытаний, в каждом из которых вероятность появления события А равна 0,6. Найдите дисперсию случайной величины X – числа появлений события А в этих испытаниях.
[2,4]
45. Найдите дисперсию случайной величины X – числа появлений события А в двух независимых испытаниях, если M(X) =0,8.
[0,48]
46. Рост взрослой женщины является случайной величиной, распределенной по нормальному закону с параметрами: а=164 см, s=5,5. Найдите плотность вероятности этой величины.
47. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 0 и 2. Найдите вероятность того, что X примет значение, принадлежащее интервалу (-2; 3)
[0,77453]
48. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 6 и 2. Найдите вероятность того, что X примет значение, принадлежащее интервалу (4; 8).
[0,6826]
49. Пусть масса пойманной рыбы подчиняется нормальному закону с параметрами: а=375 г; s= 25 г. Найдите вероятность того, что масса пойманной рыбы будет от 300 до 425 г.
[0,9759]
50. Диаметр детали, изготовляемой в цеху, является случайной величиной, распределенной по нормальному закону. Дисперсия ее равна 0,0001, а математическое ожидание – 2,5 мм. Найдите границы, в которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали.
[2,47; 2,53]
51. Случайная величина X распределена по нормальному закону. Среднее квадратическое отклонение этой величины равно 0,4. Найдите вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине будет меньше 0,3.
[0,5468]
52. Случайная величина X распределена по нормальному закону. Среднее квадратическое отклонение этой величины равно 2. Найдите вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине будет меньше 0,1.
[0,03988]
53. Случайная величина X подчиняется нормальному закону распределения с математическим ожиданием 30 и дисперсией 100. Найдите вероятность того, что значение случайной величины заключено в интервале (10; 50).
[0,954]
54. Найдите дисперсию случайной величины X, заданной таблицей распределения:
[1,05]
55. При выработке некоторой массовой продукции вероятность появления одного нестандартного изделия составляет 0,01. Какова вероятность того, что в партии из 100 изделий этой продукции 2 изделия будут нестандартными?
[0,184]
56. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что одна деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных?
[0,003]
57. Игральную кость бросают 80 раз. Определите вероятность того, что цифра 3 появится 20 раз.
[0,0162]
58. При установившемся технологическом режиме завод выпускает в среднем 70% продукции первого сорта. Определите вероятность того, что из 1000 изделий число первосортных заключено между 652 и 760.
[0,99945]
59. Вероятность наступления случайного события при отдельном испытании равна p. Определите вероятность того, что в n испытаниях событие наступит подряд k раз.
[(n – k+ 1) ∙ p k ∙(1 – p) n-k ]
60. Подсчитайте при одновременном бросании n игральных костей количество исходов, в которых определенная грань встречается k раз.
[5 n-k
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1936; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.013 с.) |

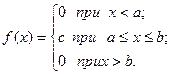

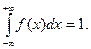
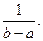
 , то искомая вероятность равна (см.параграф 2.5, п.2):
, то искомая вероятность равна (см.параграф 2.5, п.2):
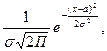 (2.22)
(2.22)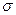 и a -постоянная, причем
и a -постоянная, причем 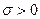 .
.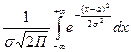 (2.23)
(2.23)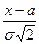 (2.24)
(2.24)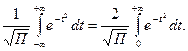
 (см.приложение 1).
(см.приложение 1).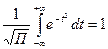 (2.25)
(2.25)

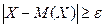 равносильно событию
равносильно событию
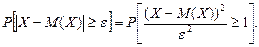
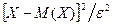
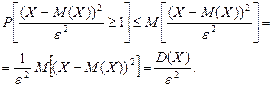
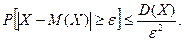

 противоположно событию, выражаемому неравенством
противоположно событию, выражаемому неравенством 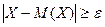 , то (§ 1.3, п. 1, следствие 2)
, то (§ 1.3, п. 1, следствие 2)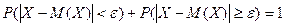
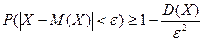 (2.33)
(2.33)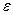 > 0, вероятность выполнения неравенства
> 0, вероятность выполнения неравенства 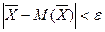 , где
, где
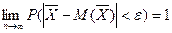 (2.34)
(2.34) (2.35)
(2.35) Пользуясь свойствами дисперсии (§ 2.3, п. 2) и условием теоремы, получим
Пользуясь свойствами дисперсии (§ 2.3, п. 2) и условием теоремы, получим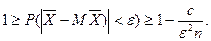 (2.36)
(2.36) (2.37)
(2.37) Сущность теоремы Чебышева состоит в следующем. Несмотря на то, что каждая из независимых случайных величин Хk может принять значение, далекое от математического ожидания М(Хk), среднее арифметическое достаточно большого числа случайных величин с большой вероятностью весьма близко к среднему арифметическому их математических ожиданий.
Сущность теоремы Чебышева состоит в следующем. Несмотря на то, что каждая из независимых случайных величин Хk может принять значение, далекое от математического ожидания М(Хk), среднее арифметическое достаточно большого числа случайных величин с большой вероятностью весьма близко к среднему арифметическому их математических ожиданий.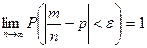

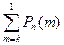 Если число испытаний п велико, то вычисления по формуле Бернулли становятся затруднительными. Лаплас* получил важную приближенную формулу для расчета вероятности Рn(m) появления события А точно m раз, если n — достаточно большое число. Им же получена приближенная формула и для суммы вида
Если число испытаний п велико, то вычисления по формуле Бернулли становятся затруднительными. Лаплас* получил важную приближенную формулу для расчета вероятности Рn(m) появления события А точно m раз, если n — достаточно большое число. Им же получена приближенная формула и для суммы вида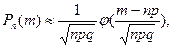 (2.39)
(2.39)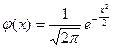
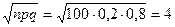 Пример 1. Вероятность поражения цели стрелком при одиночном выстреле p= 0,2. Какова вероятность того, что при 100 выстрелах цель будет поражена ровно 20 раз?
Пример 1. Вероятность поражения цели стрелком при одиночном выстреле p= 0,2. Какова вероятность того, что при 100 выстрелах цель будет поражена ровно 20 раз?
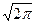 - 0,40, из формулы (2.39) получаем
- 0,40, из формулы (2.39) получаем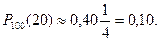
 На основании теоремы сложения вероятностей для несовместимых событий (§ 1.3, п. 1) получим
На основании теоремы сложения вероятностей для несовместимых событий (§ 1.3, п. 1) получим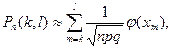
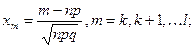 (2.41)
(2.41)
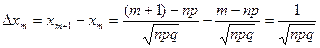
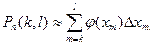 и потому
и потому
 Здесь сумма справа является интегральной суммой для функции φ(х) на отрезке причем, как следует из равенства (2.42), при
Здесь сумма справа является интегральной суммой для функции φ(х) на отрезке причем, как следует из равенства (2.42), при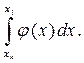 Следовательно, при n→∞ предел указанной интегральной суммы есть определенный интеграл
Следовательно, при n→∞ предел указанной интегральной суммы есть определенный интеграл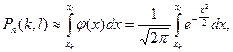 Поэтому
Поэтому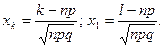 Где
Где
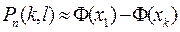
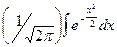 (интегральная формула Лапласа).
(интегральная формула Лапласа).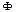 (0) = 0 и функция Ф(х) нечетная:
(0) = 0 и функция Ф(х) нечетная:
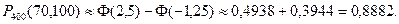
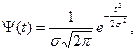
 11.Известны дисперсии двух независимых случайных величин X, Y:.
11.Известны дисперсии двух независимых случайных величин X, Y:.
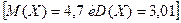

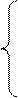
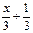 при -1<x≤2
при -1<x≤2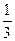 ]
]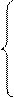
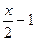 при 2<x≤4
при 2<x≤4
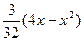 при 0≤x≤4
при 0≤x≤4 ]
]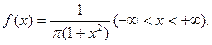
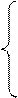 0 при x<-
0 при x<- 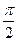
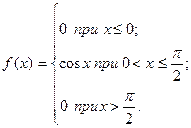
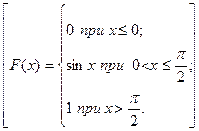
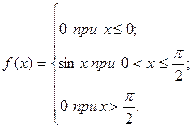
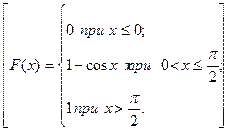

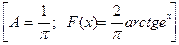
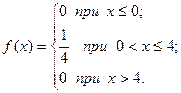
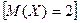
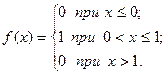

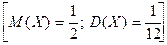
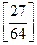



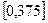
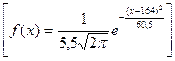
 ]
]


