
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события и случайные величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Глава 1 Описательная статистика Случайные события и случайные величины Все процессы, происходящие в природе, являются результатом взаимодействия многих факторов. Для того чтобы изучить эти процессы и в дальнейшем ими управлять, необходимо выяснить, какую роль в рассматриваемом процессе играет каждый фактор в отдельности. Так, например, изучая самочувствие больного, приходится учитывать множество факторов, как улучшающих его, так и ухудшающих. Все эти факторы необходимо выразить в каких-то количественных оценках. Таким образом, математические методы изучения взаимодействующих факторов требуют умения выражать действие различных факторов количественно. Чтобы получить необходимые числовые данные, нужно произвести серию наблюдений. Случайные, непредвиденные события в массе своей подчиняются некоторым общим неслучайным закономерностям. Наука, изучающая закономерности массовых случайных событий, называется теорией вероятностей. Применение теории вероятностей к обработке больших совокупностей чисел называется математической статистикой. Использование методов математической статистики в обработке наблюдений оказывается весьма плодотворным. Закономерности отклонений при наблюдениях изучены достаточно хорошо, составлены многочисленные таблицы. Это позволяет значительно сокращать объем наблюдений. Но случайность остается случайностью, и никакие теории при наличии непредвиденных и случайных факторов не могут давать точные и однозначные ответы. Основная задача математической статистики при обработке наблюдений – оценить риск той или иной ошибки в полученном результате. Основу изучения различных процессов, происходящих в природе, составляет выяснение всевозможных причинно – следственных связей между отдельными явлениями путем эксперимента. Событие, которое при заданном комплексе факторов обязательно произойдет, называется достоверным событием. Например, восход и закат Солнца есть события достоверные. Событие, которое не может осуществиться при заданном комплексе факторов, называется невозможным событием. Так, невозможным событием является электрический ток в цепи при отсутствии в ней источника тока. Событие, которое при заданном комплексе факторов может либо произойти, либо не произойти, называется случайным событием. В дальнейшем вместо слов «случайное событие» употребляется просто термин «событие». С примерами случайных событий мы встречаемся на каждом шагу, если задаемся вопросами: какой номер автобуса раньше подойдет к остановке, на которой мы ожидаем; выпадет ли завтра дождь; какой стороной упадет подброшенная вверх монета – везде, где отсутствует полная информация, появляется случайность. Для того чтобы выяснить, произойдет или не произойдет некоторое событие при заданном комплексе основных факторов, нужно, прежде всего, осуществить этот комплекс. Каждое такое осуществление принято называть испытанием. Испытанием является, в частности, любой эксперимент, в результате которого производятся наблюдения. Ожидание автобуса, подбрасывание монеты в приводившихся примерах – тоже испытания. Предсказать результат единичного испытания можно лишь для достоверных или невозможных событий. Случайность же события вообще не видна при единичном испытании: если событие произойдет, оно может показаться нам достоверным, если не произойдет – невозможным. Теория случайных событий может появиться лишь при большом числе испытаний, лишь для массовых событий. Важным условием при этом является неизменность заданного комплекса основных факторов. События, происходящие при одном и том же комплексе основных факторов, называются однородными. Практика показывает, что события, сами по себе случайные, в большой массе при наличии однородности начинают подчиняться некоторым неслучайным закономерностям. Понятие случайной величины Интерес к изучению случайных событий связан в первую очередь с тем, что именно к ним относятся результаты большинства наблюдений. Даже самый точный метод анализа дает при повторениях некоторое расхождение в результатах (ошибку воспроизводимости), значит, здесь каждый числовой результат есть случайное событие. Случайными являются содержание сахара или гормонов в крови, рост и вес обследуемых пациентов и т.д. В медицине и биологии рассматривают объект наблюдения, например, больного. В процессе наблюдения выявляют пол больного, состояние заболевания, рост, вес, количественные данные лабораторных исследований и т.д. Отдельные параметры, например пол, являются качественными, другие, например рост, являются количественными. Рассмотренные примеры приводят нас к важному понятию случайной величины. Случайной величиной называется величина, принимающая в результате испытания определённое значение, которое нельзя предсказать, исходя из условий испытания. Случайная величина обладает целым набором допустимых значений, но в результате каждого отдельного испытания принимает лишь какое-то одно из них. Очень важно отметить, что случайная величина может принимать различные значения при неизменном комплексе основных факторов. Причина её изменения от испытания к испытанию кроется в не учитываемых нами факторах, которые мы назвали случайными. Случайные величины подразделяют на дискретные и непрерывные. Дискретные случайные величины принимают строго определенные значения и других значений между ними быть не может. Непрерывные случайные величины принимают любое значение в заданном интервале. Таблица 1.1 Типы шкал
Мы видим, что кодирование переменной пол с помощью цифр 1 и 2 абсолютно произвольно, их можно было поменять местами или обозначить другими цифрами. Это не значит, что женщины стоят на ступеньку ниже мужчин. В этом случае говорят о переменных, относящихся к номинальной шкале. Такая же ситуация и с переменной семейное положение. Здесь также соответствие между числами и категориями семейного положения не имеет никакого эмпирического значения. Но в отличии от пола, эта переменная не является дихотомической - у нее четыре кодовых цифры вместо двух. Переменная курение отсортирована в порядке значимости снизу вверх: умеренный курильщик курит больше, нежели некурящий, а сильно курящий - больше, чем умеренный курильщик и т.д. Эти переменные относятся к порядковой шкале. Однако эмпирическая значимость этих переменных не зависит от разницы между соседними численными значениями. Так, несмотря на то, что разница между значениями кодовых чисел для некурящего, редко курящего и интенсивно курящего в обоих случаях равна единице, нельзя утверждать, что фактическое различие между некурящим, изредка курящим и интенсивно курящим одинаково. Для этого данные понятия слишком расплывчаты. Классическими примерами переменных с порядковой шкалой являются также переменные, полученные в результате объединения величин в классы, такие, как месячный доход в нашем примере. Рассмотрим теперь коэффициент интеллекта (IQ). И его абсолютные значения отображают порядковое отношение между респондентами, и разница между двумя значениями также имеет эмпирическую значимость. Например, если у Федора IQ равен 80, у Петра – 120 и у Ивана – 160, можно сказать, что Петр в сравнении с Федором настолько же интеллектуальнее насколько Иван в сравнении с Петром (а именно – на 40 единиц IQ). Однако, основываясь только на том, что значение IQ у Федора в два раза меньше, чем у Ивана, нельзя сделать вывод, что Иван вдвое умнее Федора. Такие переменные относятся к интервальной шкале. Наивысшей статистической шкалой, на которой эмпирическую значимость приобретает и отношение двух значений, является шкала отношений. Примером переменной, относящейся к такой шкале, является возраст: если Андрею 30 лет, а Алексею 60, можно сказать, что Алексей вдвое старше Андрея. Шкалой отношений является температурная шкала Кельвина с абсолютным нулём температур. На практике, в том числе при обработке данных в пакете Statistica, различие между переменными, относящимися к интервальной шкале и шкале отношений обычно несущественно. От более богатой или мощной шкалы всегда можно перейти к более бедной. Так, непрерывные переменные можно категоризировать. Например, непрерывную случайную величину (СВ) Рост можно из шкалы отношений перевести в порядковую шкалу с градациями: низкий, средний, высокий. Допустим, весь диапазон изменения интервальной переменной был разделен на область высоких, средних и низких значений и каждое наблюдение было отнесено к одной из трех категорий. Это означает, что явление, которое вначале описывалось в интервальной шкале, может быть описано также и в шкале наименований, а, следовательно, можно использовать для анализа этого явления все те статистические методы, которые требуют использования переменных в шкале наименований. Но надо учитывать, что при переходе к шкале наименований от шкал более высокого порядка, мы теряем часть информации о наблюдениях. Наблюдения, которые отличались друг от друга при описании их в интервальной шкале, могут восприниматься как одинаковые при описании их в шкале наименований. Поэтому рекомендуется применять шкалу наименований лишь тогда, когда нет возможности использовать шкалу более высокого порядка. Таблица 1.2 Вариационный ряд
В отличие от исходных данных этот ряд позволяет делать некоторые выводы о статистических закономерностях. Если число возможных значений дискретной случайной величины достаточно велико или наблюдаемая случайная величина является непрерывной, то строят интервальный вариационный ряд, под которым понимают упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частностями попаданий в каждый из них значений случайной величины. Как правило, частичные интервалы, на которые разбивается весь интервал варьирования, имеют одинаковую длину и представимы в виде
Длину ∆x следует выбирать так, чтобы построенный ряд не был громоздким, но в то же время позволял выявлять характерные изменения случайной величины. Рекомендуется для ∆x использовать следующую формулу
Число интервалов определяют по формуле Стерджесса: Если окажется, что ∆x – дробное число, то за длину интервала следует принять либо ближайшую простую дробь, либо ближайшую целую величину. При этом необходимо выполнение условий:
После нахождения частных интервалов определяется, сколько значений случайной величины попало в каждый конкретный интервал. При этом в интервал включают значения большие или равные нижней границе и меньшие верхней границы. Пример 2. [3]: При изменении диаметра валика после шлифовки была получена следующая выборка (объемом n=55):
Решение. Так как наибольшая варианта равна 23.8, а наименьшая 10.1, то вся выборка попадает в интервал (10, 24). Мы расширили интервал (10.1, 23.8) для удобства вычислений. По формуле Стерджесса получим семь частичных интервалов. Длина каждого частичного интервала равна В результате весь диапазон данных разделяется на следующие интервалы:
Соответствующий интервальный вариационный ряд называют сгруппированным, он представлен в следующей таблице: Таблица 1.3 Полигон. Гистограмма Второй способ задания случайной величины – графический. На графике для дискретной случайной величины откладываются ее значения и частоты появления или частости. Если данные точки соединить между собой, мы получим график в виде ломаной линии. Он называется полигоном (Рис. 1.1). В случае сгруппированного вариационного ряда для дискретной и непрерывной случайной величины на графике откладываются интервалы ее значений ∆xi и частоты mi или частости Pi=
Рис. 1.1 Плотностью вероятности называют отношение вероятности появления случайной величины к интервалу значений, в котором она появляется: Отсюда вытекает соотношение: Pi=fi∆xi. Т.е. вероятность равна площади прямоугольника высотой fi и шириной ∆xi (заштрихованная область на Рис. 1.3).
Рис. 1.2
Гистограмма и полигон грубо задают распределение случайной величины. Гистограмма и полигон могут быть построены как для дискретной, так и для непрерывной случайной величины. На практике чаще для дискретной случайной величины строят полигон, а для непрерывной – гистограмму.
Рис. 1.3
Очевидно, предположить, что при уменьшении ширины интервала график будет принимать вид плавной кривой (Рис.1.4), которую, как и любую кривую, можно представить в виде формулы, т.е. аналитически.
Рис. 1.4
Распределение случайной величины может описываться аналитически с помощью различных формул. В зависимости от того, какова эта формула, какие параметры в неё входят, распределение носит определенное название: Пуассона, Максвелла, биноминальное, экспоненциальное и т.д. Число всевозможных типов распределений очень велико. Однако на практике далеко не все распределения встречаются одинаково часто. Анализ различных случайных величин, как изучаемых теоретически, так и вычисляемых на основании опытов, показывает существование одного наиболее часто встречающегося распределения, называемого нормальным. Большинство случайных величин в медицине и биологии подчиняется именно нормальному закону распределения. А б Рис. 1.10 Если интервал расположен симметрично относительно центра нормального распределения (относительно математического ожидания а), так что влево и вправо взяты одинаковые отрезки ∆x (Рис. 1.10.б), то ширина интервала будет 2∆x. Иногда в решении задач доверительным интервалом называют полуширину ∆x. Границы интервала можно обозначить как α и β. Каждому доверительному интервалу ставится в соответствие доверительная вероятность Р или надежность. Эта оценка позволяет ответить на вопрос, какой вероятностью находится неизвестное значение оцениваемого параметра генеральной совокупности внутри заданного интервала. И пусть мы не сможем точно указать, где на числовой оси находится неизвестный параметр, но мы можем указать доверительный интервал 2∆x, в котором он находится с доверительной вероятностью Р. Функция Лапласа. Для решения задачи интервального оценивания перейдем от переменной x к переменной t в функции Гаусса. Пусть (х–а) фактическое отклонение отдельного значения случайной величины от математического ожидания. Разделим его на стандартное отклонение σ. Обозначим результат деления как Используя параметр t, можно произвести замену переменной в функции Гаусса Значения данного интеграла для разных t вычислил Лаплас и представил их в виде таблицы. Эту таблицу можно найти в любом математическом справочнике. Поскольку значения этого интеграла зависят от предела t, то интеграл от функции Гаусса стали называть функцией Лапласа и обозначать как Замечание. Иногда в таблицах нормального распределения вместо функции Лапласа указывается сама вероятность Р или уровень значимости α, параметр t может иметь обозначение z.
Рис. 1.11
Доверительный интервал для отдельных значений изучаемого признака при известном параметре σ Пусть генеральная совокупность Х распределена по нормальному закону N(a,σ), причем, параметр σ известен. Необходимо оценить доверительный интервал для самих значений измеряемого признака. В этом случае из формулы Его центр находится в точке a, левая граница имеет значение Вариант 1 Пусть необходимо определить интервальную оценку для математического ожидания a с заданной доверительной вероятностью длянормально распределенной генеральной совокупности Х в том случае, когда генеральная дисперсия D неизвестна, а выборка имеет небольшой объем. Иначе говоря, будем решать задачу о том, насколько точно мы с помощью выборочного среднего оценили математическое ожидание случайной величины, насколько они отличаются друг от друга. · По условию задачи необходимо определить · Вычислить степень свободы k=n-1. По k и заданной доверительной вероятности Р в таблице Стьюдента выбирается tp,k. · Вычислить по выборке стандартное отклонение · Определить полуширину доверительного интервала по формуле: или Определить границы доверительного интервала: α= Т.о. критерий Стьюдента позволяет найти предельную случайную ошибку оценки математического ожидания при заданной доверительной вероятности (или уровне значимости), зная стандартную ошибку по выборочным данным и коэффициент tp,k. Вариант 2 Пусть необходимо по заданному доверительному интервалу (его полуширине) · По условию задачи определить · По известному значению или · Вычислить степень свободы k=n-1. · Определить доверительную вероятность (или уровень значимости) по таблице Стьюдента, остановившись на равном или ближайшем меньшем значении tp,k в таблице на строке k. Значение доверительной вероятности Р или уровня значимости Глава 1 Описательная статистика Случайные события и случайные величины Все процессы, происходящие в природе, являются результатом взаимодействия многих факторов. Для того чтобы изучить эти процессы и в дальнейшем ими управлять, необходимо выяснить, какую роль в рассматриваемом процессе играет каждый фактор в отдельности. Так, например, изучая самочувствие больного, приходится учитывать множество факторов, как улучшающих его, так и ухудшающих. Все эти факторы необходимо выразить в каких-то количественных оценках. Таким образом, математические методы изучения взаимодействующих факторов требуют умения выражать действие различных факторов количественно. Чтобы получить необходимые числовые данные, нужно произвести серию наблюдений. Случайные, непредвиденные события в массе своей подчиняются некоторым общим неслучайным закономерностям. Наука, изучающая закономерности массовых случайных событий, называется теорией вероятностей. Применение теории вероятностей к обработке больших совокупностей чисел называется математической статистикой. Использование методов математической статистики в обработке наблюдений оказывается весьма плодотворным. Закономерности отклонений при наблюдениях изучены достаточно хорошо, составлены многочисленные таблицы. Это позволяет значительно сокращать объем наблюдений. Но случайность остается случайностью, и никакие теории при наличии непредвиденных и случайных факторов не могут давать точные и однозначные ответы. Основная задача математической статистики при обработке наблюдений – оценить риск той или иной ошибки в полученном результате. Основу изучения различных процессов, происходящих в природе, составляет выяснение всевозможных причинно – следственных связей между отдельными явлениями путем эксперимента. Событие, которое при заданном комплексе факторов обязательно произойдет, называется достоверным событием. Например, восход и закат Солнца есть события достоверные. Событие, которое не может осуществиться при заданном комплексе факторов, называется невозможным событием. Так, невозможным событием является электрический ток в цепи при отсутствии в ней источника тока. Событие, которое при заданном комплексе факторов может либо произойти, либо не произойти, называется случайным событием. В дальнейшем вместо слов «случайное событие» употребляется просто термин «событие». С примерами случайных событий мы встречаемся на каждом шагу, если задаемся вопросами: какой номер автобуса раньше подойдет к остановке, на которой мы ожидаем; выпадет ли завтра дождь; какой стороной упадет подброшенная вверх монета – везде, где отсутствует полная информация, появляется случайность. Для того чтобы выяснить, произойдет или не произойдет некоторое событие при заданном комплексе основных факторов, нужно, прежде всего, осуществить этот комплекс. Каждое такое осуществление принято называть испытанием. Испытанием является, в частности, любой эксперимент, в результате которого производятся наблюдения. Ожидание автобуса, подбрасывание монеты в приводившихся примерах – тоже испытания. Предсказать результат единичного испытания можно лишь для достоверных или невозможных событий. Случайность же события вообще не видна при единичном испытании: если событие произойдет, оно может показаться нам достоверным, если не произойдет – невозможным. Теория случайных событий может появиться лишь при большом числе испытаний, лишь для массовых событий. Важным условием при этом является неизменность заданного комплекса основных факторов. События, происходящие при одном и том же комплексе основных факторов, называются однородными. Практика показывает, что события, сами по себе случайные, в большой массе при наличии однородности начинают подчиняться некоторым неслучайным закономерностям.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.238 (0.011 с.) |









 , где k - число интервалов.
, где k - число интервалов. , где xmax, xmin – наибольшее и наименьшее значения случайной величины.
, где xmax, xmin – наибольшее и наименьшее значения случайной величины. .
. .
. .
. причем в первый интервал попадает два значения СВ, во второй – четыре и т.д.
причем в первый интервал попадает два значения СВ, во второй – четыре и т.д. . Подобный график будет грубо отражать распределение непрерывной случайной величины на числовой оси и называется гистограмма (Рис. 1.2). Если интервалы равные, то гистограмму можно строить в координатах xi ↔ mi или xi ↔ Pi .В случае, когда интервалы не равны между собой, гистограмма строится в координатах xi ↔ fi, где fi – плотность вероятности, величина, характеризующая распределение вероятности на интервале.
. Подобный график будет грубо отражать распределение непрерывной случайной величины на числовой оси и называется гистограмма (Рис. 1.2). Если интервалы равные, то гистограмму можно строить в координатах xi ↔ mi или xi ↔ Pi .В случае, когда интервалы не равны между собой, гистограмма строится в координатах xi ↔ fi, где fi – плотность вероятности, величина, характеризующая распределение вероятности на интервале.

 .
.





 . Таким образом мы нормализуем или стандартизируем все значения переменной х. Данный параметр имеет следующий смысл: он показывает, во сколько раз фактическое отклонение отличается от стандартного. Поэтому параметр t называют относительным отклонением. Его принято называть статистическим критерием стандартного нормального распределения. При проверке статистических гипотез его значения позволяют или принять или отклонить выдвинутые гипотезы.
. Таким образом мы нормализуем или стандартизируем все значения переменной х. Данный параметр имеет следующий смысл: он показывает, во сколько раз фактическое отклонение отличается от стандартного. Поэтому параметр t называют относительным отклонением. Его принято называть статистическим критерием стандартного нормального распределения. При проверке статистических гипотез его значения позволяют или принять или отклонить выдвинутые гипотезы.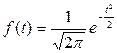 . От этого выражение становится проще, а график сдвигается в начало координат в точку с координатой t=0 (с математическим ожиданием равным нулю и σ =1) с границами интервала – t и + t (Рис. 1.11). С таким графиком удобнее работать, так как множество различных случайных величин с нормальным распределением могут быть представлены однообразным графиком и появляется возможность создать единый алгоритм решения задач для самых разных СВ. Как уже было сказано выше, вероятность попадания значения случайных величин в заданный интервал равна площади под кривой функции плотности вероятности над данным интервалом. На Рис. 1.11 эта площадь заштрихована. В математике площадь, лежащая под графиком некоторой функции, равна интегралу от этой функции. Тогда для нахождения вероятности попадания значения случайных величин в интервал от – t до + t, проинтегрируем функцию плотности вероятности в данных пределах.
. От этого выражение становится проще, а график сдвигается в начало координат в точку с координатой t=0 (с математическим ожиданием равным нулю и σ =1) с границами интервала – t и + t (Рис. 1.11). С таким графиком удобнее работать, так как множество различных случайных величин с нормальным распределением могут быть представлены однообразным графиком и появляется возможность создать единый алгоритм решения задач для самых разных СВ. Как уже было сказано выше, вероятность попадания значения случайных величин в заданный интервал равна площади под кривой функции плотности вероятности над данным интервалом. На Рис. 1.11 эта площадь заштрихована. В математике площадь, лежащая под графиком некоторой функции, равна интегралу от этой функции. Тогда для нахождения вероятности попадания значения случайных величин в интервал от – t до + t, проинтегрируем функцию плотности вероятности в данных пределах. 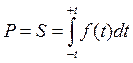 . Учитывая симметричность интервала, найдем площадь от 0 до t и умножим на два.
. Учитывая симметричность интервала, найдем площадь от 0 до t и умножим на два. 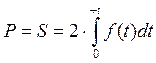 . Подставим в данное выражение функцию Гаусса.
. Подставим в данное выражение функцию Гаусса. 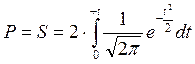 .
.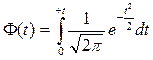 . Таким образом, вероятность нахождения неизвестного значения оцениваемого параметра генеральной совокупности можно найти по формуле: Р=2Ф(t). Если интервал несимметричен P=Ф(t2) – Ф(t1)
. Таким образом, вероятность нахождения неизвестного значения оцениваемого параметра генеральной совокупности можно найти по формуле: Р=2Ф(t). Если интервал несимметричен P=Ф(t2) – Ф(t1)

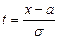 или
или 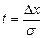 выводим формулу доверительного интервала для отдельных значений СВ. Полуширина доверительного интервала
выводим формулу доверительного интервала для отдельных значений СВ. Полуширина доверительного интервала 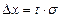
 , правая граница
, правая граница 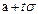 , а длина интервала 2tσ.
, а длина интервала 2tσ. .
. или стандартную ошибку
или стандартную ошибку 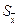


 х, β=
х, β= 

 будет указано вверху столбца.
будет указано вверху столбца.


