Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смысл сигмового, двухсигмового и трехсигмового интервалов.Содержание книги
Поиск на нашем сайте Найдем вероятность того, что нормально распределенная величина будет отклоняться от математического ожидания на величину: · стандартного отклонения, т.е. P( · двойного стандартного отклонения, т.е. P( · тройного стандартного отклонения, т.е. P( Из данных уравнений мы делаем вывод, что при нормальном распределении 68% всех значений случайной величины лежит в пределах стандартного отклонения. Если отклонение равно двум стандартным отклонениям, то в пределах такого интервала лежит почти 95% значений случайной величины, в хвосты попадает менее 5% значений. И, наконец, при трехсигмовом интервале в нём заключено 99% всех значений, а в хвосты попадает лишь 1% значений переменной. В медицинской практике обычно доверительный интервал отдельных значений определяют как выборочное среднее плюс-минус два стандартных отклонения, что очень важно при выяснении того, попадает ли анализ какого-либо пациента в «норму» или нет. Практическое применение s в биологических науках не ограничивается лишь сферой морфологических и анатомических исследований. Этот показатель хорошо зарекомендовал себя при упорядочивании представлений о сезонных явлениях в природе, о распределении и динамике численности организмов, а также при решении вопросов селекции и генетики. Таким образом, стандартное отклонение представляет собой одну из наиболее обоснованных и эффективных описательных статистик. Однако, если необходимо сопоставить изменчивость признаков, представленных в разных единицах измерения (например, мм и г) этот показатель использовать нельзя, так как он измеряется в тех же величинах, что и средняя величина. Кроме того, одно и то же значение стандартного отклонения (например, s = 2) может указывать как на очень малую (при
Чем меньше коэффициент вариации, тем однороднее выборка. Варьирование считается слабым, если не превосходит 10%. Если коэффициент вариации 10-20%, то это среднее варьирование. Сильным оно считается при Cv>20%. Статистическими исследованиями установлено, что изменчивость одного и того же признака, выраженная коэффициентом вариации, может отличаться как у различных видов, так и у разных популяций в пределах одного вида, причём эти отличия зачастую не случайны и имеют направленный характер. Это послужило основой для формирования единых методологических позиций при изучении индивидуальной и эволюционной изменчивости организмов. Интересные результаты, например, получены на основе анализа большого материала по изменчивости морфофизиологических признаков птиц. Оказалось, что у некоторых видов степень вариабельности интерьерных признаков четко отличается у северных и южных популяций, тогда как изменчивость индексов ряда внутренних органов не совпадает с географическими градиентами. Последнее объясняется функциональным значением внутренних органов. Например, в любой географической зоне требуется строго определённое соотношение массы тела и массы летательной мускулатуры у всех слагающих популяцию особей. Коэффициент вариации находит применение и в селекционной работе. Например, при сравнении двух сходных по продуктивности и качественным показателям сортов, предпочтение должно быть отдано тому из них, который при равных условиях обладает меньшей изменчивостью. При оценке пригодности того или иного количественного метода принимают во внимание два основных критерия. Во-первых, точность, которая представляет собой степень отклонения результатов от истинных значений (о ней речь пойдет дальше), и, во-вторых, воспроизводимость, отражающую степень идентичности величин, получаемых при повторных определениях какого-то компонента в одном образце. Воспроизводимость оценивают по коэффициенту вариабельности между разными анализами и в пределах одного анализа. Например, определяется воспроизводимость двух методов измерения СОЭ. Первый метод (модифицированный метод Вестергрина) дал величину σ = 1,0 мм при Непосредственное сравнение средних квадратичных отклонений не дает ответа, так как речь идет о двух величинах, выраженных в разных единицах измерения. Следовательно, необходимо прибегнуть к коэффициенту вариации: V1=(1/10)*100=10%; V2=(15/180)*100=8,33%. Вывод: Воспроизводимость первого проверяемого метода ниже по сравнению со вторым (10% > 8,33%). В американских специализированных клиниках были проведены программные обследования населения. При статистической обработке результатов более чем десятилетней работы по определению концентраций холестерина и триглицеридов химическими методами было показано, что коэффициенты вариабельности составляют, соответственно, <3% и 4%. Сходную воспроизводимость удается достичь и в случае автоматизированного анализа, основанного на использовании ферментативных методов. Согласно последним рекомендациям американской Национальной программы по изучению холестерина, коэффициенты вариабельности при проведении анализов не должны превышать 5%. Коэффициент вариации используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Интервальные оценки с использованием распределения Стьюдента при неизвестном σ Разработка теории малой выборки была начата английским статистиком В.С. Госсетом (печатавшимся под псевдонимом Стьюдент) в 1908 г. Он доказал, что в малой выборке действует особый закон распределения. При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента. Согласно распределению Стьюдента, доверительный интервал зависит как от доверительной вероятности Р, так и от объема выборки n. Чем меньше объем выборки, тем более случайным образом, а значит, менее надежно располагается в данном интервале неизвестный параметр. Распределение таких выборок описывается формулой Госсета
Значения этой функции, как видно, зависят от t и k. Параметр k называется числом степеней свободы. Эта величина мало отличается от числа опытов n. Для разных задач k=n-1, k=n-2, k=2(n-1). При увеличении k→∞, а значит, числа опытов n →∞, значения функции Госсета приближается к значениям функции Гаусса, а график распределения Стьюдента стремится принять вид графика нормального распределения. При малых значениях опытов график Стьюдента пологий, «размытый». Это можно объяснить тем, что при одном и том же значении t, но разных n, вероятность будет разной. Поскольку вероятность численно равна площади криволинейной трапеции, то высота графиков окажется разной при разных t. Но общая площадь под любой трапецией одинакова, поскольку вероятность попасть в интервал от -∞ до +∞ в любом случае равна 1 (или 100%).
Рис. 1.12
Для выборок малого объема значения параметра t для разных n и разных доверительных вероятностей Р (или уровней значимости При этом можно обратить внимание на то, что при больших вероятностях при уменьшении выборки, значения t возрастают более резко, чем при малых вероятностях, а значит резко будет расширяться интервал. В силу двух последних обстоятельств параметр Стьюдента может иметь обозначение tp,k. Замечание. При достаточно большом объёме выборки на строке, обозначаемой в таблице Стьюдента значком бесконечности (∞) значения параметра tp,k совпадают со значениями t из таблицы Лапласа при такой же вероятности. Вариант 1 Пусть необходимо определить интервальную оценку для математического ожидания a с заданной доверительной вероятностью длянормально распределенной генеральной совокупности Х в том случае, когда генеральная дисперсия D неизвестна, а выборка имеет небольшой объем. Иначе говоря, будем решать задачу о том, насколько точно мы с помощью выборочного среднего оценили математическое ожидание случайной величины, насколько они отличаются друг от друга. · По условию задачи необходимо определить · Вычислить степень свободы k=n-1. По k и заданной доверительной вероятности Р в таблице Стьюдента выбирается tp,k. · Вычислить по выборке стандартное отклонение · Определить полуширину доверительного интервала по формуле: или Определить границы доверительного интервала: α= Т.о. критерий Стьюдента позволяет найти предельную случайную ошибку оценки математического ожидания при заданной доверительной вероятности (или уровне значимости), зная стандартную ошибку по выборочным данным и коэффициент tp,k. Вариант 2 Пусть необходимо по заданному доверительному интервалу (его полуширине) · По условию задачи определить · По известному значению или · Вычислить степень свободы k=n-1. · Определить доверительную вероятность (или уровень значимости) по таблице Стьюдента, остановившись на равном или ближайшем меньшем значении tp,k в таблице на строке k. Значение доверительной вероятности Р или уровня значимости
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.01 с.) |

 х=σ
х=σ )=2Ф(
)=2Ф( )=2Ф(1)=2·0,3413=0,6826.
)=2Ф(1)=2·0,3413=0,6826. )=2Ф(
)=2Ф( )= 2Ф(2)=2·0,4772=0,9544
)= 2Ф(2)=2·0,4772=0,9544 )=2Ф(
)=2Ф( )= 2Ф(3)=2·0,49865=0,9973
)= 2Ф(3)=2·0,49865=0,9973 ), так и на очень большую изменчивость (при
), так и на очень большую изменчивость (при  ). Для сравнения изменчивости признаков в таких случаях лучше применять коэффициент вариации, равный процентному отношению стандартного отклонения к средней арифметической величине, то есть коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах:
). Для сравнения изменчивости признаков в таких случаях лучше применять коэффициент вариации, равный процентному отношению стандартного отклонения к средней арифметической величине, то есть коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах:
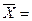 10 мм, а второй (метод Линсенмайера) - σ =15 минут и
10 мм, а второй (метод Линсенмайера) - σ =15 минут и 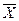 = 180 минут.
= 180 минут.


 ) сведены в таблицу, которая носит название таблица Стьюдента. Из таблицы видно, что при уменьшении числа опытов, но при одной и той же доверительной вероятности, параметр t растет, что объясняется необходимостью расширения интервала, для того чтобы он накрыл неизвестное значение случайной величины. С другой стороны, при одном и том же числе опытов n, но увеличении вероятности того, что интервал накроет значение случайной величины, он должен быть также расширен, поэтому значения t также возрастают.
) сведены в таблицу, которая носит название таблица Стьюдента. Из таблицы видно, что при уменьшении числа опытов, но при одной и той же доверительной вероятности, параметр t растет, что объясняется необходимостью расширения интервала, для того чтобы он накрыл неизвестное значение случайной величины. С другой стороны, при одном и том же числе опытов n, но увеличении вероятности того, что интервал накроет значение случайной величины, он должен быть также расширен, поэтому значения t также возрастают. .
. или стандартную ошибку
или стандартную ошибку