
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное распределение случайной величины. Числовые характеристики нормального распределения и их точечные оценкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если вид кривой распределения описывается формулой Выборки, строго подчиняющиеся нормальному распределению, на практике, как правило, не встречаются. Часто возникают распределения, хотя и не отвечающие строго нормальному распределению, но имеющие с ним сходство. Такие сходные черты часто обусловлены тем, что крайние значения вариантов, близкие к xmin и xmах, встречаются много реже, чем серединные. На практике при первичной обработке данных почти всегда необходимо выяснить, можно ли реальное распределение считать нормальным и насколько значительно заданное распределение отличается от нормального. Это делается с помощью критериев согласия. Нормальное распределение имеет два признака: 1. Чем дальше от центра, тем ниже опускаются ветви графика, что свидетельствует о снижении вероятности появления случайной величины, при сильном отклонении ее от центрального значения. 2. График симметричен относительно центра, что говорит о равных вероятностях появления значений случайной величины как слева от центра, так и справа от него.
Рис. 1.5
Вспомните формулу Pi=fi∆xi. Если график разбить на неширокие интервалы, в пределах которого плотность вероятности остается почти постоянной величиной, то нетрудно понять, что вероятность равна площади S, P=S! В формулу Гаусса входят две величины, которые являются числовыми характеристиками случайной величины или параметрами случайной величины. От их значения зависит вид графика распределения. Одной из задач математической статистики является нахождение, указание данных параметров случайной величины. Первый параметр, обозначаемый как а, называется математическим ожиданием. Он характеризует центр распределения случайной величины. Для нахождения математического ожидания используется формула
Другой числовой характеристикой случайной величины является дисперсия, обозначаемая буквой D или σ2 (D=σ2). Эта величина отражает меру рассеяния значений случайной величины возле центра распределения. Одни значения случайной величины сильнее отличаются от центра, другие меньше. Чтобы оценить степень отклонения любого значения случайной величины от центра (от математического ожидания), а иначе говоря, оценить среднее отклонение, нужно все отклонения (xi – a) сложить и разделить на число испытаний. Но поскольку для нормального распределения все отклонения равновероятны, то получим нуль, т.к. отклонения слева от центра отрицательны, а справа - положительны.
Рис. 1.6
Чтобы этого не случилось, отклонения приходится возводить в квадрат. Получается следующая формула:
где N - объем генеральной совокупности. Т.о. дисперсия будет иметь размерность случайной величины, но только в квадрате. Чтобы избавиться от этого «неудобства» приходится извлекать корень квадратный из дисперсии. Очевидно, что величина, произведенная от дисперсии, также характеризует разброс или рассеяние значений случайной величины вокруг центра. Корень квадратный из дисперсии называется средним квадратичным отклонением (с.к.о.) или стандартным отклонением и обозначается буквой σ (
Когда параметр σ уменьшается, ордината f(x) кривой растет. Подъём кривой в центральной части компенсируется более резким спадом ее к оси 0х, так что общая площадь остается неизменной и равной единице P=S=1. На Рис. 1.6 приведены графики с одним математическим ожиданием, но разным разбросом. Теоретически случайная величина распределенная по нормальному закону, может принимать любые значения от –∞ до +∞. На самом деле, как видно из графика, плотность вероятности по мере удаления от центра быстро убывает и при х=а±3σ значениями плотности вероятности можно пренебречь (Рис.1.7).
Рис. 1.7 Графики распределения продолжительности жизни мужчин и женщин относятся к нормальному распределению, однако числовые характеристики этих распределений различны, поэтому графики будут отличаться друг от друга (Рис. 1.8). Известно, что средняя продолжительность женщин выше у женщин, поэтому график будет сдвинут левее по числовой оси. Известно также, что среди мужчин по разным причинам (войны, бытовые конфликты, суицид и т.д.) жизнь может оборваться в раннем возрасте, а с другой стороны среди мужчин по сравнению с женщинами встречаются долгожители, намного пережившие средний возраст. Таким образом, разброс будет выше у мужчин, а, значит, их график будет шире, но ниже, поскольку площадь, равная вероятности, должна быть одинаковой и равной единице.
Рис. 1.8
Рис. 1.9 Несоответствие нормальному распределению может быть вызвано не только спецификой варьирования признака, но и качественной неоднородностью выборки. Типичный пример такого рода представлен на Рис. 1.9, где проиллюстрирована изменчивость признака в выборке пациентов разного возраста. На гистограмме хорошо видно, что форма распределения имеет двухвершинный облик. Левая вершина распределения соответствует одной возрастной группе, а правая другой. Таким образом, несовпадение с нормальным распределением, в данном случае, явно обусловлено возрастной изменчивостью анализируемого материала. В этом и подобных случаях первоначальную выборку целесообразнее разбить на качественно более однородные группы. Точечные оценки параметров генеральной совокупности по выборкам Если имеются данные обо всех объектах генеральной совокупности, мы можем точно рассчитать значения среднего, дисперсии и стандартного отклонения. На самом деле обследовать все объекты совокупности удается редко. Обычно довольствуются изучением выборки, полагая, что эта выборка отражает свойства совокупности. Имея дело с выборкой, мы, конечно, не узнаем точных значений среднего и стандартного отклонения, но можем оценить их. Оценка среднего для генеральной совокупности (т.е. математического ожидания), вычисленная по выборке, называется выборочным средним арифметическим значением. Выборочное среднее арифметическое значение обозначают
где n – объем выборки. Таким образом Оценка стандартного отклонения называется выборочным стандартным отклонением Sx и определяется следующим образом:
Эта формула отличается от формулы для стандартного отклонения по генеральной совокупности. Во-первых, математическое ожидание а заменяется его выборочной оценкой Выборочное стандартное отклонение в квадрате – это выборочная дисперсия Dx.
Дисперсия выборочная оценивает дисперсию в генеральной совокупности Dx≈D (в литературе эту дисперсию называют исправленная дисперсия).
Выборочное среднее арифметическое значение и выборочное стандартное отклонение есть оценки среднего арифметического значения и стандартного отклонения для генеральной совокупности, вычисленные по случайной выборке. Из одной генеральной совокупности можно взять несколько выборок. Понятно, что разные выборки дадут разные оценки. Для характеристики точности выборочных оценок используют стандартную ошибку. Стандартную ошибку можно подсчитать для любого показателя, но сейчас мы остановимся на стандартной ошибке среднего значения. Она позволяет оценить точность, с которой выборочное среднее характеризует значение среднего по всей генеральной совокупности. Если мы будем исследовать рост 200 студентов и из генеральной совокупности выберем несколько выборок и найдем средний рост в каждой из них, то эти значения, разумеется, будут разными, но не будут слишком сильно отличаться друг от друга. Т.е. их дисперсия будет меньше, чем дисперсия отдельных значений (значений роста отдельных студентов). Можно увидеть, что набор, допустим, из 25 выборочных средних имеет колоколообразное распределение, похожее на нормальное. Поскольку распределение нормальное, его можно описать с помощью среднего значения и стандартного отклонения. Так как среднее значение для рассматриваемых 25 точек есть среднее величин, которые сами являются средними значениями, обозначим его Среднее значение выборочных средних Подобно тому, как стандартное отклонение Sx исходной выборки из 10 студентов служит оценкой изменчивости роста студентов, Распределение выборочных средних приближенно всегда следует нормальному распределению независимо от распределения совокупности, из которой извлечены выборки. В этом состоит суть утверждения, называемого центральной предельной теоремой. Эта теорема гласит следующее.
• Выборочные средние имеют приближенно нормальное распределение независимо от распределения исходной совокупности, из которой были извлечены выборки; • Среднее значение всех возможных выборочных средних равно среднему по генеральной совокупности; • Среднее значение всех возможных средних отклонений по выборкам данного объема, называемое стандартной ошибкой среднего, зависит как от стандартного отклонения генеральной совокупности, так и от объема выборки. Увеличение точности оценки среднего отражается в уменьшении стандартной ошибки среднего Хотя разница между стандартным отклонением и стандартной ошибкой среднего совершенно очевидна, их часто путают. Большинство исследователей приводят в публикациях значение стандартной ошибки среднего, которая заведомо меньше стандартного отклонения. Авторам кажется, что в таком виде их данные внушают больше доверия. Может быть, так оно и есть, однако стандартная ошибка среднего измеряет именно точность оценки среднего, но никак не разброс данных, который зачастую более интересен, чем ошибка среднего. Стандартное же отклонение позволяет судить об изменчивости (вариабельности) изучаемого признака, и помогает врачу сделать заключение об анализах отдельного больного: выходят они за норму или нет. Рассмотрим пример [4], позволяющий почувствовать различие между стандартным отклонением и стандартной ошибкой среднего, а также уяснить, почему не следует пренебрегать стандартным отклонением. Положим, исследователь, обследовав выборку из 20 человек, пишет в статье, что средний сердечный выброс составлял 5,0 л/мин со стандартным отклонением 1 л/мин. Мы знаем, что 95% нормально распределенной совокупности попадает в интервал среднее плюс-минус два стандартных отклонения 2σ. Тем самым, из статьи видно, что почти у всех обследованных сердечный индекс составил от 3 до 7 л/мин. Такие сведения весьма полезны, их легко использовать во врачебной практике. Увы, приведенный пример далек от реальности. Скорее автор укажет не стандартное отклонение, а стандартную ошибку среднего. Тогда из статьи вы узнаете, что «сердечный выброс составил 5,0 ± 0,22 л/мин». И если бы мы спутали стандартную ошибку среднего со стандартным отклонением, то пребывали бы в уверенности, что 95% совокупности заключено в интервал от 4,56 до 5,44 л/мин. На самом деле в этом интервале (с вероятностью 95%) находится среднее значение сердечного выброса. Поэтому очень важно знать, что же именно приводит автор – стандартное отклонение или стандартную ошибку среднего.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1037; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.123.149 (0.012 с.) |

 , то распределение случайной величины называется нормальным. Данную функцию называют функцией плотности вероятности Гаусса. Графиком нормального распределения является колокол симметричный относительно центра распределения.
, то распределение случайной величины называется нормальным. Данную функцию называют функцией плотности вероятности Гаусса. Графиком нормального распределения является колокол симметричный относительно центра распределения.
 , где хi - значения случайной величины – роста, веса и т.д., pi - вероятность появления значения случайной величины. Если учесть, что
, где хi - значения случайной величины – роста, веса и т.д., pi - вероятность появления значения случайной величины. Если учесть, что 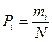 , то получим формулу
, то получим формулу  , из которой видно, что математическое ожидание – это среднее значение случайной величины во всей ее генеральной совокупности. Из графика видно, что при х=а кривая имеет максимум. Т.о. математическое ожидание – это наиболее часто встречаемое значение СВ. Математическое ожидание в медицинских и биологических исследованиях принято называть истинным значением.
, из которой видно, что математическое ожидание – это среднее значение случайной величины во всей ее генеральной совокупности. Из графика видно, что при х=а кривая имеет максимум. Т.о. математическое ожидание – это наиболее часто встречаемое значение СВ. Математическое ожидание в медицинских и биологических исследованиях принято называть истинным значением.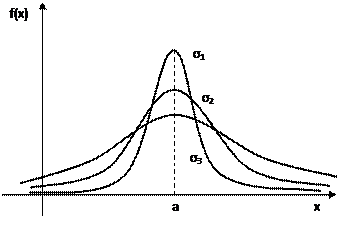
 ,
, ), тогда
), тогда



 и вычисляют по формуле:
и вычисляют по формуле: ,
, . Если значения признака имеют частоты, то используют формулу
. Если значения признака имеют частоты, то используют формулу  .
. .
. .
. или
или  .
. . Аналогично, стандартное отклонение средних обозначим
. Аналогично, стандартное отклонение средних обозначим  ,
,  .
. равно среднему значению всей генеральной совокупности из 200 студентов. Итак, среднее значение выборочных средних совпадет со средним по генеральной совокупности (математическим ожиданием a).
равно среднему значению всей генеральной совокупности из 200 студентов. Итак, среднее значение выборочных средних совпадет со средним по генеральной совокупности (математическим ожиданием a). является оценкой изменчивости значений средних для 25 выборок по 10 студентов в каждой. Таким образом, величина
является оценкой изменчивости значений средних для 25 выборок по 10 студентов в каждой. Таким образом, величина  является оценкой среднего по генеральной совокупности а. Поэтому
является оценкой среднего по генеральной совокупности а. Поэтому  носит название стандартной ошибки среднего. Из последней формулы следует, что, чем больше выборка, тем точнее оценка среднего и тем меньше его стандартная ошибка. Кроме этого, чем больше изменчивость исходной совокупности, тем больше изменчивость выборочных средних, поэтому стандартная ошибка среднего возрастает с увеличением стандартного отклонения совокупности.
носит название стандартной ошибки среднего. Из последней формулы следует, что, чем больше выборка, тем точнее оценка среднего и тем меньше его стандартная ошибка. Кроме этого, чем больше изменчивость исходной совокупности, тем больше изменчивость выборочных средних, поэтому стандартная ошибка среднего возрастает с увеличением стандартного отклонения совокупности. . Набрав достаточное количество студентов, можно сделать стандартную ошибку среднего сколь угодно малой. В отличие от стандартного отклонения стандартная ошибка среднего ничего не говорит о разбросе данных – она лишь показывает точность выборочной оценки среднего.
. Набрав достаточное количество студентов, можно сделать стандартную ошибку среднего сколь угодно малой. В отличие от стандартного отклонения стандартная ошибка среднего ничего не говорит о разбросе данных – она лишь показывает точность выборочной оценки среднего.


