
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непараметрические (свободные от распределения) критерии однородности статистических данныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте СПИСОК ОБОЗНАЧЕНИЙ
μ – математическое ожидание;
α – уровень значимости; N(0,1) – нормальное стандартное распределение;
ВВЕДЕНИЕ Данная курсовая работа посвящена изучению непараметрических критериев однородности статистических данных, которые позволяют проверять различные статистические гипотезы, не зная законов распределения случайных величин. Непараметрический критерий особенно пригоден, когда объем выборки небольшой (настолько, что невозможно было бы оценить закон распределения данных) и данные выражаются в категориальной шкале [5]. Курсовая работа состоит из трех глав. Первая глава посвящена теоретическим основам. В ней рассмотрены существующие непараметрические критерии однородности в статистических данных, их математические модели и применение. Во второй главе, используя данные, полученные из теории, показана реализация непараметрических критериев в статистическом пакете R. Третья глава посвящена исследованиям реализованных критериев. Было проведено исследование распределения статистик рассматриваемых гипотез при "малых" и "больших" выборках. Исследовано распределение статистик по критериям согласия Колмогорова и Смирнова. Была построена эмпирическая функция мощности критериев. Также были собраны реальные данные и проведен анализ данных изученными методами. Реализация критериев и исследования были выполнены при помощи статистического пакета R. Непараметрические критерии сдвига Сравнение параметров сдвига двух совокупностей Быстрый (грубый) критерий Кенуя Пусть Вычисляется среднее значение
со стандартным отклонением
Для очень несимметричных распределений используются оценки
Проверка разности в параметрах положения проверяется критерием
(индексы относятся к номерам проверяемых выборок). При объемах проверяемых выборок свыше 20 статистика критерия распределена нормально. Поэтому нулевая гипотеза отсутствия сдвига не отклоняется при доверительной вероятности α, если Критерий устойчив к отклонениям от нормальности, имеет эффективность по сравнению с параметрическим критерием Стьюдента не хуже ≈93%. Ранговые критерии основываются на последовательности рангов выборочных значений случайных величин. При этом рассматриваются не сами выборочные значения, а их ранги, определяемые порядковым номером элемента выборки в общем ряду, упорядоченном по возрастанию. Например, в упорядоченной выборке Быстрый (грубый) ранговый критерий Рассматриваются две выборки объемов Вычисляем
Поэтому при Эффективность критерия для нормально распределенных выборок 0,95 (для любого другого исходного распределения — не хуже 0,86). Критерий Фишера-Йэйтса-Терри-Гёфдинга Критерий основан на статистике Для
Гипотеза сдвига отклоняется, если статистики Фишера-Йэйтса-Терри-Гёфдинга [1]. Критерий Ван дер Вардена Статистика критерия имеет вид
где Для вычисления квантилей
Гипотеза сдвига отклоняется, если При
Если При Медианный критерий Статистика критерия строится следующим образом. Находится медиана
При
Если
то с достоверностью Иногда применяется другая форма медианного критерия. Пусть А и С — количества элементов выборки
имеющая, при отсутствии сдвига, распределение хи-квадрат с Критерий неприменим, если А, В, С или D < 5 и Критерий Мостеллера Гипотеза равенства средних двух выборок одинакового объема Критерий Розенбаума Применим для двух выборок равного объема. Если не менее 5 (для Критерий рекомендуется использовать для быстрой приближенной проверки гипотезы сдвига [1]. 1.1.2 Сравнение параметров сдвига нескольких ( Критерий Круcкала—Уоллиса Пусть в нашем распоряжении имеются
Упорядочим все Статистика критерия Крускала-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения нескольких сравниваемых выборок имеет вид [1]
где Критерий Крускала-Уоллиса является многомерным обобщением двухвыборочного критерия Вилкоксона-Манна-Уитни. Гипотеза сдвига отклоняется на уровне значимости α, если Аппроксимация Крускала-Уоллиса. Пусть [1]
Тогда статистика [1]
будет иметь при отсутствии сдвига -распределение с
Аппроксимация Имана-Давенпорта. В соответствии с ней нулевая гипотеза сдвига отклоняется с достоверностью α, если [1]
где
Это более точная аппроксимация, чем аппроксимация Крускала-Уоллиса. При наличии связанных рангов (т. е. когда совпадают значения величин из разных выборок и им присваивается одинаковые средние ранги) необходимо использовать модифицированную статистику [1]
где
При Критерий Неменьи Критерий применим для выборок равного объема Гипотеза сдвига считается принятой, если Критерий Вилкоксона—Вилкокс Критерий подобен критерию Неменьи. Пусть имеются
Статистикой критерия является разность
где При Так же, как и критерий Неменьи, настоящий критерий позволяет выявить выборки, приводящие к отклонению нулевой гипотезы [1]. 1.1.2.4. „Быстрый” критерий Кенуя Среди Критерий Ван дер Вардена Статистика Ван дер Вардена для
При справедливости нулевой гипотезы статистика Медианный критерий Для множественного аналога двухвыборочного медианного критерия используется статистика
имеющая при Критерий Хеттманспергера Используется для проверки равенства параметров положения
Нулевая гипотеза отклоняется с достоверностью α, если
где
при Как и в критерии Крускала-Уоллиса, приняты обозначения
и Критерий Ансари—Бредли Является масштабным аналогом критерия Вилкоксона. Сравниваются две выборки
Вычисление статистики критерия может быть выполнено и другим, более простым методом. Поставим элементам упорядоченной по возрастанию выборки
Тогда статистика критерия равна
т. е. она определяется суммой специальным образом назначенных рангов одной выборки. Легко видеть, что при четном (
а при нечетном (
Гипотеза равенства параметров масштаба не отклоняется с достоверностью α, если [1]
где При
где
Нулевая гипотеза равенства параметров масштаба в двух выборках принимается с достоверностью α, если [1]
Эффективность критерия по сравнению с F-критерием в случае нормального распределения равна Критерий Муда Рассмотрен в качестве альтернативы критерию, основанному на F-статистике Фишера, когда вместо наблюдений используются их ранги. Статистика критерия имеет вид [1]
где Нулевая гипотеза равенства параметров масштаба в обеих выборках принимается, если [1]
где При
где
Нулевая гипотеза принимается, если [1]
Эффективность критерия Муда по отношению к F-критерию в случае исходного нормального распределения равна 0,76. Необходимо отметить, что критерий Муда (как и все ранее рассмотренные критерии) предполагает равенство средних (параметров положения). Критерий Сижела-Тьюки Сижел и Тьюки предложили преобразование критериев сдвига в критерии масштаба. Суть их способа сводится к преобразованию первичной упорядоченной объединенной выборки. Пусть
(т. е. оставшийся ряд „переворачивается" каждый раз после приписывания рангов паре крайних значений). Далее проверка гипотезы о разности параметров масштаба в двух выборках аналогична проверке гипотезы сдвига в новой последовательности с описанным правилом нумерации рангов. Если использовать в качестве критерия проверки нулевой гипотезы сумму рангов
Здесь При
Если Критерий Кейпена Является масштабным аналогом критерия Фишера-Йэйтса-Терри-Гёфдинга. Если
где Нулевая гипотеза отклоняется, если
где При
где
При Квартальный критерий Критерий является интуитивным аналогом медианного критерия сдвига. Статистика критерия имеет вид
Название критерия исходит из того, что S приблизительно равно числу наблюдений из первой выборки, лежащих за пределами первой и третьей квартилей объединенной выборки. Точнее, S получается, если подсчитать количество наблюдений При
Поэтому нулевая гипотеза равенства параметров масштаба принимается, если
где α – доверительная вероятность. Эффективность критерия по сравнению с F-критерием в случае нормального распределения невелика и равна ≈ 0,37, поэтому им рекомендуется пользоваться при
Реализация критерия Муда В статистическом пакете R сформируем две выборки по стандартному нормальному закону распределения с объемами выборок Увеличим объем выборок. При Для данных выборок по критерию Муда принимается гипотеза ИССЛЕДОВАНИЯ 3.1. Исследование распределения статистик рассматриваемых гипотез при "малых" и "больших" выборках Рассмотрим критерий Манна-Уитни-Вилкосона. При выполнении гипотезы
Методом Монте-Карло смоделируем выборку, состоящую из статистик Вилкоксона при выполнении гипотезы
Рисунок 3.1 – График теоретической и эмпирической функций распределения статистики Вилкоксона критерия Манна-Уитни-Вилкоксона при объеме смоделированных значений статистик mm=100 и объеме выборок m=25 и n=30, моделируемых по стандартному нормальному закону распределения (α=0,05)
Рисунок 3.2 – График теоретической и эмпирической функций распределения статистики Вилкоксона критерия Манна-Уитни-Вилкоксона при объеме смоделированных значений статистик mm=1000 и объеме выборок m=25 и n=30, моделируемых по стандартному нормальному закону распределения (α=0,05) Из рисунков 3.1 и 3.2 видим, что при увеличении объема выборки эмпирическая функция распределения статистики стремится к ее теоретической функции распределения. Реальные данные 1. Имеются две выборки случайных величин:
Необходимо проверить гипотезу сдвига критериями группы Манна-Уитни-Вилкоксона при доверительной вероятности α=0,95. При реализации данного критерия c заданными выборками в статистическом пакете R получаем, что по статистике Манна-Уитни гипотеза сдвига отклоняется. Ограничим исходную выборку восьмью значениями.
Применив критерий Манна-Уитни-Вилкоксона для полученной выборки получаем, что по статистике Манна-Уитни и по ранговой статистике Вилкоксона гипотеза сдвига отклоняется. 2. Перед началом игры двум группам детей дошкольного возраста показали два мультипликационных фильма. Одна группа (условие А) просмотрела фильм, содержание которого было с ярко выраженными агрессивными элементами; второй группе (условие В) был показан фильм без каких-либо агрессивных элементов. После просмотра фильмов каждый ребенок некоторое время играл отдельно от своих товарищей, причем опытные наблюдатели зарегистрировали количество поступков агрессивного характера, совершенных ребенком по отношению к его игрушкам в течение этого периода. Отметкой для каждого ребенка в данном случае является общее число совершенных им подобных поступков, которые, однако, различаются по характеру и по силе. Поэтому исследователи сочли более правильным рассматривать эти отметки только как относительную меру агрессивности (порядковая шкала). Полученные результаты были следующими [4]: Условие А: 26,22,19,21,14,18,29,17,11,34; Условие В: 16,10,8,13,19,11,7,13,9,21;
Проверить какая гипотеза выполняется с помощью критерия Манна-Уитни-Вилкоксона. Воспользовавшись реализацией данного критерия в статистическом пакете R, получили следующие результаты: по статистике Манна-Уитни и по ранговой статистике Вилкоксона принимается гипотеза 3. Чтобы установить, отличаются ли механизмы фатальной соевой астмы от механизмов обычной фатальной астмы, число CD3+ Т-клеток в подслизистой основе, показателе иммунной системы организма, сравнили с числом клеток в 7 случаях фатальной соевой астмы и в 10 случаях фатальной астмы. Из-за маленьких размеров выборки и явно скошенных (асимметричных) данных используем двухвыборочный критерий Манна-Уитни-Вилкоксона [5]. Соевая астма: 0,00; 0,00; 0,00; 1,36; 1,43; 4,01; 34,45. Фатальная астма: 3,76; 4,32; 13,75; 37,50; 58,33; 73,63; 74,17; 99,99; 154,86; 1225,51. Рассматриваются гипотезы:
Используем критерий Манна-Уитни-Вилкоксона для данных выборок и получаем, что механизмы фатальной соевой астмы отличаются от механизмов обычной фатальной астмы (принимается гипотеза 4. В результате наблюдений получены пять выборок случайных величин (k = 5)
Необходимо проверить гипотезу об отсутствии сдвига между параметрами положения в выборках критерием Крускала-Уоллиса на уровне значимости α=0,05 [1]. Используя реализацию данного критерия в статистическом пакете R получаем следующий результат: по аппроксимации Крускала-Уоллиса и по аппроксимации Имана-Давенпорта гипотеза сдвига принимается. 5. Имеются две выборки случайных величин:
Проверить гипотезу равенства параметров масштаба в выборках критерием Ансари-Бредли при достоверности α=0,95 [1]. При проверке получаем, что гипотеза равенства параметров масштаба принимается. 6. Даны две выборки случайных величин:
Поверить гипотезу равенства параметров масштаба критерием Муда при достоверности α=0,95 [1]. Применив критерий Муда к данным выборкам, получаем, что гипотеза равенства параметров масштаба принимается. 7. 95 призванных на военную службу мужчин в возрасте 16-20 лет прошли осмотр зубов, когда зачислялись в Королевские вооруженные силы. Их зубы были осмотрены через год после лечения. У человека 28 зубов кроме зубов мудрости, и в этом исследовании каждый зуб имел 4 интересующие дантистов точки; каждый участник имел минимум 84 и максимум 112 измеряемых точек. Изучали влияние лечения на глубину десневого кармана (большая глубина кармана означает ухудшение состояния зуба). Данные показывают процент измеряемых сайтов, для которых была утрата прикрепления при каждой оценке в каждом из 14 этих участников. Утрата прикрепления — показатель заболевания десен, которое может
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.014 с.) |

 – основная гипотеза;
– основная гипотеза; – альтернативная гипотеза;
– альтернативная гипотеза; – элемент выборки
– элемент выборки  ;
;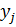 – элемент выборки
– элемент выборки  ;
; - ранги элементов выборки;
- ранги элементов выборки; – cредний ранг;
– cредний ранг; – дисперсия;
– дисперсия; – эмпирическая функция распределения;
– эмпирическая функция распределения; – теоретическая функция распределения.
– теоретическая функция распределения.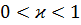 . Через
. Через  обозначим такое значение случайной величины, которое превышается
обозначим такое значение случайной величины, которое превышается  значениями из выборки.
значениями из выборки.
 , где
, где  .
. ;
; 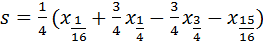 .
. ,
, .
. выборочное значение
выборочное значение 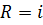 .
. и
и  при
при  (
( ). Их элементы ранжируются по возрастанию совместно. Одинаковым наблюдениям присваивается одинаковый усредненный ранг. Для каждой группы находятся суммы рангов
). Их элементы ранжируются по возрастанию совместно. Одинаковым наблюдениям присваивается одинаковый усредненный ранг. Для каждой группы находятся суммы рангов  и
и  и средние ранги
и средние ранги  и
и  .
. . Статистика -критерия может быть аппроксимирована нормальным распределением со средним
. Статистика -критерия может быть аппроксимирована нормальным распределением со средним  и дисперсией
и дисперсией .
. гипотеза сдвига отклоняется с доверительной вероятностью α.
гипотеза сдвига отклоняется с доверительной вероятностью α. - математическое ожидание -ой порядковой статистики в выборке объема
- математическое ожидание -ой порядковой статистики в выборке объема  из стандартного нормального распределения;
из стандартного нормального распределения;  - ранг значений
- ранг значений  в объединенной ранжированной выборке
в объединенной ранжированной выборке  в объединенной выборке, тогда суммирование нужно вести по
в объединенной выборке, тогда суммирование нужно вести по 
 может быть использована аппроксимация
может быть использована аппроксимация , где
, где 
 , где
, где  - критические значения
- критические значения
 – γ - квантиль стандартного нормального распределения.
– γ - квантиль стандартного нормального распределения. может быть применено приближение
может быть применено приближение .
. , где
, где  - критические значения статистики Ван дер Вардена.
- критические значения статистики Ван дер Вардена.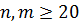 распределение X удовлетворительно описывается нормальным со средним
распределение X удовлетворительно описывается нормальным со средним  и дисперсией
и дисперсией
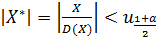 , гипотеза сдвига отклоняется с достоверностью α.
, гипотеза сдвига отклоняется с достоверностью α. эффективность критерия Ван дер Вардена не уступает эффективности критерия Стьюдента [1].
эффективность критерия Ван дер Вардена не уступает эффективности критерия Стьюдента [1]. общего упорядоченного ряда
общего упорядоченного ряда 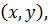 и подсчитывается число наблюдений выборки
и подсчитывается число наблюдений выборки  нечетно и медиана принадлежит выборке
нечетно и медиана принадлежит выборке  , где
, где 
 распределение
распределение  удовлетворительно описывается нормальным со средним
удовлетворительно описывается нормальным со средним 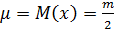 и дисперсией
и дисперсией

 гипотеза сдвига отклоняется.
гипотеза сдвига отклоняется.
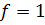 степенью свободы.
степенью свободы. . Эффективность медианного критерия по сравнению с критерием Стьюдента в случае нормального распределения равна 2/π ≈ 0,64 [1].
. Эффективность медианного критерия по сравнению с критерием Стьюдента в случае нормального распределения равна 2/π ≈ 0,64 [1].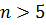 отклоняется с доверительной вероятностью 0,95, если 5 (при
отклоняется с доверительной вероятностью 0,95, если 5 (при 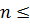 25) или 6 (при
25) или 6 (при  ) наибольших или наименьших значений содержатся в одной и той же выборке. Критерий имеет низкую мощность и может быть рекомендован только для быстрой грубой проверки гипотез сдвига [1].
) наибольших или наименьших значений содержатся в одной и той же выборке. Критерий имеет низкую мощность и может быть рекомендован только для быстрой грубой проверки гипотез сдвига [1]. и α=0,95) или 7 (для
и α=0,95) или 7 (для  и α = 0,99) значений одной выборки находятся вне размаха второй выборки, то нулевая гипотеза отсутствия сдвига на указанных уровнях достоверности отклоняется.
и α = 0,99) значений одной выборки находятся вне размаха второй выборки, то нулевая гипотеза отсутствия сдвига на указанных уровнях достоверности отклоняется. ) совокупностей
) совокупностей выборок случайных величин
выборок случайных величин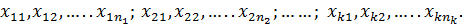
 элементов выборок по возрастанию и обозначим через
элементов выборок по возрастанию и обозначим через  ранг
ранг  -ого элемента
-ого элемента  -й выборки в общем упорядоченном ряду.
-й выборки в общем упорядоченном ряду.
 . (1.17)
. (1.17) , где
, где  - критическое значение критерия Крускала-Уоллиса для
- критическое значение критерия Крускала-Уоллиса для  . При
. При  применимы различные аппроксимации.
применимы различные аппроксимации. (1.18)
(1.18) (1.19)
(1.19)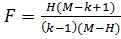 (1.20)
(1.20) и
и  степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью α, если [1]
степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью α, если [1] (
( ). (1.21)
). (1.21) (1.22)
(1.22) (1.23)
(1.23) - соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы.
- соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы. , (1.24)
, (1.24) (1.25)
(1.25) – размер
– размер  группы одинаковых элементов; q – количество одинаковых элементов.
группы одинаковых элементов; q – количество одинаковых элементов. 20 справедлива аппроксимация распределения статистики
20 справедлива аппроксимация распределения статистики 
 -распределением с
-распределением с  степенями свободы, т. е. нулевая гипотеза отклоняется, если
степенями свободы, т. е. нулевая гипотеза отклоняется, если 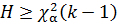 .
. ). Статистика критерия, предложенного Неменьи, в обозначениях, принятых для критерия Крускала-Уоллиса имеет вид
). Статистика критерия, предложенного Неменьи, в обозначениях, принятых для критерия Крускала-Уоллиса имеет вид 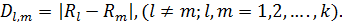
 , где
, где  – критические значения критерия Неменьи [1].
– критические значения критерия Неменьи [1]. –
– 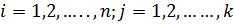 ). Обозначим через
). Обозначим через  и через
и через  сумму рангов -й выборки.
сумму рангов -й выборки.

 (α) - критические значения критерия Вилкоксона-Вилкокс.
(α) - критические значения критерия Вилкоксона-Вилкокс. (α) с доверительной вероятностью α гипотеза сдвига принимается.
(α) с доверительной вероятностью α гипотеза сдвига принимается. и наименьшее среди наибольших значений
и наименьшее среди наибольших значений  в выборках. Подсчитываются количества
в выборках. Подсчитываются количества  наблюдений, для которых
наблюдений, для которых 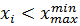 и
и 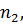 для которых
для которых  . Статистикой критерия Кенуя является сумма
. Статистикой критерия Кенуя является сумма  .
.  – критические значения критерия Кенуя [1].
– критические значения критерия Кенуя [1]. выборок имеет вид
выборок имеет вид .
. распределена как
распределена как  , где
, где 
 (>10) распределение хи-квадрат c
(>10) распределение хи-квадрат c 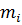 – число наблюдений -й выборки, превосходящих медиану объединенной выборки (
– число наблюдений -й выборки, превосходящих медиану объединенной выборки ( ) [1].
) [1]. против альтернатив упорядоченности
против альтернатив упорядоченности  где хотя бы одно из неравенств — строгое. Статистика критерия
где хотя бы одно из неравенств — строгое. Статистика критерия
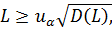
 – α-квантиль стандартного нормального распределения,
– α-квантиль стандартного нормального распределения,
 .
.
 ) в общем упорядоченном по возрастанию ряду. Статистикой критерия Ансари—Бредли является [1]
) в общем упорядоченном по возрастанию ряду. Статистикой критерия Ансари—Бредли является [1] (1.26)
(1.26)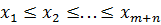 объема
объема  в соответствие ранги по следующему правилу
в соответствие ранги по следующему правилу
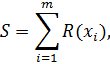
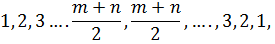

 , (1.27)
, (1.27) - критические значения статистики Ансари-Бредли.
- критические значения статистики Ансари-Бредли. можно использовать асимптотическую нормальность распределения величины [1]
можно использовать асимптотическую нормальность распределения величины [1] (1.28)
(1.28) (1.29)
(1.29) (1.30)
(1.30) (1.31)
(1.31)
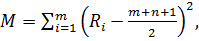 (1.32)
(1.32) в общем упорядоченном ряду значений
в общем упорядоченном ряду значений  (
( ).
). , (1.33)
, (1.33) и
и  - критические значения статистики Муда.
- критические значения статистики Муда. справедлива нормальная аппроксимация [1]
справедлива нормальная аппроксимация [1] (1.34)
(1.34) (1.35)
(1.35) (1.36)
(1.36) (1.37)
(1.37) — первичная объединенная выборка. Из нее получаем новую последовательность вида
— первичная объединенная выборка. Из нее получаем новую последовательность вида
 элементов выборки меньшего объема в такой последовательности, то нулевая гипотеза принимается, если
элементов выборки меньшего объема в такой последовательности, то нулевая гипотеза принимается, если  , где
, где  и
и  - критические значения которые могут быть получены с помощью критических значений критерия Манна-Уитни. Для этого необходимо найти
- критические значения которые могут быть получены с помощью критических значений критерия Манна-Уитни. Для этого необходимо найти  и
и  из таблицы критических значений критерия Манна-Уитни для заданных α,
из таблицы критических значений критерия Манна-Уитни для заданных α,  и затем вычислить
и затем вычислить

 , нулевая гипотеза равенства параметров масштаба принимается с достоверностью α [1].
, нулевая гипотеза равенства параметров масштаба принимается с достоверностью α [1]. в общем упорядоченном ряду (
в общем упорядоченном ряду (
 - математическое ожидание квадрата -й порядковой статистики в выборке объема (
- математическое ожидание квадрата -й порядковой статистики в выборке объема (
 и
и  - критические значения статистики Кейпена.
- критические значения статистики Кейпена.

 нулевая гипотеза принимается с достоверностью α.
нулевая гипотеза принимается с достоверностью α.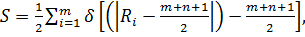 где
где  , для которых
, для которых  или
или  , и, если
, и, если 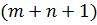 делится на 4, прибавить 1/2 в случае, когда
делится на 4, прибавить 1/2 в случае, когда  или
или  для некоторого
для некоторого  , или прибавить 1 в случае, когда оба последних равенства имеют место для некоторых двух различных индексов
, или прибавить 1 в случае, когда оба последних равенства имеют место для некоторых двух различных индексов 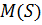 и дисперсией
и дисперсией  , где
, где

 > 50 [1].
> 50 [1]. и
и 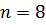 . Упорядочим по возрастанию объединенную выборку. По формуле (1.32) вычислим статистику критерия. Найдем по таблице критических значений статистики Муда при заданных объемах выборок
. Упорядочим по возрастанию объединенную выборку. По формуле (1.32) вычислим статистику критерия. Найдем по таблице критических значений статистики Муда при заданных объемах выборок 
 Нулевая гипотеза равенства параметров масштаба в выборках принимается, если выполняется условие (1.33).
Нулевая гипотеза равенства параметров масштаба в выборках принимается, если выполняется условие (1.33).
 статистика Вилкоксона W имеет стандартное нормальное распределение
статистика Вилкоксона W имеет стандартное нормальное распределение  , функция распределения которого имеет вид [7]
, функция распределения которого имеет вид [7] (3.1)
(3.1)




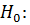 не существует различия между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов.
не существует различия между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов. существует различие между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов.
существует различие между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов.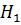 .
.








