
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий Фишера-Терри-Йэйтса-ГёфдингаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вариант критерия Фишера-Терри-Йэйтса-Гёфдинга для
где При Критерий Ван дер Вардена Статистика Ван дер Вардена для
При справедливости нулевой гипотезы статистика Медианный критерий Для множественного аналога двухвыборочного медианного критерия используется статистика
имеющая при Критерий Хеттманспергера Используется для проверки равенства параметров положения
Нулевая гипотеза отклоняется с достоверностью α, если
где
при Как и в критерии Крускала-Уоллиса, приняты обозначения
и Непараметрические критерии масштаба Непараметрические ранговые критерии сравнения параметров масштаба строятся на базе соответствующих критериев сдвига изменением либо статистики критерия, либо правил присвоения рангов наблюдениям. Критерии масштаба преследуют цель выявить возможные различия в мерах разброса (изменчивости) наблюдений в двух или более выборках. Сравнение параметров масштаба двух совокупностей Критерий Ансари—Бредли Является масштабным аналогом критерия Вилкоксона. Сравниваются две выборки
Вычисление статистики критерия может быть выполнено и другим, более простым методом. Поставим элементам упорядоченной по возрастанию выборки
Тогда статистика критерия равна
т. е. она определяется суммой специальным образом назначенных рангов одной выборки. Легко видеть, что при четном (
а при нечетном (
Гипотеза равенства параметров масштаба не отклоняется с достоверностью α, если [1]
где При
где
Нулевая гипотеза равенства параметров масштаба в двух выборках принимается с достоверностью α, если [1]
Эффективность критерия по сравнению с F-критерием в случае нормального распределения равна Критерий Муда Рассмотрен в качестве альтернативы критерию, основанному на F-статистике Фишера, когда вместо наблюдений используются их ранги. Статистика критерия имеет вид [1]
где Нулевая гипотеза равенства параметров масштаба в обеих выборках принимается, если [1]
где При
где
Нулевая гипотеза принимается, если [1]
Эффективность критерия Муда по отношению к F-критерию в случае исходного нормального распределения равна 0,76. Необходимо отметить, что критерий Муда (как и все ранее рассмотренные критерии) предполагает равенство средних (параметров положения). Критерий Сижела-Тьюки Сижел и Тьюки предложили преобразование критериев сдвига в критерии масштаба. Суть их способа сводится к преобразованию первичной упорядоченной объединенной выборки. Пусть
(т. е. оставшийся ряд „переворачивается" каждый раз после приписывания рангов паре крайних значений). Далее проверка гипотезы о разности параметров масштаба в двух выборках аналогична проверке гипотезы сдвига в новой последовательности с описанным правилом нумерации рангов. Если использовать в качестве критерия проверки нулевой гипотезы сумму рангов
Здесь При
Если Критерий Кейпена Является масштабным аналогом критерия Фишера-Йэйтса-Терри-Гёфдинга. Если
где Нулевая гипотеза отклоняется, если
где При
где
При Квартальный критерий Критерий является интуитивным аналогом медианного критерия сдвига. Статистика критерия имеет вид
Название критерия исходит из того, что S приблизительно равно числу наблюдений из первой выборки, лежащих за пределами первой и третьей квартилей объединенной выборки. Точнее, S получается, если подсчитать количество наблюдений При
Поэтому нулевая гипотеза равенства параметров масштаба принимается, если
где α – доверительная вероятность. Эффективность критерия по сравнению с F-критерием в случае нормального распределения невелика и равна ≈ 0,37, поэтому им рекомендуется пользоваться при
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.241.118 (0.01 с.) |

 выборок основан на статистике
выборок основан на статистике
 - ранг элементов -й выборки в общем ряду (
- ранг элементов -й выборки в общем ряду ( ).
). распределение статистики
распределение статистики  может быть аппроксимировано
может быть аппроксимировано  -распределением с
-распределением с  степенями свободы. Поэтому нулевая гипотеза отсутствия сдвига отклоняется с достоверностью
степенями свободы. Поэтому нулевая гипотеза отсутствия сдвига отклоняется с достоверностью  , если
, если 
 .
. распределена как
распределена как  , где
, где 
 (>10) распределение хи-квадрат c
(>10) распределение хи-квадрат c 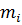 – число наблюдений -й выборки, превосходящих медиану объединенной выборки (
– число наблюдений -й выборки, превосходящих медиану объединенной выборки ( ) [1].
) [1]. против альтернатив упорядоченности
против альтернатив упорядоченности  где хотя бы одно из неравенств — строгое. Статистика критерия
где хотя бы одно из неравенств — строгое. Статистика критерия
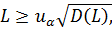
 – α-квантиль стандартного нормального распределения,
– α-квантиль стандартного нормального распределения,
 .
.
 -ого элемента
-ого элемента  -й выборки в общем упорядоченном ряду [1].
-й выборки в общем упорядоченном ряду [1]. и
и 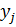 объемами
объемами  и
и  соответственно. Пусть
соответственно. Пусть  - ранги элементов одной из выборок (предположим,
- ранги элементов одной из выборок (предположим,  ) в общем упорядоченном по возрастанию ряду. Статистикой критерия Ансари—Бредли является [1]
) в общем упорядоченном по возрастанию ряду. Статистикой критерия Ансари—Бредли является [1] (1.26)
(1.26)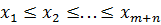 объема
объема  в соответствие ранги по следующему правилу
в соответствие ранги по следующему правилу
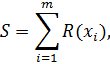
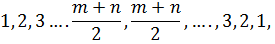

 , (1.27)
, (1.27) - критические значения статистики Ансари-Бредли.
- критические значения статистики Ансари-Бредли. можно использовать асимптотическую нормальность распределения величины [1]
можно использовать асимптотическую нормальность распределения величины [1] (1.28)
(1.28) (1.29)
(1.29) (1.30)
(1.30) (1.31)
(1.31)
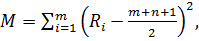 (1.32)
(1.32) в общем упорядоченном ряду значений
в общем упорядоченном ряду значений  (
( ).
). , (1.33)
, (1.33) и
и  - критические значения статистики Муда.
- критические значения статистики Муда. справедлива нормальная аппроксимация [1]
справедлива нормальная аппроксимация [1] (1.34)
(1.34) (1.35)
(1.35) (1.36)
(1.36) (1.37)
(1.37) — первичная объединенная выборка. Из нее получаем новую последовательность вида
— первичная объединенная выборка. Из нее получаем новую последовательность вида
 элементов выборки меньшего объема в такой последовательности, то нулевая гипотеза принимается, если
элементов выборки меньшего объема в такой последовательности, то нулевая гипотеза принимается, если  , где
, где  и
и  - критические значения которые могут быть получены с помощью критических значений критерия Манна-Уитни. Для этого необходимо найти
- критические значения которые могут быть получены с помощью критических значений критерия Манна-Уитни. Для этого необходимо найти  и
и  из таблицы критических значений критерия Манна-Уитни для заданных α,
из таблицы критических значений критерия Манна-Уитни для заданных α,  и затем вычислить
и затем вычислить

 , нулевая гипотеза равенства параметров масштаба принимается с достоверностью α [1].
, нулевая гипотеза равенства параметров масштаба принимается с достоверностью α [1]. в общем упорядоченном ряду (
в общем упорядоченном ряду (
 - математическое ожидание квадрата -й порядковой статистики в выборке объема (
- математическое ожидание квадрата -й порядковой статистики в выборке объема (
 и
и  - критические значения статистики Кейпена.
- критические значения статистики Кейпена.

 нулевая гипотеза принимается с достоверностью α.
нулевая гипотеза принимается с достоверностью α.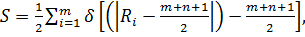 где
где 
 , для которых
, для которых  или
или  , и, если
, и, если 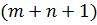 делится на 4, прибавить 1/2 в случае, когда
делится на 4, прибавить 1/2 в случае, когда  или
или  для некоторого
для некоторого  , или прибавить 1 в случае, когда оба последних равенства имеют место для некоторых двух различных индексов
, или прибавить 1 в случае, когда оба последних равенства имеют место для некоторых двух различных индексов 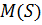 и дисперсией
и дисперсией  , где
, где


 > 50 [1].
> 50 [1].


