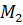Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эмпирическая мощность критериевСодержание книги Поиск на нашем сайте
Рассмотрим критерий Крускала-Уоллиса. При использовании аппроксимации Крускала-Уоллиса получаем статистику F, которая при выполнении нулевой гипотезы имеет распределение Фишера с Мощность критерия – вероятность принятия альтернативной гипотезы при условии, что она верна. Построим график зависимости
Рисунок 3.8 – График зависимости эмпирической функции мощности критерия Крускала-Уоллиса от объема моделируемой статистики фиксированных объемах моделируемых выборок, которые имеют нормальное распределение с параметрами
С увеличением объема моделируемой статистики вероятность ошибки стремится к нулю, а мощность возрастает и стремится к единице. Реальные данные 1. Имеются две выборки случайных величин:
Необходимо проверить гипотезу сдвига критериями группы Манна-Уитни-Вилкоксона при доверительной вероятности α=0,95. При реализации данного критерия c заданными выборками в статистическом пакете R получаем, что по статистике Манна-Уитни гипотеза сдвига отклоняется. Ограничим исходную выборку восьмью значениями.
Применив критерий Манна-Уитни-Вилкоксона для полученной выборки получаем, что по статистике Манна-Уитни и по ранговой статистике Вилкоксона гипотеза сдвига отклоняется. 2. Перед началом игры двум группам детей дошкольного возраста показали два мультипликационных фильма. Одна группа (условие А) просмотрела фильм, содержание которого было с ярко выраженными агрессивными элементами; второй группе (условие В) был показан фильм без каких-либо агрессивных элементов. После просмотра фильмов каждый ребенок некоторое время играл отдельно от своих товарищей, причем опытные наблюдатели зарегистрировали количество поступков агрессивного характера, совершенных ребенком по отношению к его игрушкам в течение этого периода. Отметкой для каждого ребенка в данном случае является общее число совершенных им подобных поступков, которые, однако, различаются по характеру и по силе. Поэтому исследователи сочли более правильным рассматривать эти отметки только как относительную меру агрессивности (порядковая шкала). Полученные результаты были следующими [4]: Условие А: 26,22,19,21,14,18,29,17,11,34; Условие В: 16,10,8,13,19,11,7,13,9,21;
Проверить какая гипотеза выполняется с помощью критерия Манна-Уитни-Вилкоксона. Воспользовавшись реализацией данного критерия в статистическом пакете R, получили следующие результаты: по статистике Манна-Уитни и по ранговой статистике Вилкоксона принимается гипотеза 3. Чтобы установить, отличаются ли механизмы фатальной соевой астмы от механизмов обычной фатальной астмы, число CD3+ Т-клеток в подслизистой основе, показателе иммунной системы организма, сравнили с числом клеток в 7 случаях фатальной соевой астмы и в 10 случаях фатальной астмы. Из-за маленьких размеров выборки и явно скошенных (асимметричных) данных используем двухвыборочный критерий Манна-Уитни-Вилкоксона [5]. Соевая астма: 0,00; 0,00; 0,00; 1,36; 1,43; 4,01; 34,45. Фатальная астма: 3,76; 4,32; 13,75; 37,50; 58,33; 73,63; 74,17; 99,99; 154,86; 1225,51. Рассматриваются гипотезы:
Используем критерий Манна-Уитни-Вилкоксона для данных выборок и получаем, что механизмы фатальной соевой астмы отличаются от механизмов обычной фатальной астмы (принимается гипотеза 4. В результате наблюдений получены пять выборок случайных величин (k = 5)
Необходимо проверить гипотезу об отсутствии сдвига между параметрами положения в выборках критерием Крускала-Уоллиса на уровне значимости α=0,05 [1]. Используя реализацию данного критерия в статистическом пакете R получаем следующий результат: по аппроксимации Крускала-Уоллиса и по аппроксимации Имана-Давенпорта гипотеза сдвига принимается. 5. Имеются две выборки случайных величин:
Проверить гипотезу равенства параметров масштаба в выборках критерием Ансари-Бредли при достоверности α=0,95 [1]. При проверке получаем, что гипотеза равенства параметров масштаба принимается. 6. Даны две выборки случайных величин:
Поверить гипотезу равенства параметров масштаба критерием Муда при достоверности α=0,95 [1]. Применив критерий Муда к данным выборкам, получаем, что гипотеза равенства параметров масштаба принимается. 7. 95 призванных на военную службу мужчин в возрасте 16-20 лет прошли осмотр зубов, когда зачислялись в Королевские вооруженные силы. Их зубы были осмотрены через год после лечения. У человека 28 зубов кроме зубов мудрости, и в этом исследовании каждый зуб имел 4 интересующие дантистов точки; каждый участник имел минимум 84 и максимум 112 измеряемых точек. Изучали влияние лечения на глубину десневого кармана (большая глубина кармана означает ухудшение состояния зуба). Данные показывают процент измеряемых сайтов, для которых была утрата прикрепления при каждой оценке в каждом из 14 этих участников. Утрата прикрепления — показатель заболевания десен, которое может быть более запущенным, чем определяется по глубине десневого кармана. Использовали критерий знаковых рангов Вилкоксона, чтобы исследовать, влияло ли лечение на утрату прикрепления.
Рассматриваются следующие гипотезы:
До лечения (%): 65,5; 75,0; 87,2; 97,1; 100,0; 92,6; 82,3; 90,0; 93,0; 100,0; 91,7; 97,7; 79,0; 95,4; После лечения (%): 100,0; 10,0; 100,0; 97,1; 99,1; 100,0; 91,6; 94,6; 95,5; 97,3; 92,3; 98,0; 100,0; 99,0. По ранговой статистике Вилкоксона принимаем гипотезу 8. При измерении частоты пульса через 2 минуты окончания физической нагрузки у 10 спортсменов (выборка
Проверить гипотезу сдвига критериями группы Манна-Уитни-Вилкоксона при доверительной вероятности α=0,95. Получаем результаты: по статистике Манна-Уитни гипотеза сдвига отклоняется; по ранговой статистике Вилкоксона гипотеза сдвига принимается. 9. Имеется экспериментальная группа, состоящая из 25 человек (N = 25), и контрольная группа, состоящая из 30 человек (M = 30), и измерение заключается в определении числа хондроцитов в 1 мкм ткани регенерата на седьмые сутки после травмы. В дальнейшем число хондроцитов будет обозначено как степень регенерации суставного хряща (СРСХ). Экспериментальным воздействием в рассматриваемом примере выступала стимуляция заживления (регенерации), в то время как в контрольной группе имела место естественная регенерация. Результаты измерений СРСХ в контрольной и экспериментальной группах до и после эксперимента: Контрольная группа до начала эксперимента: 15,13,11,18,10,8,20,7,8,12,15,16,13,14,14,19,7,8,11,12,15,16,13,5,11,19,18,9,6,15. Экспериментальная группа до начала эксперимента: 12,11,15,17,18,6,8,10,16,12,15,14,19,13,19,12,11,16,12,8,13,7,15,8,9. Контрольная группа после окончания эксперимента: 16,12,14,17,11,9,15,8,6,13,17,19,15,11,9,19,8,6,9,12,11,17,10,8,8,20,19,6,14,10. Экспериментальная группа после окончания эксперимента: 15,18,12,20,16,11,13,7,14,17,19,16,12,15,19,18,14,13,18,13,13,15,18,9,14. C помощью критерия Манна-Уитни-Вилкоксона проверить гипотезу о равенстве сравниваемых выборок [10]. Для этого сравним сначала оценки СРСХ в контрольной и экспериментальной группе до начала эксперимента. Гипотеза о том, что сравниваемые выборки совпадают, принимается на уровне значимости 0,05. Теперь сравним оценки СРСХ в контрольной и экспериментальной группе после окончания эксперимента. Достоверность различий сравниваемых выборок составляет 95%. Итак, начальные (до начала эксперимента) состояния экспериментальной и контрольной групп совпадают, а конечные (после окончания эксперимента) – различаются. Следовательно, можно сделать вывод, что эффект изменений обусловлен именно применением экспериментального воздействия.
ЗАКЛЮЧЕНИЕ При выполнении курсовой работы были изучены непараметрические критерии однородности статистических данных. Разработана программа, в которой представлены математические модели методов проверки гипотез, реализованные в статистическом пакете R. В результате проведения исследований данных критериев было показано, что с увеличением объема моделируемых статистик эмпирическая функция распределения рассматриваемых статистик стремится к теоретической функции распределения. При исследовании распределения статистик по критериям согласия Колмогорова и Смирнова получили, что с увеличением объема количества смоделированных статистик вероятность ошибки уменьшается. При исследовании асимптотических свойств было выявлено, что с увеличением объема моделируемых статистик математическое ожидание стремится к теоретическому значению. Были собраны реальные данные из области медицины и проведен их анализ при помощи реализованных критериев.
Литература: 1. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. - М.: ФИЗМАТЛИТ, 2006. - 816 с. 2. Харин Ю. С., Степанова М. Д. Практикум на ЭВМ по математической статистике. – Мн.: Изд-во «Университетское», 1987. – 304 с. 3. Айвазян С.А., Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное изд. / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. — 471с. 4. Рунион Р. Справочник по непараметрической статистике: Современный подход / Пер. с англ. Е. 3. Демиденко; Предисл. Ю. Н. Тюрина. – М.: Финансы и статистика, 1982. – 198с. 5. Петри А., Сэбин К. Наглядная статистика в медицине. – М.: ГЭОТАР-МЕД, 2003. – 143c. 6. Малета Ю. С., Тарасов В. В. Непараметрические методы статистического анализа в биологии и медицине. – М.: Изд-во Моск. ун-та, 1982. – 178с. 7. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям / Пер. с англ. А. К. Звонкина. – М.:Статистика,1980. – 95с. 8. Методические указания к лабораторным работам по курсу «Методы анализа данных»/ Меретилов М.А. - Красноярск: КГТУ, 2006. - 15 с. 9. Буховец А. Г., Москалев П. В., Богатова В. П., Бирючинская Т. Я. Статистический анализ данных в системе R. Учебное пособие – Воронеж: ВГАУ, 2010. – 124с. 10. Новиков Д. А., Новочадов В. В. Статистические методы в медико-биологическом эксперименте (типовые случаи). – Волгоград: Изд-во ВолГМУ, 2005. – 84с.
Приложение А. Критические значения статистик непараметрических критериев Таблица А.1 − Критические значения (
Продолжение таблицы А.1
Окончание таблицы А.1
Таблица А.2 − Критические значения (
Таблица А.3−Критические значения (
Приложение Б ТЕКСТ ПРОГРАММЫ Листинг Б.1 Реализация критерия Манна-Уитни-Вилкоксона и его исследование в программе GNU R MUV<-function(x,y) {x<-sort(x);y<-sort(y); n<-length(x);m<-length(y); H<-0;t<-0;t1<-0;t2<-0; a<-c();b1<-c(); b2<-c(); b<-c(); razn<-c();otsR<-c(); for (i in (1:n)) for (j in (1:m)) if (x[i]<y[j]) {H<-H+1}; U<-U1U2(n,m); if ((H>U[1]) && (H<U[2])) {cat("по статистике Манна-Уитни гипотеза сдвига отклоняется", "\n")} else {cat("по статистике Манна-Уитни гипотеза сдвига принимается", "\n")}; if (m!=n) {R<-m*n+n*(n+1)/2-H; for (i in (1:n)) #в a совпадающие значения, в t их количество for (j in (1:m)) if ((x[i]==y[j]) && (x[i]!=x[i+1]) && (y[j]!=y[j+1])) { t<-t+1; a[t]<-x[i];}; ch<-R-n*(n+m+1)/2; if ((n>20) && (m>20) && (t==0)) {zn<-(n*m*(n+m+1)/12)^0.5; #если повторяющихся чисел нет W<-ch/zn;}; if (t!=0) {for (l in (1:t)) {for (i in (1:n)) if (x[i]==a[l]) {t1<-t1+1; b1[l]<-t1;} t1<-0;}; for (l in (1:t)) {for (j in (1:m)) if (y[j]==a[l]) {t2<-t2+1; b2[l]<-t2;} t2<-0;}; s<-0; for (l in (1:t)) {b[l]<-b1[l]+b2[l]; # в b количество каждого повторяющегося элемента s<-s+b[l]*((b[l])^2-1);}} if ((n>20) && (m>20) && (t!=0)) {s1<-1-s/((m+n)*(m+n-1)*(m+n+1)); zn<-((n*m*(n+m+1)/12)*s1)^0.5; #повторяющиеся числа есть W<-ch/zn; }
if ((n>20) && (m>20)) {if (abs(W)<qnorm(0.975)) {cat("по статистике Вилкоксона гипотеза сдвига отклоняется", "\n")} #статистика Вилкоксона else {cat("по статистике Вилкоксона гипотеза сдвига принимается", "\n")}} if ((n>20) && (m>20)){ I<-W/2*(1+((n+m-2)/(n+m-1-W^2))^0.5); #аппроксимация Имана I1<-1/(2*qnorm(0.975))+1/(2*qt(0.975,n+m-2)); if (abs(I)<=I1) {cat("по аппроксимации Имана гипотеза сдвига отклоняется", "\n")} else {cat("по аппроксимации Имана гипотеза сдвига принимается", "\n")};};};
if (n==m) #ранговый критерий Вилкоксона {for (i in (1:n)) razn[i]<-abs(x[i]-y[i]); otsR<-sort(razn); for (i in (1:n)) if (otsR[i]>0) {TV<-i; break;}; TV1<-T1T2(n); if ((TV>=TV1[1]) && (TV<=TV1[2])) {cat("по ранговой статистике Вилкоксона гипотеза сдвига отклоняется", "\n")} else {cat("по ранговой статистике Вилкоксона гипотеза сдвига принимается", "\n")} if (n>=20) {TVm<-(TV-n*(n+1)/4)/(n*(n+1)*(2*n+1))^0.5; #приближение if (abs(TVm)<qnorm(0.975)) {cat("по приближению гипотеза сдвига отклоняется", "\n")} else {G5<-cat("по приближению гипотеза сдвига принимается", "\n")}; K<-TVm/2*(1+((n-1)/(n-TVm^2))^0.5); #более точное приближение K1<-1/(2*qnorm(0.975))+1/(2*(qt(0.975,n-1))); if (abs(K)<K1) {G6<-cat("по более точному приближению гипотеза сдвига отклоняется", "\n")} else {G6<-cat("по более точному приближению гипотеза сдвига принимается", "\n")};} } return(H); }
ginit<-function(xmin,xmax,ymin,ymax,xl="",yl="") #построение координатных осей {plot(c(xmin,xmax),c(ymin,ymax),type="n",xlab=xl,ylab=yl);}; #моделирование методом Монте-Карло mm<-1000; SMUV<-rep(NA,mm); S<-rep(NA,mm); for (i in 1:mm) {ksi<-rnorm(22); eta<-rnorm(25); HH<-MUV(ksi,eta); SMUV[i]<-HH;} for (i in 1:mm) #для статистики W {if (abs(SMUV[i])<qnorm(0.975)){S[i]<-SMUV[i]}}
DrawFE<-function(color="black")#построение эмпирической функции распределения {ksi1<-sort(S); k1<-0; {for(i in 1:length(ksi1)) {k<-k1+1/length(ksi1); lines(c(ksi1[i],ksi1[i+1]),c(k,k),col=color); points(ksi1[i],k,col=color); k1<-k; }; }; }; #для статистики W DrawFT<-function(h=0.01,color="red")#построение теоретической функции распределения {S<-sort(S); X<-min(S); while (X<=max(S)) {lines(c(X,X+h),c(pnorm(X),pnorm(X)),col=color); X=X+h; }; }; X11(); ginit(min(sort(S)),max(sort(S)),0,1,xl="W",yl="F(W)"); DrawFE(); DrawFT(); fDn<-function(SMUV) #статистика D в критерии согласия Колмогорова {ksi3<-sort(SMUV); a1<-max(c(abs(1/length(ksi3)-pnorm(ksi3[1])), abs(0/length(ksi3)-pnorm(ksi3[1])))); for(i in 2:length(ksi3)) {a1<-max(c(a1,abs(i/length(ksi3)-pnorm(ksi3[i])), abs((i-1)/length(ksi3)-pnorm(ksi3[i])))); }; return(a1); }; fnWn2<-function(SMUV) #статистика W в критерии согласия Смирнова-Крамера-Мизеса {ksi3<-sort(SMUV); n<-length(ksi3); s1<-0 for(i in 1:n) {s1<-s1+(pnorm(ksi3[i])-(2*i-1)/(2*n))^2 }; return(1/(12*n)+(1)*s1); }; Dn<-fDn(SMUV); Dn; deltaD<-1.36; if ((((length(SMUV))^(1/2))*Dn)<deltaD) {HD<-0;} else {HD<-1;}; nWn2<-fnWn2(SMUV); nWn2; deltaW<-0.461; if (nWn2<deltaW) {HW<-0;} else {HW<-1;}; HD; HW; X11(); n<-1000; ginit(0,n,0,1,"n","Dn"); ksi2<-rnorm(1); fDn2<-fDn(ksi2); for (i in 2:n) {fDn1<-fDn2; ksi2<-rnorm(i); fDn2<-fDn(ksi2); lines(c(i-1,i),c(fDn1,fDn2),col="black"); }; X11(); ginit(0,n,0,2,"n","sqrt(n)*Dn"); ksi2<-rnorm(1); fDn2<-fDn(ksi2); for (i in 2:n) {fDn1<-fDn2; ksi2<-rnorm(i); fDn2<-fDn(ksi2); lines(c(i-1,i),c(((i-1)^(1/2))*fDn1,(i^(1/2))*fDn2),col="black"); }; X11(); ginit(0,n,0,1,"n","nW"); ksi2<-rnorm(1); fWn2<-fnWn2(ksi2); for (i in 3:n) {fWn1<-fWn2; ksi2<-rnorm(i); fWn2<-fnWn2(ksi2); lines(c(i-1,i),c(fWn1,fWn2),col="black"); }; X11(); ginit(0,n,0,1,"n","W"); ksi2<-rnorm(1); fWn2<-fnWn2(ksi2); for (i in 2:n) {fWn1<-fWn2; ksi2<-rnorm(i); fWn2<-fnWn2(ksi2); lines(c(i-1,i),c(fWn1/(i-1),fWn2/i),col="black"); }; Dn; nWn2; tMO<-0; tMO; tD<-1; tD; n<-1000; #выборочная оценка параметра, мат ожидание gama<-0.95; X11(); eps<-(tD/(1*(1-gama)))^(1/2); ginit(0,n,tMO-eps/2,tMO+eps/2,"n","M"); lines(c(0,n),c(tMO,tMO),col="red"); ksi2<-rnorm(1); for (i in 2:n) {ksi3<-ksi2; ksi2<-rnorm(i); lines(c(i-1,i),c(mean(ksi3),mean(ksi2)),col="blue"); }; for (i in 2:n) {eps1<-(tD/((i-1)*(1-gama)))^(1/2); eps2<-(tD/((i)*(1-gama)))^(1/2); lines(c(i-1,i),c(tMO+eps1,tMO+eps2),col="red"); lines(c(i-1,i),c(tMO-eps1,tMO-eps2),col="red"); }; Листинг Б.2 Реализация критерия Крускала-Уоллиса в программе GNU R KU<-function(x1,x2,x3,x4,x5) {k<-5; kl<-c();kv<-c();kk<-c();kv1<-c();res<-c(); n1<-length(x1); n2<-length(x2); n3<-length(x3); n4<-length(x4); n5<-length(x5); N<-n1+n2+n3+n4+n5; X<-c(x1,x2,x3,x4,x5); X<-sort(X); q1<-1; for (i in 1:length(X)) {q<-X[i]; for (j in 1:length(X)) if ((j!=i) && (X[j]==q)) { q1<-q1+1;} kl[i]<-q1; q1<-1;} Matr<-matrix(X,length(X),1); Matr<-cbind(Matr,c(kl)); jj<-0; for (i in 1:length(X)) {qq<-X[i]; for (j in 1:length(X)) if (kl[i]!=1) {if (X[j]==qq) {jj<-jj+j;} kk[i]<-jj/kl[i]} else kk[i]<-i; jj<-0; } Matr<-cbind(Matr,c(kk)); R1<-0; for (i in 1:n1) for (j in 1:length(X)) {if (x1[i]==X[j]) {R1<-R1+Matr[j,3]; break;}; } R11<-R1/n1; R2<-0; for (i in 1:n2) for (j in 1:length(X)) {if (x2[i]==X[j]) {R2<-R2+Matr[j,3]; break;}; } R22<-R2/n2; R3<-0; for (i in 1:n3) for (j in 1:length(X)) {if (x3[i]==X[j]) {R3<-R3+Matr[j,3]; break;}; } R33<-R3/n3; R4<-0; for (i in 1:n4) for (j in 1:length(X)) {if (x4[i]==X[j]) {R4<-R4+Matr[j,3]; break;}; } R44<-R4/n4; R5<-0; for (i in 1:n5) for (j in 1:length(X)) {if (x5[i]==X[j]) {R5<-R5+Matr[j,3]; break;}; } R55<-R5/n5; HH<-12/(N*(N+1))*((R1^2)/n1+(R2^2)/n2+(R3^2)/n3+(R4^2)/n4+(R5^2)/n5)-3*(N+1); M<-(N^3-(n1^3+n2^3+n3^3+n4^3+n5^3))/(N*(N+1)); V<-2*(k-1)-2*(3*(k^2)-6*k+N*(2*(k^2)-6*k+1))/(5*N*(N+1))-6/5*(1/n1+1/n2+1/n3+1/n4+1/n5); v1<-((k-1)*((k-1)*(M-k+1)-V))/(0.5*M*V); v2<-(M-k+1)*v1/(k-1); F<-(HH*(M-k+1))/((k-1)*(M-HH)); v<-1; for (i in (1:N)) if (Matr[i,2]!=1) {kv[v]<-Matr[i,1]; v<-v+1} qf<-qf(0.95,v1,v2); if (F<qf) {cat("по аппроксимации Крускала-Уоллиса гипотеза сдвига отклоняется","\n")} else {cat("по аппроксимации Крускала-Уоллиса гипотеза сдвига принимается","\n")} ############аппроксимация Имана-Давенпорта J<-(HH/2)*(1+(N-k)/(N-1-HH)); J1<-0.5*((k-1)*qf(0.95,k-1,N-k)+qchisq(0.95,4)); if (J>=J1) {cat("по аппроксимации Имана-Давенпорта гипотеза сдвига принимается","\n")} else {cat("по аппроксимации Имана-Давенпорта гипотеза сдвига отклоняется","\n")} res<-c(F,v1,v2); return(res); } #моделирование методом Монте-Карло mm<-500; SKU<-rep(NA,mm); S1<-rep(NA,mm); FF<-c(); vv1<-c(); vv2<-c(); for (i in 1:mm) {ksi1<-rnorm(8); ksi2<-rnorm(10); ksi3<-rnorm(12); ksi4<-rnorm(14); ksi5<-rnorm(16); FF<-KU(ksi1,ksi2,ksi3,ksi4,ksi5); SKU[i]<-FF[1]; vv1[i]<-FF[2]; vv2[i]<-FF[3]; } ########################мощность критерия k<-5; m1<-70; D1<-rep(NA,m1); n1<-k+1; kol<-0; Wn<-c(); ni<-c(); for (j in 1:(400-k)) {for (i in (1:m1)) {ksi1<-rnorm(n1,25,sqrt(150)); ksi2<-rnorm(n1,30,sqrt(150)); ksi3<-rnorm(n1,35,sqrt(150)); ksi4<-rnorm(n1,40,sqrt(150)); ksi5<-rnorm(n1,45,sqrt(150)); D<-KU(ksi1,ksi2,ksi3,ksi4,ksi5); D1[i]<-D[1]; if (D1[i]>qf(0.975,vv1[1],vv2[1])) {kol<-kol+1}} Wn[j]<-kol/m1; ni[j]<-n1; n1<-n1+1; kol<-0;} Wn ni X11() plot(ni,Wn,"l",col="black"); Листинг Б.3 Реализация критерия Ансари-Бредли в программе GNU R AB<-function(x,y) {R1<-c(); R2<-c(); X1<-c(); m<-length(x); n<-length(y); X<-c(x,y); X<-sort(X); N<-length(X); Matr<-matrix(X,N,1); Matr<-cbind(Matr,(1:N)); сhet<-c(); k<-1; for (i in (1:N)) {l<-Matr[i,1]; for (j in (1:m)) if (l==x[j]) {R1[k]<-Matr[i,2]; k<-k+1};} k<-1; for (i in (1:N)) {l<-Matr[i,1]; for (j in (1:n)) if (l==y[j]) {R2[k]<-Matr[i,2]; k<-k+1};} s1<-(m+n+1)/2; S<-0; for (i in (1:m)) S<-S+(s1-abs(R1[i]-s1)); Ss<-S1S2(m,n); if ((S>Ss[1]) && (S<Ss[2])) {cat("Гипотеза равенства параметров масштаба принимается","\n")} else {cat("Гипотеза равенства параметров масштаба отклоняется","\n")} chet<-c(18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50); for (i in 1:(length(chet))) if ((m+n)==chet[i]) {Ch<-1}; if (Ch==1) {M<-(m*(m+n+2))/4} else {M<-(m*(m+n+1)^2)/(4*(m+n))} if (Ch==1) {D<-(m*n*(m+n-2)*(m+n+2))/(48*(n+m-1))} else {D<-(m*n*(m+n+1)*((m+n)^2+3))/(48*(m+n)^2)} SA<-(S-M)/sqrt(D); if (SA<qnorm(0.975)) {cat("по аппроксимации гипотеза равенства параметров масштаба принимается","\n")} else {cat("по аппроксимации гипотеза равенства параметров масштаба отклоняется","\n")} return(SA)} Листинг Б.4 Реализация критерия Муда в программе GNU R M<-function(x1,x2) {Rx1<-c(); m<-length(x1); n<-length(x2); X<-c(x1,x2); X<-sort(X); N<-n+m; Matr<-matrix(X,N) Matr<-cbind(Matr,(1:N));
for (i in (1:N)) {c<-Matr[i,1]; for (j in (1:m)) if (x1[j]==c) {Rx1[j]<-Matr[i,2]};}
SM<-0; m1<-(m+n+1)/2; for (i in (1:m)) SM<-SM+(Rx1[i]-m1)^2;
SMs<-M1M2(m,n); if ((SM>SMs[1]) && (SM<SMs[2])) {cat("гипотеза о равенстве параметров масштаба принимается","\n")} else {cat("гипотеза о равенстве параметров масштаба отклоняется","\n")}
MM<-(m*(m+n+1)*(m+n-1))/12; D<-(m*n*(m+n+1)*(m+n+2)*(m+n-2))/180; M1<-(SM-MM+0.5)/(sqrt(D)); if (abs(M1)<qnorm(0.975)) {cat(" по аппроксимации гипотеза о равенстве параметров масштаба принимается","\n")} else {cat("по аппроксимации гипотеза о равенстве параметров масштаба отклоняется","\n")}
return(M1); }
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.203.255 (0.011 с.) |

 и
и  степенями свободы (
степенями свободы ( от n, где
от n, где  – количество неправильно принимаемых гипотез в m=70 испытаниях и фиксированных объемах моделируемой статистики n.
– количество неправильно принимаемых гипотез в m=70 испытаниях и фиксированных объемах моделируемой статистики n.
 при
при
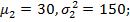
 ;
; ;
;  . (α=0,05)
. (α=0,05)


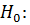 не существует различия между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов.
не существует различия между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов. существует различие между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов.
существует различие между медианами для отметок об агрессивности детей после просмотра мультипликационных фильмов.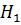 .
.





 ) и у 10 лиц, не занимающихся спортом (выборка
) и у 10 лиц, не занимающихся спортом (выборка  ), получены следующие данные (ударов в 1 минуту) [6]:
), получены следующие данные (ударов в 1 минуту) [6]:

 статистики Манна-Уитни
статистики Манна-Уитни - доверительная вероятность)
- доверительная вероятность)


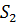
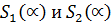 статистики Ансари-Бредли
статистики Ансари-Бредли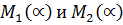 статистики Муда
статистики Муда