
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий Манна-Уитни-ВилкоксонаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Пусть
Здесь
Если
гипотеза сдвига отклоняется ( С -статистикой Манна-Уитни связана статистика Вилкоксона, определяемая суммой рангов элементов одной выборки (предположим,
При
Статистика W аппроксимируется нормальным распределением, и гипотеза сдвига отклоняется с достоверностью
Если в двух сравниваемых выборках есть совпадающие значения, то им рекомендуется приписывать средние ранги (среднеарифметическое для каждой серии последовательных рангов). При этом в знаменателе статистики следует использовать величину [1]
где Более точная аппроксимация предложена Иманом [1]. В соответствии с ней гипотеза сдвига отклоняется с достоверностью
где
Асимптотическая эффективность критерия Манна—Уитни равна Одним из вариантов применения рассмотренного критерия является так называемый ранговый критерий Вилкоксона. Его статистика строится следующим образом. Для двух выборок
который затем ранжируется по возрастанию. В упорядоченном ряду значений
Гипотеза сдвига отклоняется, если [1]
где При
При [1]
гипотеза сдвига отклоняется (здесь Гипотеза сдвига отклоняется на уровне достоверности
где
Критерий Фишера-Йэйтса-Терри-Гёфдинга Критерий основан на статистике Для
Гипотеза сдвига отклоняется, если статистики Фишера-Йэйтса-Терри-Гёфдинга [1]. Критерий Ван дер Вардена Статистика критерия имеет вид
где Для вычисления квантилей
Гипотеза сдвига отклоняется, если При
Если При Медианный критерий Статистика критерия строится следующим образом. Находится медиана
При
Если
то с достоверностью Иногда применяется другая форма медианного критерия. Пусть А и С — количества элементов выборки
имеющая, при отсутствии сдвига, распределение хи-квадрат с Критерий неприменим, если А, В, С или D < 5 и Критерий Мостеллера Гипотеза равенства средних двух выборок одинакового объема Критерий Розенбаума Применим для двух выборок равного объема. Если не менее 5 (для Критерий рекомендуется использовать для быстрой приближенной проверки гипотезы сдвига [1]. 1.1.2 Сравнение параметров сдвига нескольких ( Критерий Круcкала—Уоллиса Пусть в нашем распоряжении имеются
Упорядочим все Статистика критерия Крускала-Уоллиса для проверки гипотезы о наличии сдвига в параметрах положения нескольких сравниваемых выборок имеет вид [1]
где Критерий Крускала-Уоллиса является многомерным обобщением двухвыборочного критерия Вилкоксона-Манна-Уитни. Гипотеза сдвига отклоняется на уровне значимости α, если Аппроксимация Крускала-Уоллиса. Пусть [1]
Тогда статистика [1]
будет иметь при отсутствии сдвига -распределение с
Аппроксимация Имана-Давенпорта. В соответствии с ней нулевая гипотеза сдвига отклоняется с достоверностью α, если [1]
где
Это более точная аппроксимация, чем аппроксимация Крускала-Уоллиса. При наличии связанных рангов (т. е. когда совпадают значения величин из разных выборок и им присваивается одинаковые средние ранги) необходимо использовать модифицированную статистику [1]
где
При Критерий Неменьи Критерий применим для выборок равного объема Гипотеза сдвига считается принятой, если Критерий Вилкоксона—Вилкокс Критерий подобен критерию Неменьи. Пусть имеются
Статистикой критерия является разность
где При Так же, как и критерий Неменьи, настоящий критерий позволяет выявить выборки, приводящие к отклонению нулевой гипотезы [1]. 1.1.2.4. „Быстрый” критерий Кенуя Среди
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 964; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

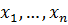 и
и  - упорядоченные по возрастанию выборки. Для проверки гипотезы сдвига Манн и Уитни предложили ранговый критерий, основанный на статистике [1]
- упорядоченные по возрастанию выборки. Для проверки гипотезы сдвига Манн и Уитни предложили ранговый критерий, основанный на статистике [1] , где
, где  =
= 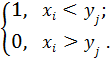 (1.1)
(1.1) - точное число пар значений
- точное число пар значений  и
и 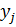 , для которых
, для которых  .
.
 (1.2)
(1.2) - критические значения критерия Манна-Уитни) [1].
- критические значения критерия Манна-Уитни) [1]. ) в общей упорядоченной последовательности элементов совместной выборки объема (
) в общей упорядоченной последовательности элементов совместной выборки объема ( ) [1]:
) [1]: (1.3)
(1.3) применима аппроксимация [1]
применима аппроксимация [1] (1.4)
(1.4) , если
, если (1.5)
(1.5) (1.6)
(1.6) — общее число групп совпадающих величин;
— общее число групп совпадающих величин;  - число совпавших величин в i-й группе (следует помнить, что совпадения учитываются только тогда, когда совпавшие величины принадлежат различным выборкам, т. е. совпадения, целиком состоящие из элементов одной и той же выборки, на величину W не влияют).
- число совпавших величин в i-й группе (следует помнить, что совпадения учитываются только тогда, когда совпавшие величины принадлежат различным выборкам, т. е. совпадения, целиком состоящие из элементов одной и той же выборки, на величину W не влияют). , если
, если (1.7)
(1.7)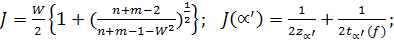 (1.8)
(1.8) -
-  -
-  степенями свободы;
степенями свободы;  .
.
 и
и  одинакового объема
одинакового объема 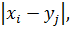 (1.9)
(1.9) находится сумма рангов Т величин [1]
находится сумма рангов Т величин [1] . (1.10)
. (1.10)
 , (1.11)
, (1.11) - критические значения статистики Т знакового рангового критерия Вилкоксона.
- критические значения статистики Т знакового рангового критерия Вилкоксона. применимо приближение [1]
применимо приближение [1] (1.12)
(1.12) (1.13)
(1.13) –
–  -квантиль стандартного нормального распределения).
-квантиль стандартного нормального распределения). если [1]
если [1] (1.14),
(1.14), (1.15)
(1.15) –
–  - квантиль стандартного нормального распределения;
- квантиль стандартного нормального распределения;  -
-  степенями свободы.
степенями свободы. - математическое ожидание -ой порядковой статистики в выборке объема
- математическое ожидание -ой порядковой статистики в выборке объема  из стандартного нормального распределения;
из стандартного нормального распределения;  - ранг значений
- ранг значений  в объединенной ранжированной выборке
в объединенной ранжированной выборке  и
и  в объединенной выборке, тогда суммирование нужно вести по
в объединенной выборке, тогда суммирование нужно вести по 
 может быть использована аппроксимация
может быть использована аппроксимация , где
, где 
 , где
, где  - критические значения
- критические значения
 может быть применено приближение
может быть применено приближение .
. , где
, где  - критические значения статистики Ван дер Вардена.
- критические значения статистики Ван дер Вардена.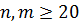 распределение X удовлетворительно описывается нормальным со средним
распределение X удовлетворительно описывается нормальным со средним  и дисперсией
и дисперсией
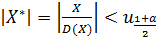 , гипотеза сдвига отклоняется с достоверностью α.
, гипотеза сдвига отклоняется с достоверностью α. эффективность критерия Ван дер Вардена не уступает эффективности критерия Стьюдента [1].
эффективность критерия Ван дер Вардена не уступает эффективности критерия Стьюдента [1]. общего упорядоченного ряда
общего упорядоченного ряда 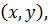 и подсчитывается число наблюдений выборки
и подсчитывается число наблюдений выборки  нечетно и медиана принадлежит выборке
нечетно и медиана принадлежит выборке  , где
, где 
 распределение
распределение  удовлетворительно описывается нормальным со средним
удовлетворительно описывается нормальным со средним 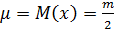 и дисперсией
и дисперсией

 гипотеза сдвига отклоняется.
гипотеза сдвига отклоняется.
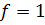 степенью свободы.
степенью свободы. . Эффективность медианного критерия по сравнению с критерием Стьюдента в случае нормального распределения равна 2/π ≈ 0,64 [1].
. Эффективность медианного критерия по сравнению с критерием Стьюдента в случае нормального распределения равна 2/π ≈ 0,64 [1].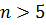 отклоняется с доверительной вероятностью 0,95, если 5 (при
отклоняется с доверительной вероятностью 0,95, если 5 (при 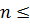 25) или 6 (при
25) или 6 (при  ) наибольших или наименьших значений содержатся в одной и той же выборке. Критерий имеет низкую мощность и может быть рекомендован только для быстрой грубой проверки гипотез сдвига [1].
) наибольших или наименьших значений содержатся в одной и той же выборке. Критерий имеет низкую мощность и может быть рекомендован только для быстрой грубой проверки гипотез сдвига [1]. и α=0,95) или 7 (для
и α=0,95) или 7 (для  ) совокупностей
) совокупностей выборок случайных величин
выборок случайных величин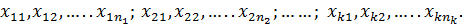
 элементов выборок по возрастанию и обозначим через
элементов выборок по возрастанию и обозначим через  ранг
ранг  -ого элемента
-ого элемента  -й выборки в общем упорядоченном ряду.
-й выборки в общем упорядоченном ряду.
 . (1.17)
. (1.17) , где
, где  - критическое значение критерия Крускала-Уоллиса для
- критическое значение критерия Крускала-Уоллиса для  . При
. При  применимы различные аппроксимации.
применимы различные аппроксимации. (1.18)
(1.18) (1.19)
(1.19)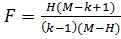 (1.20)
(1.20) и
и  степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью α, если [1]
степенями свободы. Таким образом, нулевая гипотеза отклоняется с достоверностью α, если [1] (
( ). (1.21)
). (1.21) (1.22)
(1.22) (1.23)
(1.23) - соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы.
- соответственно критические значения статистик Фишера и хи-квадрат с соответствующими степенями свободы. , (1.24)
, (1.24) (1.25)
(1.25) – размер
– размер  группы одинаковых элементов; q – количество одинаковых элементов.
группы одинаковых элементов; q – количество одинаковых элементов. 20 справедлива аппроксимация распределения статистики
20 справедлива аппроксимация распределения статистики 
 -распределением с
-распределением с  степенями свободы, т. е. нулевая гипотеза отклоняется, если
степенями свободы, т. е. нулевая гипотеза отклоняется, если 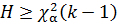 .
. ). Статистика критерия, предложенного Неменьи, в обозначениях, принятых для критерия Крускала-Уоллиса имеет вид
). Статистика критерия, предложенного Неменьи, в обозначениях, принятых для критерия Крускала-Уоллиса имеет вид 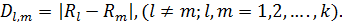
 , где
, где  – критические значения критерия Неменьи [1].
– критические значения критерия Неменьи [1]. –
– 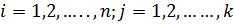 ). Обозначим через
). Обозначим через  и через
и через  сумму рангов -й выборки.
сумму рангов -й выборки.

 (α) - критические значения критерия Вилкоксона-Вилкокс.
(α) - критические значения критерия Вилкоксона-Вилкокс. (α) с доверительной вероятностью α гипотеза сдвига принимается.
(α) с доверительной вероятностью α гипотеза сдвига принимается. и наименьшее среди наибольших значений
и наименьшее среди наибольших значений  в выборках. Подсчитываются количества
в выборках. Подсчитываются количества  наблюдений, для которых
наблюдений, для которых 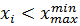 и
и 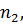 для которых
для которых  . Статистикой критерия Кенуя является сумма
. Статистикой критерия Кенуя является сумма  .
.  – критические значения критерия Кенуя [1].
– критические значения критерия Кенуя [1].


