
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка статистичних гіпотез. Критерій Колмогорова, Колмогорова-Смірнова.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1)Гіпотези про розподіл
Головна гіпотеза Альтернатив. 2)Гіпотези однорідності
3)Гіпотези незалежності
Критерій згоди-апарат перевірки гіпотез
При справедлив.
Критерій Колмогорова для перевірки гіпотез про розподіл
Якщо, справедливе
Якщо, Для непер. Критерій Колмогорова-Смірнова
Задача про вибір двох простих гіпотез. Лема Неймана-Пірсона. Нехай Лема Неймана-Пірсона. Серед усіх можливих критичний областей, для яких ймовірність похибки першого роду дорівнює Доведення.
Критерій Неймана-Пірсона для перевірки простих гіпотез про математичне сподівання для нормального розподілу.
Теорема.
Доведення:
Критерій Неймана-Пірсона для дискретних розподілів. Рандомізовані критерії.
З ймов.
Якщо
Нехай функція
Перевірка гіпотез про рівність математичних сподівань двох нормальних сукупностей Нехай маємо
1.
2.
Перевірка гіпотез про рівність дисперсій двох вибірок з нормальних сукупностей. 3.
Фішера-Снедекора:
4.
Послідовний аналіз. Критерій Вальда.
Якщо
Припустимо, що
Теорема 1. Теорема 2. Конст.
Критерій
Критерій Вальда
Елементи кореляційного аналізу. Коефіцієнт тісноти зв’язку
Для лінійн. ф-цій вик.
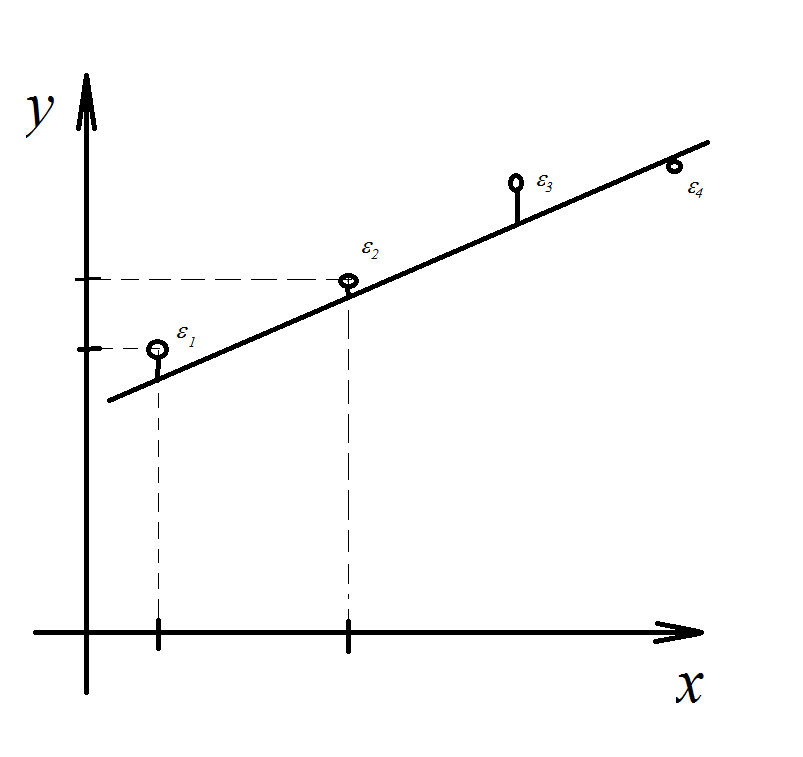
Метод найменших квадратів. Лінійна регресія.
МНК (Гаус)
Лінійна регресія:
Коефіцієнти кореляції рангів Спірмена та Кендела. n умовних спостережень над 2 вип. вел
Приклад:
Чисуттєвийзв’язок?
Коефіцієнт кореляції рангів Кендела: Якщо є однакові ранги знаходимо середнє арифметичне t – кількість повторів
Приклад:
Однофакторний дисперсійний аналіз. Дисперсійний аналіз – це статматаналіз статспостереж., які залежать від різнодночасно діючихфакт. Вибір найважл ф та оцінка їх впливу. Спостереження Перевіряємо
Q=Q1+Q2 – тотожність однофакторного дисперсійного аналізу. Q1 – сер.- квадратичне відхилення по факт. А Q2 - залишкове відхилення.
Критерій перевірки гіпотези.
Двофакторний дисперсійний аналіз.
Де дисперсія більша, той фактор сильніше впливає.
Статистичні рішаючи функції. Байєсівське та мінімаксне рішення. Байєсівськерішення
Прав.
Мінімаксне рішення
Оцінки параметрів та перевірки гіпотез з позиції теорії рішень.
Задача класифікації спостережень.
Вводимо множину класифікації: Втрати: Середні втрати: Вектор втрат: Байсівське рішення Апріорний розподіл: Усереднення по зростанню: Апостеріорний розпод: Середні втрати по апостеріорному розподілу:
Розглянемо 2 частинні випадки: 1) Нехай
Принцип максимуму апостеріорної ймовірності:
2) Нехай k=2
Класифікація спостережень у випадку двох нормальних сукупностей.
фі(х) – дискримінантна лінійна функція
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.14.48 (0.009 с.) |

 ,
, 
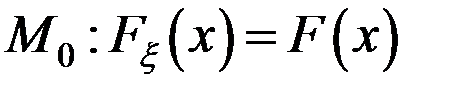
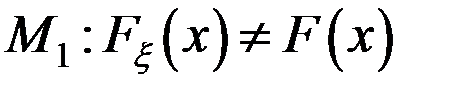
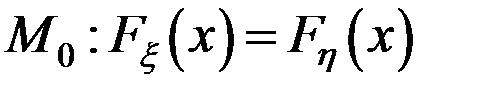

 - незалежні
- незалежні - залежні
- залежні - критерій
- критерій можна порахувати. Шукається порогове
можна порахувати. Шукається порогове  .
.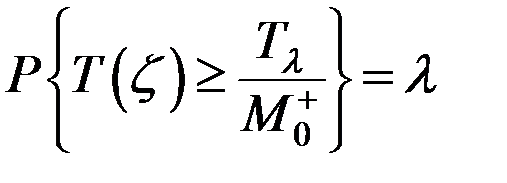
 ;
; 
 ,
, 



 , то
, то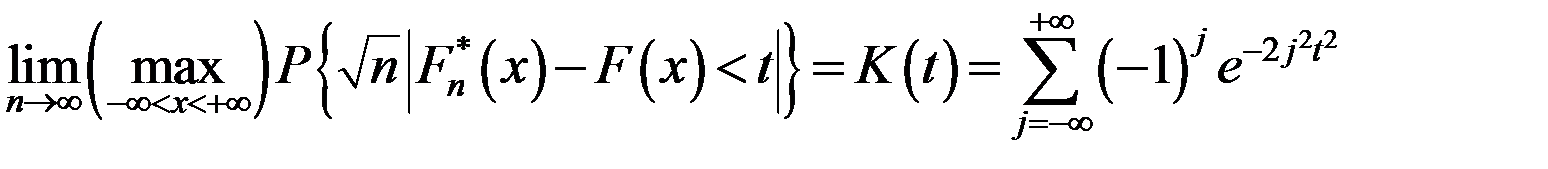

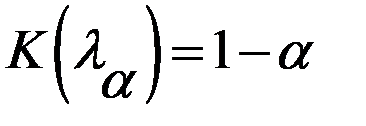


 де
де  - емпіричні ф-ії розподілу, побудовані за першою і другою вибірками. При
- емпіричні ф-ії розподілу, побудовані за першою і другою вибірками. При  розподіл випадкової величини
розподіл випадкової величини  збігається до розподілу Колмогорова. Якщо,
збігається до розподілу Колмогорова. Якщо,  , то гіпотеза
, то гіпотеза  відхиляється, а при
відхиляється, а при 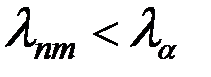 приймається.
приймається. і
і  . По вибірці
. По вибірці  потрібно визначити, яка з цих гіпотез вірна. Нехай
потрібно визначити, яка з цих гіпотез вірна. Нехай  .
. , мінімальне значення похибки другого роду досягається на області, яка визначається нерівністю
, мінімальне значення похибки другого роду досягається на області, яка визначається нерівністю  , де константа вибирається з умови
, де константа вибирається з умови  .
.  являється найбільш потужним.
являється найбільш потужним.

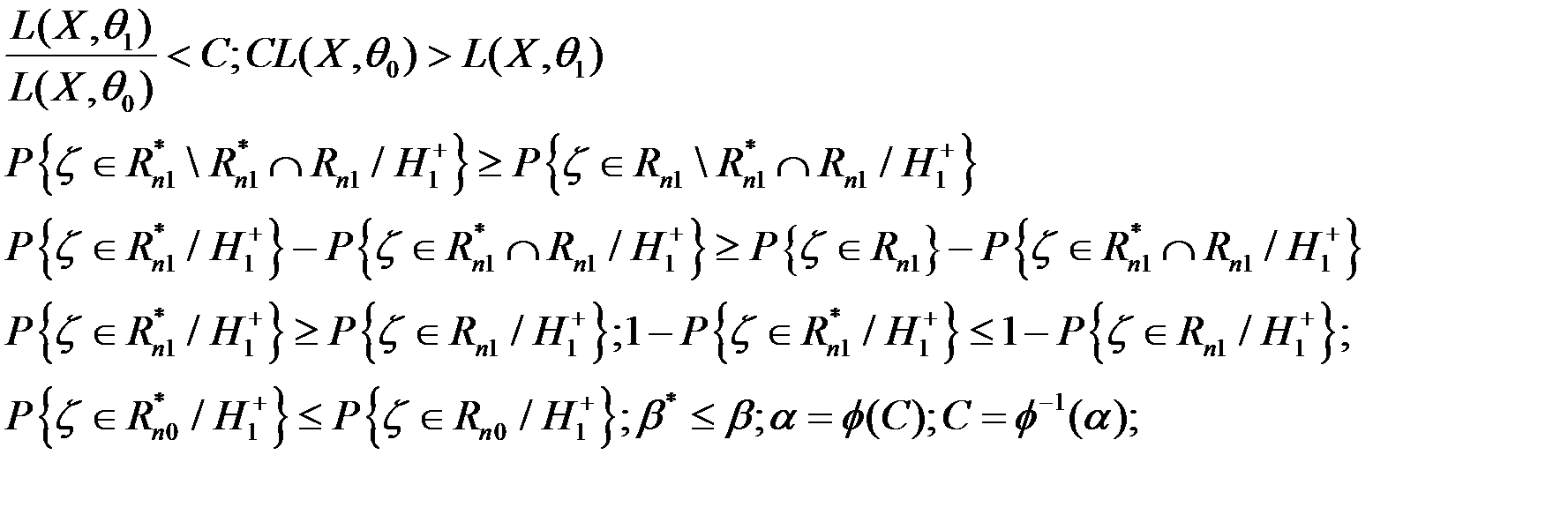
 -фіксоване
-фіксоване 
 потужність критерію
потужність критерію

 -критична область
-критична область


 , тоді серед усіх критеріїв, у яких похибка I роду
, тоді серед усіх критеріїв, у яких похибка I роду  найбільш потужним є критерій з областю
найбільш потужним є критерій з областю

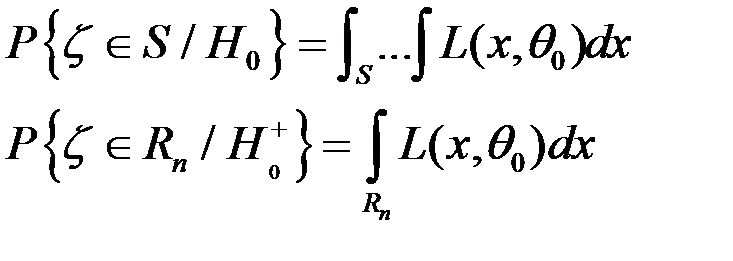
 будь-яка інша критична область, для якої похибка I роду
будь-яка інша критична область, для якої похибка I роду 
 Покажемо
Покажемо 




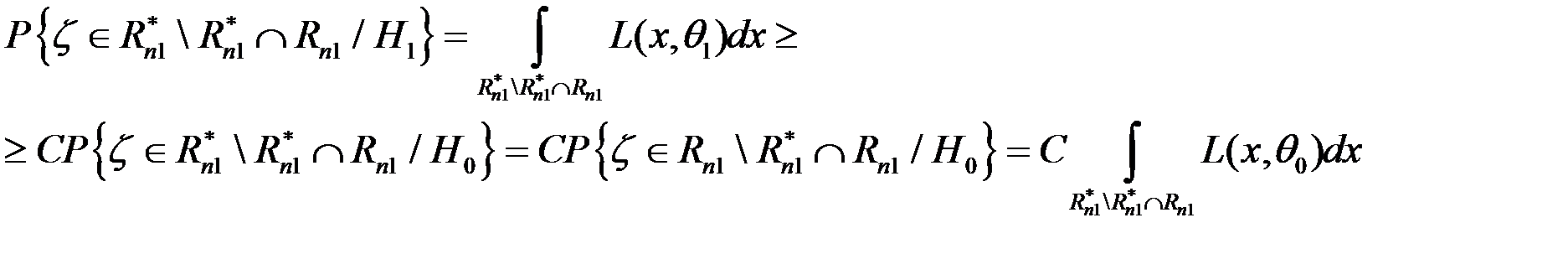

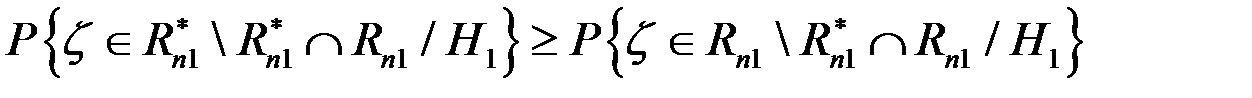



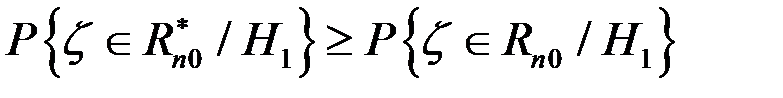






 ;
;  -функція рандомізації
-функція рандомізації
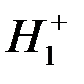
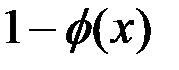






















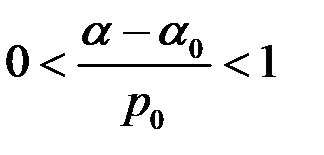
 . Далі вводимо функцію рандомізації:
. Далі вводимо функцію рандомізації:

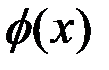 з похиб. І роду
з похиб. І роду  має
має  пох. ІІ роду
пох. ІІ роду


 ~
~  ~
~ 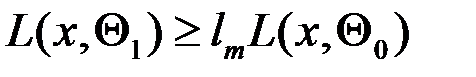
 ~
~  ~
~ 





 та
та  - незалежні випадкові величини. Маємо:
- незалежні випадкові величини. Маємо:



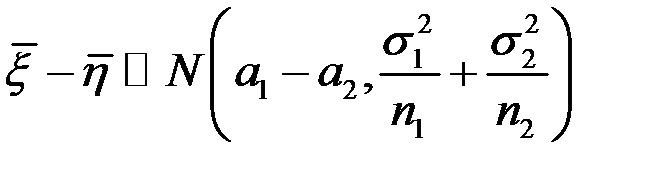



 - невідомі
- невідомі









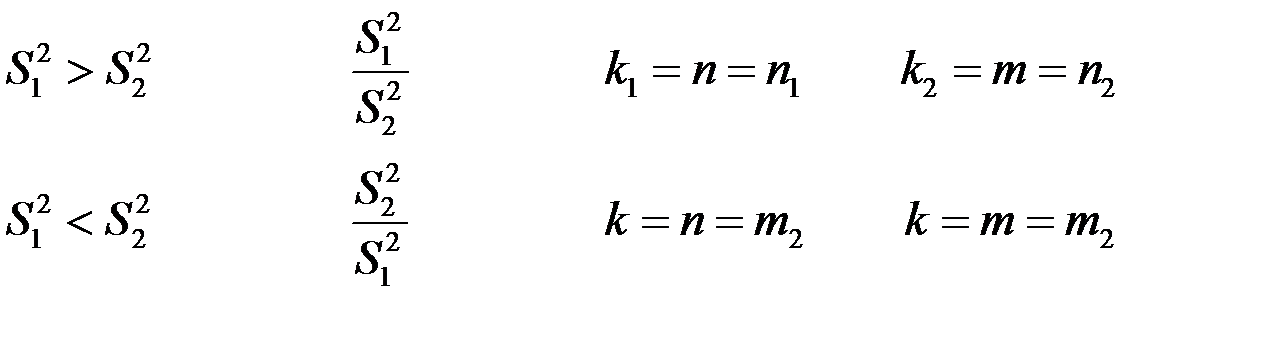
 - невідомі
- невідомі
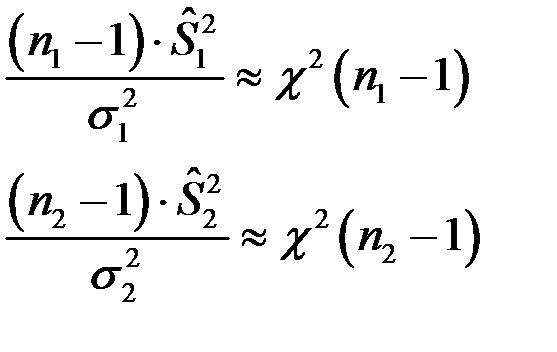

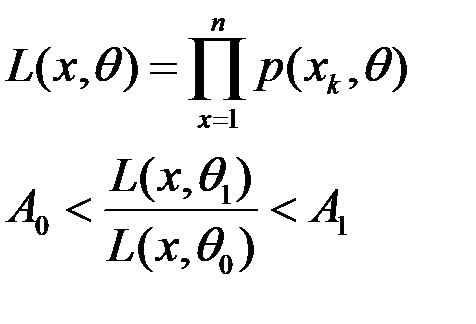




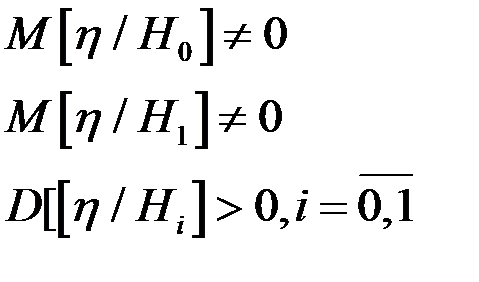

 критерію сили
критерію сили 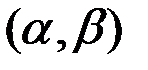 задовольняють наступні нерівності:
задовольняють наступні нерівності:







 ;
; 


 - залежні.
- залежні.  - ф-ція регресії
- ф-ція регресії  по
по  ,
, 
 ,
, 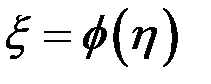 ,
,  .
.  ;
;  ;
;  ;
;  ;
;  ;
; 
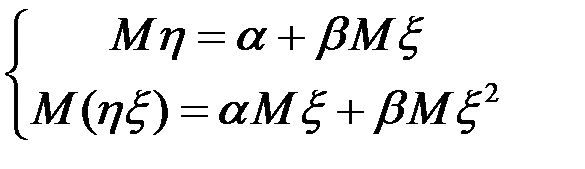 ;
;  ;
; 
 ;
;  ;
;  ;
;  - кореляція;
- кореляція;  .
. - коеф. тісноти зв’язку (корел. віднош.)
- коеф. тісноти зв’язку (корел. віднош.) - найсильн. зв’язок;
- найсильн. зв’язок;  - некорел. велич.
- некорел. велич.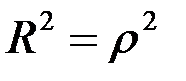







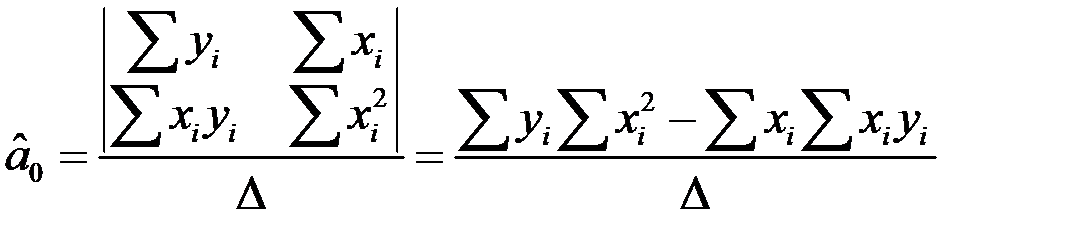

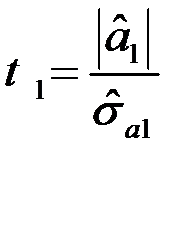



 - ранги
- ранги


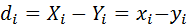 - різниця рангів
- різниця рангів
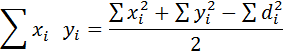
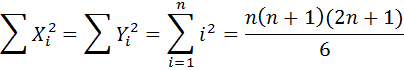
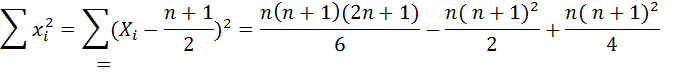


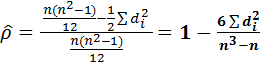 - коефіцієнткореляціїрангівСпірмена
- коефіцієнткореляціїрангівСпірмена


 високий зв’язок
високий зв’язок












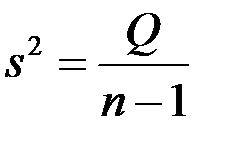 - незмінна оцінка
- незмінна оцінка 
 - дисп. вплив факт. А
- дисп. вплив факт. А  - залишк дисперсія
- залишк дисперсія
 - Фішера-Снедекора
- Фішера-Снедекора 
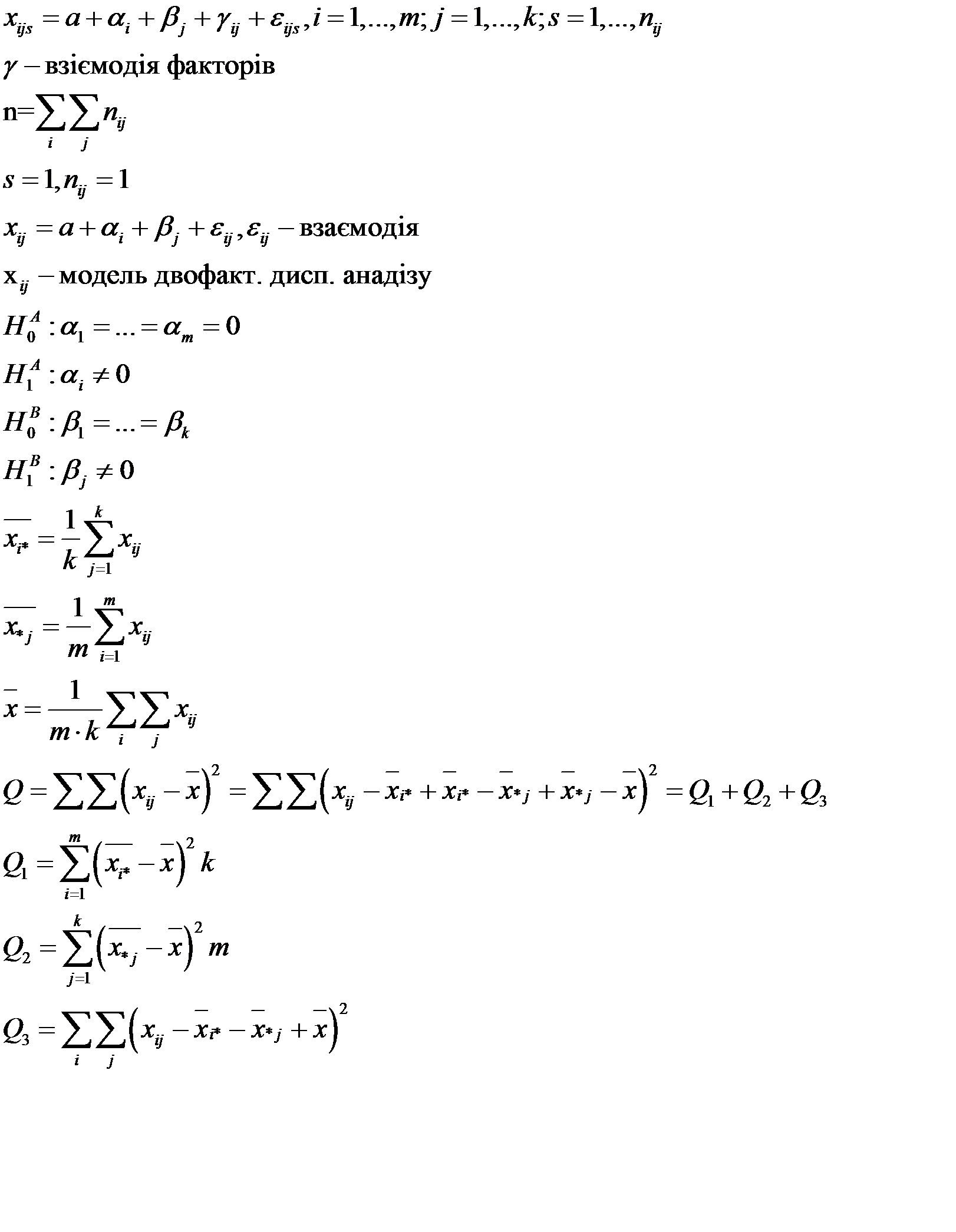


 - щільність
- щільність

 називаєтьсябайєсівськимрішенням (правилом), якщо
називаєтьсябайєсівськимрішенням (правилом), якщо 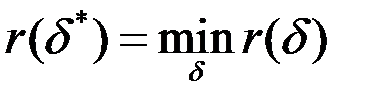
 - апріорний розподіл
- апріорний розподіл - апостеріорний розподіл
- апостеріорний розподіл




 Мінімальні втрати по апоастр.розподілу
Мінімальні втрати по апоастр.розподілу
 - мінімаксне, якщо
- мінімаксне, якщо 


 ,
,  ,
, 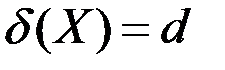 ,
,  ,
, 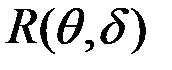
 ,
,  ,
, 

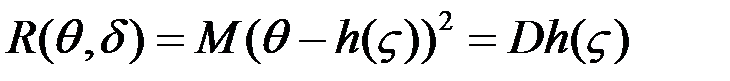



 ,
, 








 Перевірка гіпотез:
Перевірка гіпотез:






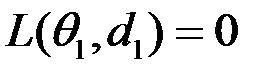
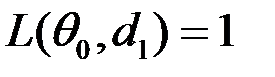


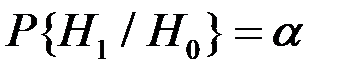





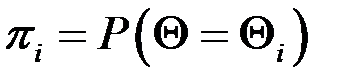
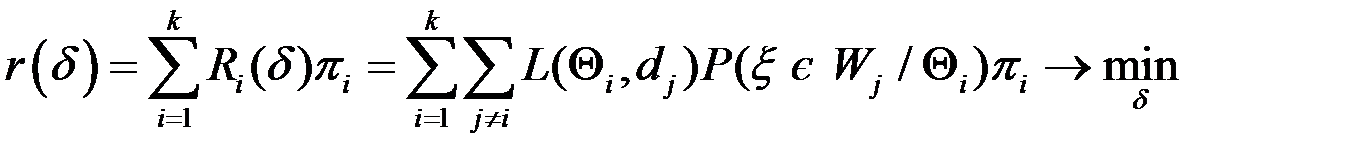
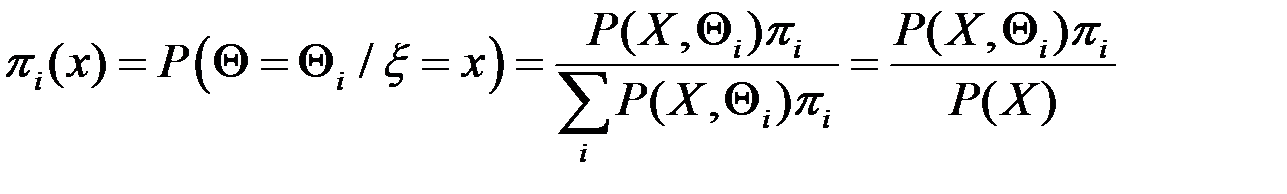

 . Отже, найкраще рішення (байсівське):
. Отже, найкраще рішення (байсівське):




 Яке менше – те рішення і приймаємо:
Яке менше – те рішення і приймаємо:



 x
x 







