Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основна ідея перевірки статистичних гіпотезСодержание книги
Поиск на нашем сайте
Множину Y всіх значень, які може приймати випадкова величина Тn, розіб’ємо на дві неперетинаючихся підмножини Y0 та Y1 (Y = Y0 È Y1) так, щоб імовірність попадання значення статистики Тn у множину Y1 за умови справедливості гіпотези Н0 була достатньо малою. Якщо виявилося, що Тn(x) = Тn(x1, x2, …, xn) Î Y1, то в припущенні справедливості гіпотези Н0 трапилась малоімовірна подія, і ця гіпотеза повинна бути відкинутою як така, що протирічить статистичним даним. У протилежному випадку (тобто якщо Тn(x) Î Y0) немає причин не прийняти гіпотезу Н0, і слід вважати, що спостереження не виявляють протиріч з Н0. Найчастіше імовірність попадання у множину Y1 вибирається рівною або не вищою ніж 0,01 або 0,05 або 0,1. Таку імовірність називають рівнем значущості (a); множину Y1 – критичною областю; Y0 – областю прийняття гіпотези, а правило перевірки – критерієм згоди. Якщо Тn – неперервна випадкова величина, то критична область Y1 задовольняє рівності: P{ Тn Î Y1 | Н0} = a (7.1) де вираз у лівій частині позначає імовірність прийняття статистикою Тn значення у множині Y1 за умови справедливості гіпотези Н0. Зауважимо, що на практиці замість рівності (7.1) часто використовується нерівність (≤) або наближена рівність. Доцільний вибір критичної області, окрім співвідношення (7.1), може залежати ще й від альтернативної гіпотези Н1. Найчастіше за критичну область Y1 вибирають множину:
де В результаті перевірки статистичних гіпотез можуть бути зроблені помилки двох типів. Помилка першого роду полягає в тому, що буде відкинута вірна гіпотеза Н0. Її імовірність a дорівнює Р{ Тn Î Y0 | Н0}, якщо виконується (7.1). У випадку, коли замість (7.1) виконується нерівність (≤) або наближена рівність, імовірність помилки 1-го роду може бути відповідним чином оцінена, а не точно визначена. Помилка другого роду виникає тоді, коли ми приймаємо гіпотезу Н0, в той час, коли справедлива альтернативна гіпотеза. Імовірність b помилки другого роду дорівнює Р{ Тn Î Y1 | Н1}.
Перевірка гіпотези відносно імовірності Нехай А – деяка випадкова подія. Маючи результати n незалежних випробувань, в яких подія А спостерігалась m разів, ми хочемо перевірити гіпотезу, що імовірність події А дорівнює заданому числу р0, тобто Н0 = { P(A)=p0 }. На практиці до цієї гіпотези ми приходимо, наприклад, при перевірці відповідності технологічного процесу заданим умовам (наприклад - відсутності систематичної похибки вимірювань). Нехай гіпотеза Н0 справедлива. Тоді маємо схему Бернуллі: успіх – подія А відбулась; невдача – відбулась подія Kn – число успіхів в n випробуваннях; тоді, як відомо з курсу теорії імовірностей: MKn=np0; DKn=np0q0; q0=1-p0. Користуючись нормальним наближенням біноміального розподілу (теорема Муавра - Лапласа), одержуємо:
(статистика Тn має наближено нормальний розподіл з параметрами 0; 1). При альтернативній гіпотезі Н1 ={ P(A)¹p0 } і рівні значущості a критична область буде мати вигляд:
(для нормального розподілу Ua =-U1-a, Ua - квантиль рівня a Якщо значення статистики Тn, знайдене за вибірковими даними, належить області Y0, то гіпотеза Н0 приймається, в протилежному випадку, коли ТnÎ Y1, то гіпотеза Н0 відхиляється.
Приклад 1. Нехай потрібно перевірити відсутність систематичної похибки терезів, тобто Н0 = { P(п) = P(н)=p0=1/2 }, де P(н) - імовірність недоважування, P(п) - імовірність переважування. В досліді проведено 280 зважувань і із них виявилось 151 недоважувань і 129 переважувань. При справедливості гіпотези Н0 маємо р=1/2; q=1/2 і згідно (7.2) одержимо:
При кількості успіхів (недоважувань) m=151 отримаємо:
Таким чином, Т280 Î Y0 і гіпотеза Н0 приймається (Н0 не суперечить спостереженням). Зауваження. На практиці наведену вище процедуру перевірки гіпотези відносно імовірностей можна використовувати коли n>=50; np>=10.
Перевірка гіпотези про середнє значення нормального розподілу. Критерій Стьюдента Нехай x1, x2, …, xn - ряд незалежних спостережень над випадковою величиною x, яка має нормальний розподіл N(m, s). Параметри m, s - невідомі. Потрібно перевірити гіпотезу H0= { Mx=m0 }, де m0 – деяке задане число. Такого типу задачі часто виникають на практиці, наприклад тоді, коли потрібно визначити наявність систематичних відхилень від номіналу параметрів виробів деякого технологічного процесу. На підставі вибірки обчислимо
Розглянемо статистику
Відомо (див. лаб. роботу № 6), що випадкова величина Tn має розподіл, який називається t - розподілом Стьюдента з (n-1) ступенями волі. Звідси випливає критерій перевірки гіпотези Н0 – критерій Стьюдента. При рівні значущості a вибираємо із таблиць квантилів t-розподілу Стьюдента Тоді при альтернативній гіпотезі Н1 ={ Mx¹m0 } і рівні значущості a критична область відповідно до (7.2) буде мати вигляд:
Допустима область:
Якщо статистика Tn в (7.4) при m=m0 попадає в область Y1, то гіпотезу H0= { Mx=m0 } відхиляємо, якщо Tn Î Y0, то кажемо, що гіпотеза H0 не суперечить експериментальним даним.
Приклад 2. Стьюдент у класичній роботі про t – розподіл наводить наступні дані про додаткові години сну 10 пацієнтів, викликані дією снодійних засобів Таблиця 7.1
Виникає запитання, чи існує істотна різниця між дією снодійних засобів Обчислення згідно формул (7.3) та (7.4) для вибірки При α=0.05 та 9 ступенях волі tкр= Завдання до лабораторної роботи №7 1. Для заданої вибірки x1, x2, …, xn спостережень над випадковою величиною x (див. лаб. роботу №1) перевірити її симетричність відносно середнього значення m. Точніше, гіпотеза полягає в тому, що імовірність прийняття величиною x значення, не більшого від m, дорівнює імовірності прийняття нею значення, не меншого від m (таким чином, обидві імовірності дорівнюють 1/2). Скорочений запис: Нехай: А = { x ≤ m }; тоді Н0 = { P(A)=1/2 }, В якості величини m можна взяти значення Перевірку гіпотези Н0 провести при рівнях значущості a=0,05 та a=0,1. 2. Для заданої вибірки x1, x2, …, xn спостережень над нормально розподіленою випадковою величиною x (див. лаб. роботу № 6) перевірити гіпотезу H0= { Mx=m0 } при рівнях значущості a=0,05 та a=0,1. За величину m0 взяти значення m0 = (xmin+ xmax)/2.
Контрольні питання до лабораторної роботи №7 1. Дати пояснення основних понять перевірки статистичних гіпотез: основна гіпотеза, статистика критерія, рівень значущості, критична і допустима області, помилки 1-го і 2-го роду. 2. Навести загальну схему перевірки гіпотез.
ЛАБОРАТОРНА РОБОТА № 8 Тема: Перевірка статистичних гіпотез - 2. Гіпотеза про нормальність розподілу імовірностей Мета роботи: Навчитися перевіряти гіпотези про нормальність розподілу випадкової величини Теоретичні відомості Випадкова величина має нормальний розподіл (позначення x
де μ, s - деякі числа. Імовірнісний зміст параметрів μ, s: μ – математичне сподівання випадкової величини x, s - середнє квадратичне відхилення випадкової величини x.
Рис.8.1
Припустимо, що є заданою вибірка значень x1, x2, …, xn випадкової величини x, отримана при тих чи інших спостереженнях. Треба вирішити, чи можна на підставі наявних даних зробити обгрунтоване припущення про нормальність розподілу величини x (інакше – про нормальність теоретичного розподілу імовірностей). Таким чином, мова йде про перевірку гіпотези Н0={теоретичний розподіл імовірностей є нормальним}, або скорочено: H0 = { x (позначення N(·, ·) замість N(μ, σ) вживається, коли мова йде про нормальність розподілу взагалі, без припущень щодо конкретних значень параметрів цього розподілу). З багатьох відомих критеріїв узгодження емпіричних даних з гіпотезою про нормальність теоретичного розподілу в даній роботі треба використати лише два. Основні принципи, на яких базуються вказані критерії і відповідні дії, що потрібно виконати, формулюються нижче.
1. Візуальний аналіз графічного зображення вибірки При візуальному дослідженні графічного зображення вибірки(“стеблина з листям”, гістограми, полігони) необхідно звернути увагу на відповідність побудованих рисунків графіку щільності нормального розподілу. Показниками доброї відповідності є: а) наявність однієї вибіркової моди, відносно якої розташування даних майже симетричне; б) поступове спадання графіків до нульового значення при віддаленні від модального значення. а) наявність явної полімодальності (тобто наявність декількох модальних значень); б) явна асиметрія у побудованих графіках; в) наявність обривчастих кінців у графіках вибіркових розподілів. За даними візуального аналізу графічних зображень вибірки можна дати висновок відносно гіпотези нормальності розподілу в наступних термінах: а) добра відповідність; б) погана відповідність; в) нема підстав як для позитивної так і для негативної відповіді.
2. Порівняння вибіркових та очікуваних частот. Критерій c2. Одним з основних способів перевірки гіпотези про нормальність є порівняння вибіркових та очікуваних частот. Гіпотезу потрібно відхилити, якщо ці частоти сильно відрізняються між собою. Одним з варіантів втілення цієї ідеї є критерій c2. Гіпотеза, що перевіряється: H0 = {x ~ N(·, ·) }, причому параметри μ і s невідомі. Для використання критерію c2 у нашому випадку необхідно спочатку знайти оцінки невідомих μ і s. За оцінки цих параметрів візьмемо відповідно вибіркове середнє Потім числову вісь розіб’ємо на інтервали так, щоб в кожному з них знаходилось би не менше ніж 8 вибіркових значень. Так, зокрема, для знаходження кінців інтервалів групування можна використати деякі з кінців інтервалів групування, визначених в лабораторній роботі №2. Приклад 1. Нехай вибірка задається таблицею “групування - частоти”.
Таблиця 8.1
На інтервалі На цьому інтервалі тільки 3 вибіркових значення, що нас не влаштовує. Приєднаємо до розглянутого наступний інтервал групування Таблиця 8.2
Статистика критерію Tn,r обчислюється за формулою:
де n – об’єм вибірки; mi – кількість вибіркових значень, що належать і-му інтервалу; pi – імовірність того, що випадкова величина (з розподілом N( (Нагадуємо, що імовірність влучення випадкової величини x ~ N(
де функція
Замість функції ψ Зауваження. При розрахунках слід врахувати, що на відміну від рівностей для функції
для функції ψ мають місце співвідношення: ψ
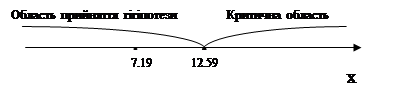
Можна вважати, що статистика Tn,r при n > 50 добре наближується розподілом c2r-3 (розподілом c2 з r-3 ступенями волі). Критична область для критерія c2 правостороння. Відповідними критичними точками є точки U1-a - квантиль розподілу c2 з r-3 ступенями волі рівня 1-a, де a - заданий рівень значущості. Приклад 2. Нехай рівень значущості a = 0.05 і нам потрібно перевірити гіпотезу про нормальність вибірки, відносно якої відомо, що Таблиця 8.3
Значення Tn,r= T200,9=7,19. Критичною точкою є
Значення статистики критерію 7.19 належить області прийняття гіпотези. Завдяки цьому можна стверджувати, що дані не протирічать гіпотезі про нормальність вибірки.
Завдання до лабораторної роботи №8 Зауваження.Для виконання роботи використовувати вибірку з лабораторної роботи №1. 1. Провести візуальний аналіз графічного зображення вибірки. Зробити висновок про відповідність вибіркових даних гіпотезі, що висунута. 2. Перевірити гіпотезу про нормальність розподілу імовірностей за допомогою критерію c2 (α = 0.1, α = 0.05).
Контрольні питання до лабораторної роботи №8 1. Що означає: випадкова величина має нормальний розподіл? 2. Який імовірнісний зміст числових параметрів, що входять до виразу щільності нормального розподілу? 3. Як відбувається візуальна перевірка вибірки на нормальність? 4. Сформулювати основні положення методики c2 перевірки статистичних гіпотез окремо для випадків простої і складної основної гіпотези. 5. Яка саме гіпотеза перевіряється у даній роботі? Чи є вона простою, чи складною? Чому кількість ступенів волі розподілу c2 дорівнює тут саме r-3? 6. Сформулювати основні теоретичні положення, на яких базується методика c2 (граничні теореми К. Пірсона та Р. Фішера). 7. Сформулювати основні положення методу c2 при перевірці нормальності теоретичного розподілу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.009 с.) |

 (правосторонній критерій)
(правосторонній критерій) (лівосторонній критерій)
(лівосторонній критерій) (двосторонній критерій)
(двосторонній критерій) - квантиль рівня a умовного розподілу статистики Тn (умовного в припущенні справедливості Н0). Точки, які розділяють множини Y0 та Y1, називають критичними точками.
- квантиль рівня a умовного розподілу статистики Тn (умовного в припущенні справедливості Н0). Точки, які розділяють множини Y0 та Y1, називають критичними точками. .
. (7.2)
(7.2)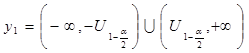 (7.3)
(7.3)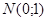 -розподілу). Область прийняття гіпотези у0 – це інтервал (
-розподілу). Область прийняття гіпотези у0 – це інтервал (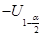 ,
,  ).
). Виберемо рівень значущості a=0,05, тоді 1-a/2=0,975; U0,975=1,96 – квантиль рівня 0,975 N(0;1)-розподілу. Тоді із рівності (7.3) одержуємо критичну область
Виберемо рівень значущості a=0,05, тоді 1-a/2=0,975; U0,975=1,96 – квантиль рівня 0,975 N(0;1)-розподілу. Тоді із рівності (7.3) одержуємо критичну область  . Допустима область Y0 = (-1,96, 1,96).
. Допустима область Y0 = (-1,96, 1,96). .
.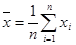 ,
,  (7.3)
(7.3)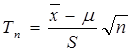 (7.4)
(7.4) - квантиль рівня
- квантиль рівня  розподілу Стьюдента з (n-1) ступенями волі.
розподілу Стьюдента з (n-1) ступенями волі. (7.5)
(7.5) .
. та
та  .
. буде вибіркою об’єму n=10 нормального розподілу N(0, σ) при умові справедливості гіпотези H0= { Mx=0 }, тобто коли між снодійними засобами X та Y немає різниці. При цій же умові величина
буде вибіркою об’єму n=10 нормального розподілу N(0, σ) при умові справедливості гіпотези H0= { Mx=0 }, тобто коли між снодійними засобами X та Y немає різниці. При цій же умові величина  має t – розподіл Стьюдента з 9 ступенями волі;
має t – розподіл Стьюдента з 9 ступенями волі;  ,
, 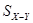 - відповідно середнє значення та вибіркове середнє квадратичне відхилення вибірки
- відповідно середнє значення та вибіркове середнє квадратичне відхилення вибірки  .
. =2.26, тоді
=2.26, тоді  . Ясно, що
. Ясно, що 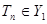 і гіпотезу Н0 відхиляємо, тобто різниця між снодійними засобами
і гіпотезу Н0 відхиляємо, тобто різниця між снодійними засобами 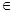 N(μ, s)), якщо її щільність розподілу
N(μ, s)), якщо її щільність розподілу 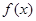 визначається за формулою:
визначається за формулою: ,
, Графік щільності розподілу випадкової величини x має дзвіноподібну форму і є симетричним відносно прямої х= μ (див. рис.8.1)
Графік щільності розподілу випадкової величини x має дзвіноподібну форму і є симетричним відносно прямої х= μ (див. рис.8.1)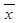 та вибіркове середнє квадратичне відхилення s, отримані за згрупованою вибіркою (див. лаб. роботу № 4).
та вибіркове середнє квадратичне відхилення s, отримані за згрупованою вибіркою (див. лаб. роботу № 4).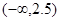 немає вибіркових значень. Тому спочатку необхідно розглянути інтервал
немає вибіркових значень. Тому спочатку необхідно розглянути інтервал 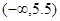 .
. і розглянемо інтервал
і розглянемо інтервал  . У цей інтервал попадає 5 вибіркових значень, що також нас не влаштовує. Якщо розглянемо інтервал
. У цей інтервал попадає 5 вибіркових значень, що також нас не влаштовує. Якщо розглянемо інтервал 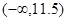 , то одержимо в ньому 8.5 вибіркових значень. Таким чином, перша точка нового групування b1=11.5. Наступним буде інтервал
, то одержимо в ньому 8.5 вибіркових значень. Таким чином, перша точка нового групування b1=11.5. Наступним буде інтервал  , який містить 10.5 значеньі за b2 беремо значення 17.5. Продовжуючи аналогічним чином, одержуємо вторинне групування (див. табл.. 8.2).
, який містить 10.5 значеньі за b2 беремо значення 17.5. Продовжуючи аналогічним чином, одержуємо вторинне групування (див. табл.. 8.2).
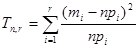 ,
,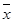 , S)) належить і-му інтервалу;
, S)) належить і-му інтервалу;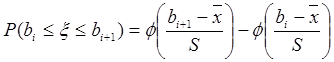 ,
,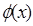 - це інтеграл імовірностей:
- це інтеграл імовірностей: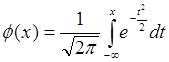 .
.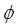 можна використовувати функцію
можна використовувати функцію  ψ:
ψ: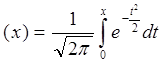 .
.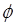 :
: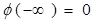 ,
, 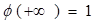 ,
,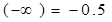 , ψ
, ψ  .
.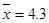 ; S=9.71; n=200 і яка задається таблицею:
; S=9.71; n=200 і яка задається таблицею: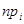
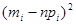
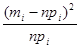
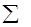

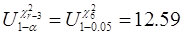 (див. додаток. № 4 до методичних вказівок).
(див. додаток. № 4 до методичних вказівок).