Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії якості точкових статистичних оцінокСодержание книги
Поиск на нашем сайте
Критерії якості точкових статистичних оцінок Статистична оцінка qn* параметру q називається незсуненою, якщо М(qn* ) = q. З двох статистичних незсунених оцінок параметру q ефективнішою називається та, дисперсія якої менше. Статистична оцінка qn* параметру q називається обґрунтованою, якщо при Існує багато методів знаходження точкових статистичних оцінок. Серед таких методів одними з найбільш відомих є метод максимальної правдоподібності (або максимуму правдоподібності) та метод підстановки емпіричного розподілу. Не завжди різні методи дають одні і ті ж рекомендації щодо оцінювання одного і того ж параметру. Втім, обидва названі вище методи призводять до однакової оцінки таких параметрів як математичне сподівання і дисперсія. Нижче наводяться конкретні інструкції відносно оцінювання цих та деяких інших параметрів теоретичного розподілу. Обчислення статистичних оцінок основних числових параметрів випадкової величини 1) Оцінка математичного сподівання Для незгрупованої вибірки вибірковим середнім називають статистику Для згрупованої вибірки вибірковим середнім називають статистику (тут
Вибіркове середнє використовується як оцінка теоретичного математичного сподівання Мξ. Величина 2) Оцінка дисперсії та середнього квадратичного відхилення Для незгрупованої вибірки: - вибірковою дисперсією називають статистику
- другим вибірковим центральним моментом називають статистику
Для згрупованої вибірки: - вибірковою дисперсією називають статистику
- другим вибірковим центральним моментом називають статистику
де fi - абсолютна частота,
Вибірковим середнім квадратичним відхиленням називається статистика 3) Оцінка медіани Для незгрупованої вибірки для оцінки med x розглядається елемент рангу Для згрупованої вибірки для знаходження оцінки медіани необхідно знайти абсциссу точки перетину прямої у=0,5 та графіка функції кумулятивних відносних частот (див. лаб. роботу №3). На рисунку 4.1 зображено знаходження медіани для згрупованої вибірки.
Рис.4.1
4) Оцінка моди Для незгрупованої вибірки за оцінкн моди mоd x приймається вибірковий елемент, що має найбільшу частоту (див. таблицю частот в лаб. роб. №1) і позначається mоd. Для згрупованої вибірки для обчислення моди використовується формула
де m – номер модального інтервалу групування (тобто того, який містить максимальну кількість вибіркових значень); h = am+1- am; d = | fm-fm-1 |; d¢ = | fm+1-fm |. Зміст формули (4.1) зрозуміло з рисунку 4.2.
Зауважимо, що якщо fm-1= fm= fm+1, то права частина формули (4.1) не визначена. В цьому випадку покладають:
Якщо m=1 або m=k, то у першому випадку покладають fm-1=0, а в другому fm+1=0.
Симетричність вибірки Якщо випадкова величина x має симетричний розподіл, то слід сподіватися, що вибірка, отримана при дослідженні x, також симетрична, тобто “симетрично” розсіяна навколо деякого центру. Ознакою симетричності вибірки є так зване емпіричне правило Юла: симетрична вибірка повинна мати одну моду, яка може бути обчислена за формулою:
Для конкретності наближену рівність розуміємо так: вибіркова мода відрізняється від моди, отриманої за формулою (4.2), не більше, ніж на 10% від середнього квадратичного відхилення.
Завдання до лабораторної роботи №4 Зауваження. Для виконання роботи використовувати вибірку з лабораторної роботи №1. 1. Обчислити за незгрупованою та згрупованою вибіркою 2. Результати обчислень занести в таблицю:
3. Оцінити за правилом Юла симетричність вибірки.
Контрольні питання до лабораторної роботи №4 1. Що таке статистична оцінка числового параметру випадкової величини? 2. Назвіть відомі вам критерії якості статистичних оцінок. 3. Що таке збіжність за імовірністю? 4. Чому статистичну оцінку ми вважаємо випадковою величиною? 5. Що таке статистика? 6. Які числові параметри можуть прийматися за центр розсіювання випадкової величини? 7. Що таке математичне сподівання випадкової величини? Сформулюйте основні властивості математичного сподівання. 8. Яку статистику приймають за оцінку математичного сподівання? 9. Довести, що величина 10. Що таке дисперсія? Назвіть основні властивості дисперсії. Що характеризує дисперсія? Як оцінити її за вибіркою? 11. Які статистики наближують середнє квадратичне відхилення? 12. Що таке медіана випадкової величини? Як оцінюється медіана за вибіркою? 13. Що таке мода випадкової величини? 14. Що є ознакою симетричності вибірки? 15. Назвіть відомі вам методи точкового статистичного оцінювання та сформулюйте, в чому саме вони полягають.
ЛАБОРАТОРНА РОБОТА №5 Тема: Статистичні оцінки квантилів Мета роботи: Навчитися оцінювати квантилі та процентилі розподілів за вибірковими даними Теоретичні відомості. Означення. Квантилем рівня a (0 < a < 1) у випадку неперервних розподілів називається число Ua, яке є найменшим розв’язком рівняння Геометрично це означає, що квантиль рівня a - це найменша з абсцис точок перетину прямої у=a з графіком функції у= Зауваження. При означенні квантиля рівня a слова “найменший розв’язок” необхідно для усунення неоднозначності, яка може виникати при розв’язанні рівняння
Рис. 5.1
Означення. Процентилем рівня a (0 < a < 100) називається число Qa, яке зв’язано з квантилем співвідношенням: Qa= U(a/100) Так, наприклад, Q30= U0,3; Q50= U0,5. Вибірковий квантиль рівня a - це число тобто імовірність того, що випадкова величина x під час експерименту прийме значення менше за число Ua, дорівнює a. (Наприклад, якщо U0,3=-7, то P(x<-7) = 0,3.) Вибіркові квантилі (процентилі)
Знаходження вибіркових квантилів (процентилів) - за незгрупованою вибіркою Для знаходження вибіркового квантиля (процентиля) рівня a треба спочатку знайти ранг цього квантиля (процентиля). В літературі можна знайти різні вирази з цього приводу. В даній роботі рекомендуються наступні формули:
де Наприклад, якщо a=0,3, n=80, то маємо: Якщо ранг вибіркового елемента відомий, то легко знайти відповідний вибірковий елемент (див. лаб. роботу №1). - за згрупованою вибіркою Будемо знаходити вибіркові квантилі (процентилі) графічним способом. Для цього використаємо графік кумулятивної функції розподілу відносних частот (див. лаб. роботу №3). На рівні, що відповідає заданому числу a, проведемо пряму у=a до перетину з кумулятою. Найменша з абсцис точок перетину графіків – шуканий квантиль (див. рис. 5.1). Зауваження. При проведенні прямої у=a необхідно узгодити рівень a з одиницями, в яких проградуйована вісь Оу. Якщо вісь Оу проградуйована в процентах, то a - рівень квантиля – необхідно помножити на 100, а рівень процентиля залишити без змін.
Завдання до лабораторної роботи №5 Зауваження. Для виконання роботи використовувати вибірку з лабораторної роботи №1. 1. Знайти ранги 2. Знайти по незгрупованій вибірці 3. Знайти графічно по згрупованій вибірці 4. Результати занести в таблицю:
Контрольні питання до лабораторної роботи №5 1. Що таке квантиль (процентиль) рівня a у випадку неперервних розподілів? 2. Який статистичний та імовірнісний зміст квантиля рівня a? 3. Як зв’язані між собою квантилі і процентилі? 4. Яка частина вибірки лежить між числами 5. Якому методу статистичного точкового оцінювання відповідає графічний спосіб за згрупованою вибіркою?
ЛАБОРАТОРНА РОБОТА № 6 Тема: Інтервальні оцінки параметрів нормально розподіленої випадкової величини Мета роботи: Навчитися будувати довірчі інтервали різних рівнів для невідомих математичного сподівання та дисперсії нормально розподіленої випадкової величини. Теоретичні відомості. У попередній роботі вивчалися точкові оцінки невідомих числових параметрів випадкової величини, тобто оцінки, що задавалися одним числом. Якщо оцінка q* наближувала параметр q, то виникало питання, наскільки точне це наближення, тобто яке відхилення q* від q. Додатнє число d, для якого виконується рівність | q*- q | < d характеризує точність оцінки q* для параметру q. Чим менше число d, тим краще оцінка q* наближує q. Але q* - випадкова величина, та й параметр q невідомий. Тому про нерівність | q*- q | < d (або її еквівалент q*- d < q < q* + d) можна говорити лише з деякою імовірністю. Треба навчитися будувати інтервали, які накриють шукані параметри з потрібною імовірністю. Означення. Довірчим інтервалом рівня a (0 < a < 1) для невідомого параметру q називають числовий інтервал [x1, x2], який накриває невідомий параметр q з імовірністю (1-a), тобто P{ q Î [x1, x2] } = 1-a (6.1) Число (1-a) називають надійністю, або довірчою імовірністю відповідного інтервалу. При побудові довірчих інтервалів число a задається заздалегідь. Найчастіше за a береться одне з чисел a=0,1 або a=0,05 або a=0,01. Тоді відповідні надійності: 0,9 або 0,95 або 0,99. Відзначимо, що інтервальні оцінки невідомих параметрів задаються двома числами x1, x2 - початком і кінцем інтервалу, якому повинен належати невідомий параметр з відповідною імовірністю. Означення. Нехай x1, x2,..., xn – незалежні за означенням випадкові величини, кожна з яких має розподіл N(0;1). Тоді, за означенням, випадкова величина x = x12 + x22 +... + xn2 має розподіл c2 з n ступенями волі (позначення x ~ cn2). Означення. Нехай x1 та x2 - незалежні випадкові величини, причому x1 ~ N(0;1), а x2 ~ cn2. Тоді, за означенням, випадкова величина
Побудова довірчих інтервалів для невідомих математичного сподівання та дисперсії нормально розподіленої випадкової величини базується на теоремі: Якщо x1, x2, …, xn - вибірка, отримана при дослідженні випадкової величини x ~ N(μ; σ), то: 1) статистики (нагадаємо, що 2) За допомогою цієї теореми легко довести, що за умови вивчення випадкової величини x ~ N(μ; σ): а) довірчим інтервалом рівня a для математичного сподівання є інтервал
де б) довірчим інтервалом рівня a для дисперсії є інтервал
де
Завдання до лабораторної роботи № 6 1. Отримати вибірку згідно своєму варіанту (див. додаток 2 до методичних вказівок). 2. Обчислити 3. Знайти довірчі інтервали рівня 0,05 та 0,1 для невідомого математичного сподівання (для знаходження квантилів t-розподілу див. додаток 3). 4. Знайти довірчі інтервали рівня 0,05 та 0,1 для невідомої дисперсії (для знаходження квантилів c2-розподілу див. додаток 4). 5. Результати обчислень занести в таблицю:
Контрольні питання до лабораторної роботи №6 1. Що таке інтервальна оцінка? Чим вона відрізняється від точкової? 2. Як розуміти термін “точність оцінки”? Чому про точність інтервальної оцінки можна говорити лише з деякою імовірністю? 3. Що таке довірчий інтервал рівня a для невідомого параметра? 4. Пояснити зміст рівності (6.1). 5. За допомогою якої теореми будуються довірчі інтервали для невідомих математичного сподівання та дисперсії нормально розподіленої випадкової величини? 6. Як знайти вибіркову дисперсію, якщо відомі відповідні довірчі інтервали та об’єм вибірок?
ЛАБОРАТОРНА РОБОТА № 7 Тема: Перевірка статистичних гіпотез I. Гіпотези відносно імовірностей та середніх значень Мета роботи: Ознайомитися з задачами перевірки статистичних гіпотез на простих прикладах перевірки гіпотез відносно імовірностей та середніх значень. Теоретичні відомості Теоретичні відомості Випадкова величина має нормальний розподіл (позначення x
де μ, s - деякі числа. Імовірнісний зміст параметрів μ, s: μ – математичне сподівання випадкової величини x, s - середнє квадратичне відхилення випадкової величини x.
Рис.8.1
Припустимо, що є заданою вибірка значень x1, x2, …, xn випадкової величини x, отримана при тих чи інших спостереженнях. Треба вирішити, чи можна на підставі наявних даних зробити обгрунтоване припущення про нормальність розподілу величини x (інакше – про нормальність теоретичного розподілу імовірностей). Таким чином, мова йде про перевірку гіпотези Н0={теоретичний розподіл імовірностей є нормальним}, або скорочено: H0 = { x (позначення N(·, ·) замість N(μ, σ) вживається, коли мова йде про нормальність розподілу взагалі, без припущень щодо конкретних значень параметрів цього розподілу). З багатьох відомих критеріїв узгодження емпіричних даних з гіпотезою про нормальність теоретичного розподілу в даній роботі треба використати лише два. Основні принципи, на яких базуються вказані критерії і відповідні дії, що потрібно виконати, формулюються нижче.
1. Візуальний аналіз графічного зображення вибірки При візуальному дослідженні графічного зображення вибірки(“стеблина з листям”, гістограми, полігони) необхідно звернути увагу на відповідність побудованих рисунків графіку щільності нормального розподілу. Показниками доброї відповідності є: а) наявність однієї вибіркової моди, відносно якої розташування даних майже симетричне; б) поступове спадання графіків до нульового значення при віддаленні від модального значення. а) наявність явної полімодальності (тобто наявність декількох модальних значень); б) явна асиметрія у побудованих графіках; в) наявність обривчастих кінців у графіках вибіркових розподілів. За даними візуального аналізу графічних зображень вибірки можна дати висновок відносно гіпотези нормальності розподілу в наступних термінах: а) добра відповідність; б) погана відповідність; в) нема підстав як для позитивної так і для негативної відповіді.
2. Порівняння вибіркових та очікуваних частот. Критерій c2. Одним з основних способів перевірки гіпотези про нормальність є порівняння вибіркових та очікуваних частот. Гіпотезу потрібно відхилити, якщо ці частоти сильно відрізняються між собою. Одним з варіантів втілення цієї ідеї є критерій c2. Гіпотеза, що перевіряється: H0 = {x ~ N(·, ·) }, причому параметри μ і s невідомі. Для використання критерію c2 у нашому випадку необхідно спочатку знайти оцінки невідомих μ і s. За оцінки цих параметрів візьмемо відповідно вибіркове середнє Потім числову вісь розіб’ємо на інтервали так, щоб в кожному з них знаходилось би не менше ніж 8 вибіркових значень. Так, зокрема, для знаходження кінців інтервалів групування можна використати деякі з кінців інтервалів групування, визначених в лабораторній роботі №2. Приклад 1. Нехай вибірка задається таблицею “групування - частоти”.
Таблиця 8.1
На інтервалі На цьому інтервалі тільки 3 вибіркових значення, що нас не влаштовує. Приєднаємо до розглянутого наступний інтервал групування Таблиця 8.2
Статистика критерію Tn,r обчислюється за формулою:
де n – об’єм вибірки; mi – кількість вибіркових значень, що належать і-му інтервалу; pi – імовірність того, що випадкова величина (з розподілом N( (Нагадуємо, що імовірність влучення випадкової величини x ~ N(
де функція
Замість функції ψ Зауваження. При розрахунках слід врахувати, що на відміну від рівностей для функції
для функції ψ мають місце співвідношення: ψ
Можна вважати, що статистика Tn,r при n > 50 добре наближується розподілом c2r-3 (розподілом c2 з r-3 ступенями волі). Критична область для критерія c2 правостороння. Відповідними критичними точками є точки U1-a - квантиль розподілу c2 з r-3 ступенями волі рівня 1-a, де a - заданий рівень значущості. Приклад 2. Нехай рівень значущості a = 0.05 і нам потрібно перевірити гіпотезу про нормальність вибірки, відносно якої відомо, що Таблиця 8.3
Значення Tn,r= T200,9=7,19. Критичною точкою є
Значення статистики критерію 7.19 належить області прийняття гіпотези. Завдяки цьому можна стверджувати, що дані не протирічать гіпотезі про нормальність вибірки.
Завдання до лабораторної роботи №8 Зауваження.Для виконання роботи використовувати вибірку з лабораторної роботи №1. 1. Провести візуальний аналіз графічного зображення вибірки. Зробити висновок про відповідність вибіркових даних гіпотезі, що висунута. 2. Перевірити гіпотезу про нормальність розподілу імовірностей за допомогою критерію c2 (α = 0.1, α = 0.05).
Контрольні питання до лабораторної роботи №8 1. Що означає: випадкова величина має нормальний розподіл? 2. Який імовірнісний зміст числових параметрів, що входять до виразу щільності нормального розподілу? 3. Як відбувається візуальна перевірка вибірки на нормальність? 4. Сформулювати основні положення методики c2 перевірки статистичних гіпотез окремо для випадків простої і складної основної гіпотези. 5. Яка саме гіпотеза перевіряється у даній роботі? Чи є вона простою, чи складною? Чому кількість ступенів волі розподілу c2 дорівнює тут саме r-3? 6. Сформулювати основні теоретичні положення, на яких базується методика c2 (граничні теореми К. Пірсона та Р. Фішера). 7. Сформулювати основні положення методу c2 при перевірці нормальності теоретичного розподілу.
Таблиця значень функції Лапласа (в наведених в таблиці значеннях функції перші 0 і точка опущені)
Література 1. Крамер Г. Математические методы статистики. – М.: Миp, 1975. – 648 с. 2. Мелник М. Основы прикладной с
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.52.54 (0.015 с.) |

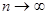 оцінка qn* прямує до числа q за імовірністю, тобто
оцінка qn* прямує до числа q за імовірністю, тобто 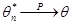 при
при 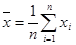 . (4.1)
. (4.1)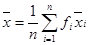 (4.2)
(4.2)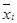 - середні точки інтервалів групування;
- середні точки інтервалів групування; - абсолютні частоти цих інтервалів).
- абсолютні частоти цих інтервалів).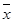 , обчислена за формулою (4.1), є незсуненою обґрунтованою оцінкою Мξ.
, обчислена за формулою (4.1), є незсуненою обґрунтованою оцінкою Мξ.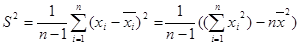 ; (4.3)
; (4.3)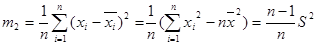 (4.4)
(4.4)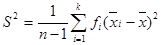 ; (4.5)
; (4.5)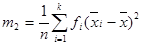 (4.6)
(4.6)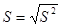 . Статистики
. Статистики 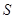 та
та 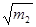 є статистичними оцінками середнього квадратичного відхилення sx випадкової величини x.
є статистичними оцінками середнього квадратичного відхилення sx випадкової величини x.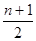 (див. лаб. роботу №1), який називається вибірковою медіаною і позначається med або medх.
(див. лаб. роботу №1), який називається вибірковою медіаною і позначається med або medх.
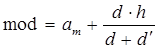 , (4.7)
, (4.7)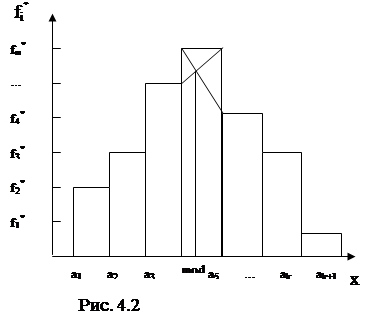
 .
.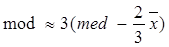 (4.8)
(4.8) , S2, S, m2,
, S2, S, m2, 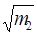 , med, mod,
, med, mod, 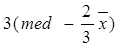 . Згруповану вибірку взяти із лабораторної роботи №2 (завдання №1).
. Згруповану вибірку взяти із лабораторної роботи №2 (завдання №1).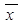 , обчислена за формулою (4.1), є обґрунтованою незсуненою оцінкою математичного сподівання.
, обчислена за формулою (4.1), є обґрунтованою незсуненою оцінкою математичного сподівання. = a, де
= a, де 
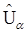 , яке має ту властивість, що приблизно a-частина вибіркових даних менше за число
, яке має ту властивість, що приблизно a-частина вибіркових даних менше за число 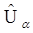 . Аналогічну властивість має вибірковий процентиль
. Аналогічну властивість має вибірковий процентиль  : менше за
: менше за 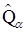 приблизно a% вибірки. Дане означення вибіркового квантиля (процентиля) пов’язане з тією властивістю теоретичного квантиля, що для неперервної випадкової величини x квантиль рівня a задовольняє умові: P(x<Ua) = a,
приблизно a% вибірки. Дане означення вибіркового квантиля (процентиля) пов’язане з тією властивістю теоретичного квантиля, що для неперервної випадкової величини x квантиль рівня a задовольняє умові: P(x<Ua) = a,
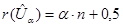 (для квантилів) (5.1)
(для квантилів) (5.1)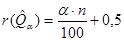
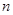 – об’єм вибірки.
– об’єм вибірки.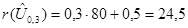 .
.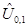 ,
, 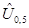 ,
, 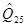 ,
, 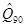 .
.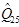 ,
,  має розподіл Стьюдента з n ступенями волі (позначення h ~ tn).
має розподіл Стьюдента з n ступенями волі (позначення h ~ tn). та S2 - незалежні
та S2 - незалежні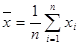 ;
;  ) ;
) ;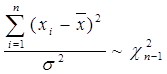 ; 3)
; 3) 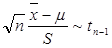 .
.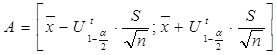 ,
, - квантиль рівня 1-a/2 розподілу Стьюдента з n-1 ступенями волі;
- квантиль рівня 1-a/2 розподілу Стьюдента з n-1 ступенями волі;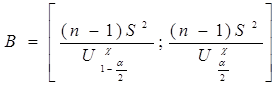 ,
,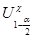 - квантиль рівня 1-a/2 розподілу c2 з n-1 ступенями волі.
- квантиль рівня 1-a/2 розподілу c2 з n-1 ступенями волі.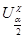
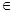 N(μ, s)), якщо її щільність розподілу
N(μ, s)), якщо її щільність розподілу 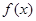 визначається за формулою:
визначається за формулою: ,
, Графік щільності розподілу випадкової величини x має дзвіноподібну форму і є симетричним відносно прямої х= μ (див. рис.8.1)
Графік щільності розподілу випадкової величини x має дзвіноподібну форму і є симетричним відносно прямої х= μ (див. рис.8.1)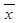 та вибіркове середнє квадратичне відхилення s, отримані за згрупованою вибіркою (див. лаб. роботу № 4).
та вибіркове середнє квадратичне відхилення s, отримані за згрупованою вибіркою (див. лаб. роботу № 4).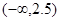 немає вибіркових значень. Тому спочатку необхідно розглянути інтервал
немає вибіркових значень. Тому спочатку необхідно розглянути інтервал 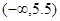 .
. і розглянемо інтервал
і розглянемо інтервал  . У цей інтервал попадає 5 вибіркових значень, що також нас не влаштовує. Якщо розглянемо інтервал
. У цей інтервал попадає 5 вибіркових значень, що також нас не влаштовує. Якщо розглянемо інтервал 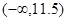 , то одержимо в ньому 8.5 вибіркових значень. Таким чином, перша точка нового групування b1=11.5. Наступним буде інтервал
, то одержимо в ньому 8.5 вибіркових значень. Таким чином, перша точка нового групування b1=11.5. Наступним буде інтервал  , який містить 10.5 значеньі за b2 беремо значення 17.5. Продовжуючи аналогічним чином, одержуємо вторинне групування (див. табл.. 8.2).
, який містить 10.5 значеньі за b2 беремо значення 17.5. Продовжуючи аналогічним чином, одержуємо вторинне групування (див. табл.. 8.2).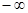
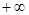
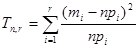 ,
,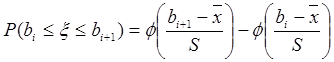 ,
,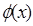 - це інтеграл імовірностей:
- це інтеграл імовірностей: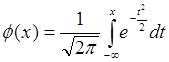 .
.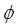 можна використовувати функцію
можна використовувати функцію  ψ:
ψ: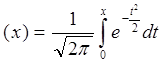 .
.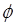 :
: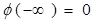 ,
, 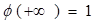 ,
,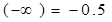 , ψ
, ψ  .
.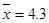 ; S=9.71; n=200 і яка задається таблицею:
; S=9.71; n=200 і яка задається таблицею: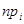
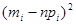
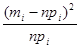
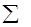

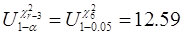 (див. додаток. № 4 до методичних вказівок).
(див. додаток. № 4 до методичних вказівок).