
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод максимальної правдоподібності.ПрикладСодержание книги Поиск на нашем сайте
Розв’язок
Приклад:
Приклад:
1)Нехай 2) 3)
Властивості оцінок макс правдоподібності 1)Якщо, для параметра
2)Нехай
Асимптотична нормальність оцінок максимальної правдоподібності. Нехай Теорема Фішера.
1) 2) 3)
Доведення.
Надійні інтервали. Побудова асимптотичних надійних інтервалів. Приклад. Надійні інтервали:
Асимптотично найкоротший надійний інтервал Нехай
Значення
Нехайn=100, x=40,
Надійні інтервали для параметрів нормального розподілу у випадку, коли один з параметрів відомий.
1.
2. а – відоме,
n – кількість спостережень,
Теорема про незалежність вибіркових середнього та дисперсій для нормального розподілу. Лема1. Нехай Нехай є матриця С n*n. Ця матриця ортогональна Тоді Доведення. Характеристичні функції
Оскільки Лема2.
Доведення.
- Не залежить від Теорема. Нехай вип..вел. Доведення. Доведемо для N(0,1).
Побуд. Надійні інтервали для параметрів нормального розподілу у випадку, коли обидва параметри невідомі. Лемма 1:
Розглянемо ортогональну матрицю
Для
Лемма 2
Теорема Фішера: Нехай
Тоді:
Доведемо для а=0,
Розглянемо матриці виду:
Отже, 3) Отже, третій випадок:
4) Отже, четвертий випадок:
25.Критерій X2
Теорема:
Якщо недіагональні вектори не =0, то компоненти залежні:
Отже,
Побудова критерію: 1)Наперед задається α. 2)За допомогою таблиць визначається значення величини 3) Якщо Зауваження: Якщо функція розподілу містить невідомий параметр, то замість параметра підставляємо оцінки: 26.Критерій Xдля перевірки незалежності та однорідності. Критерій однорідності Цей критерій можна використовувати для перевірки даних, що мають дискретну структуру. Окрім того,за допомогою цього критерію можна перевіряти однорідність будь-якого скінченного числа вибірок. Нехай проведено kпослідовних серій незалежних спостережень, які складаються з
У таблиці Критерій незалежності Критерій
де vij — число випадків, коли одночасно спостерігалися x = xi та h = yj (для неперервних випадкових величин i та j — номери відповідних інтервалів),
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.8 (0.006 с.) |


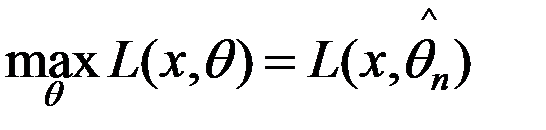 ,
,  -оцінка макс. правдоподібності
-оцінка макс. правдоподібності
 -рівняння правдоподібності
-рівняння правдоподібності
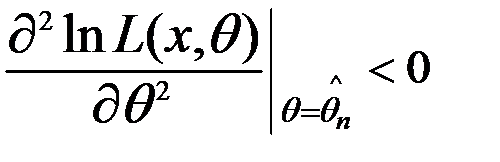 ,
,  -точка max.
-точка max. ;
; 
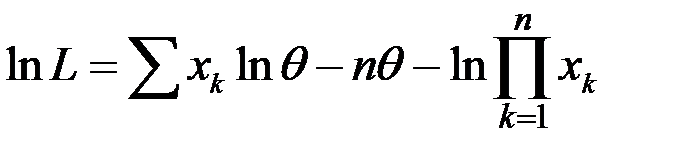 ;
; 
 ;
;  ,
,  -точка max.
-точка max.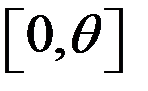
 ;
; 
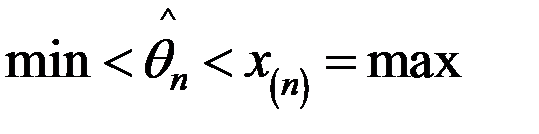 ;
; 
 ;
; 

 ;
; 
 -оцінка max
-оцінка max 
 існує достатня статистика, то оцінки МП-ф-ія достат. статистики.
існує достатня статистика, то оцінки МП-ф-ія достат. статистики. - дост.;
- дост.; 
 ;
; 

 - скаляр.параметр. Якщо, для параметра
- скаляр.параметр. Якщо, для параметра  існує ефектив. оцінки, то вона співпадає з оцінками МП.
існує ефектив. оцінки, то вона співпадає з оцінками МП.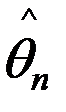 -ефектив.;
-ефектив.;  ;
;  ,
,  - оцінка макс. МП.
- оцінка макс. МП. , де
, де 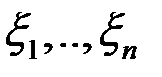 - незалежні однаково розподілені випадкові величини з щільністю
- незалежні однаково розподілені випадкові величини з щільністю  . Тоді
. Тоді 
 незміщена оцінка максимальної правдоподібності,
незміщена оцінка максимальної правдоподібності,  і виконані умови:
і виконані умови: тричі диференційована по
тричі диференційована по  ;
; ;
; ;
;
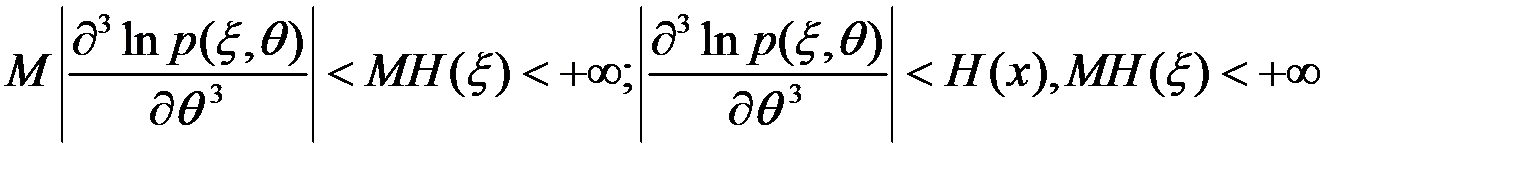 , тоді послідовність оцінок максимальної правдоподібності
, тоді послідовність оцінок максимальної правдоподібності 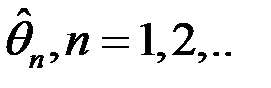 сильно спроможна асимптотична нормальна і асимптотично ефективна, тобто
сильно спроможна асимптотична нормальна і асимптотично ефективна, тобто  - асимптотична ефективність.
- асимптотична ефективність.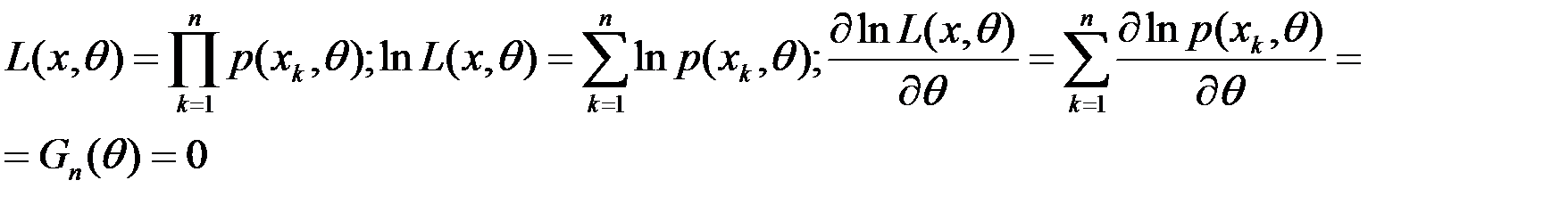 - рівняння правдоподібності.
- рівняння правдоподібності. 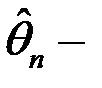 оцінка правдоподібності,
оцінка правдоподібності,  .
.  - істинне значення параметра.
- істинне значення параметра.

 - вип. вел.
- вип. вел. 


 – надійним інтервалом для θ наз. такий інтервал
– надійним інтервалом для θ наз. такий інтервал  , що
, що
 - наперед задана ймовірність
- наперед задана ймовірність
 - деякі функції від вибірки
- деякі функції від вибірки ,
, 
 - оцінка методу максимальної правдоподібності
- оцінка методу максимальної правдоподібності

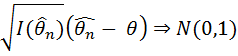
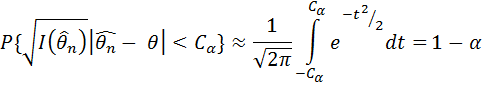
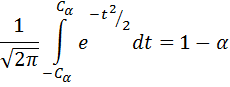



 розв’яжемо цю нерівність відносно
розв’яжемо цю нерівність відносно 

 асимпт. найкор. інтервал
асимпт. найкор. інтервал Пуассонівський розподіл:
Пуассонівський розподіл: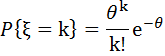

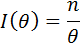


 Біноміальний розподіл:
Біноміальний розподіл: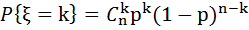









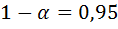


 ,
, - відомий,
- відомий,  - найкраща оцінка парам а, а – невід;
- найкраща оцінка парам а, а – невід;


 - невідомий.
- невідомий.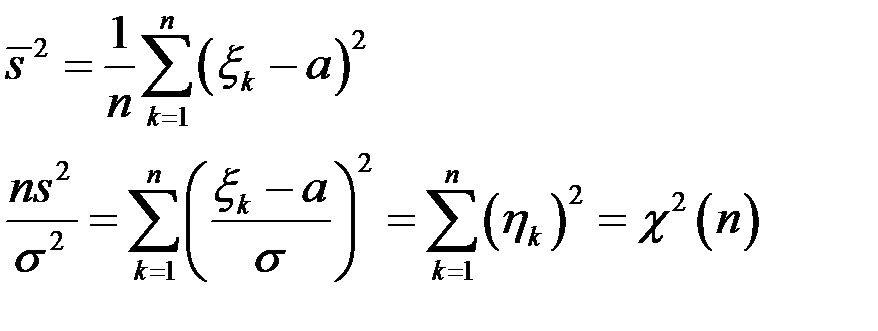




 розподіл з n ступенями волі.
розподіл з n ступенями волі.

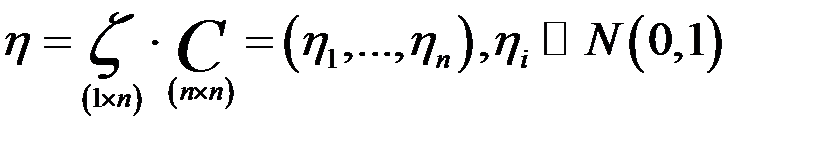
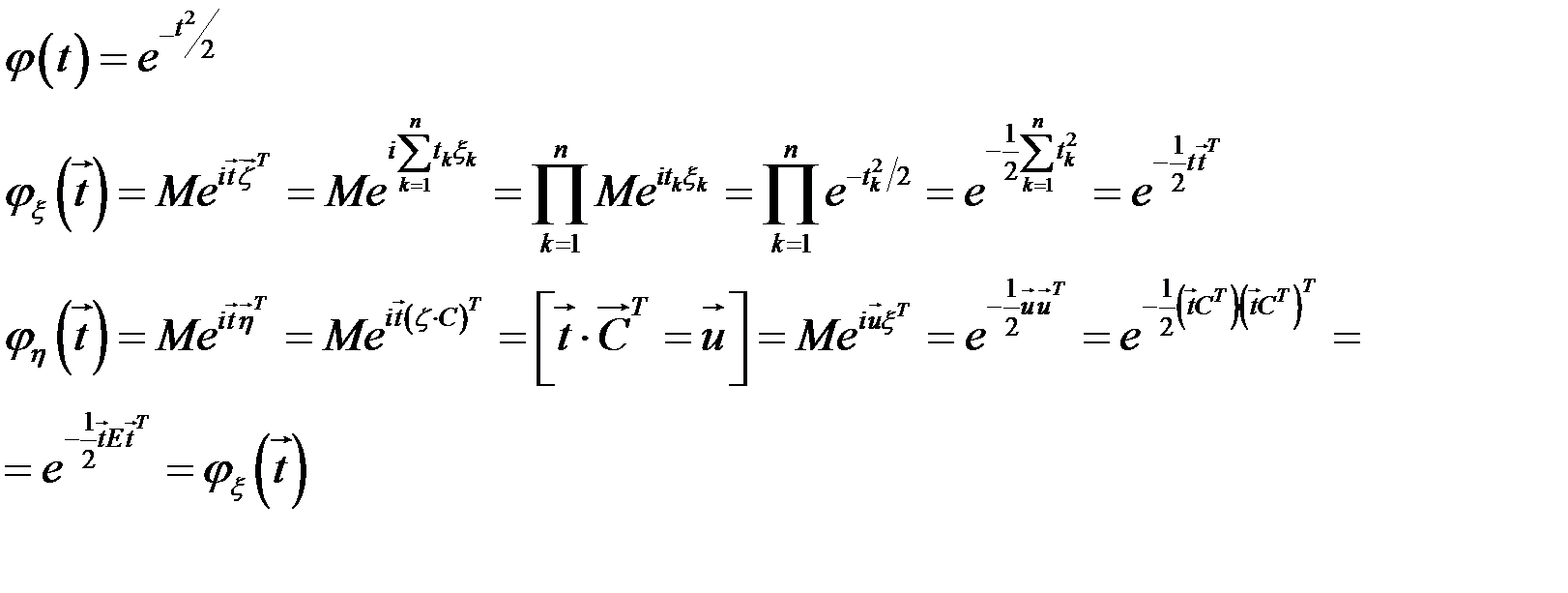
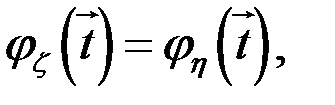 то вони ідентичні.
то вони ідентичні.
 і ця величина не залежить від виразу
і ця величина не залежить від виразу 


 .
.  - векторн.спостер., то статистики
- векторн.спостер., то статистики  незалежні між собою, а
незалежні між собою, а 



 ,
, 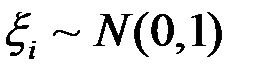
 .
. ,
, 
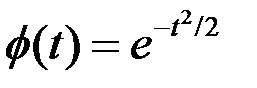


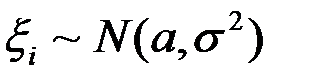 доведення аналогічне.
доведення аналогічне.
 , r<nі
, r<nі 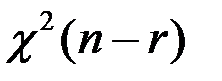 не залежить від
не залежить від  .
.




 і
і 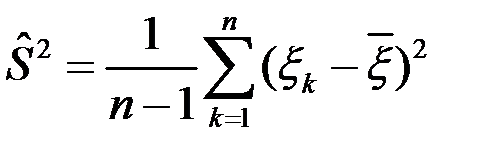 незалежні між собою.
незалежні між собою.




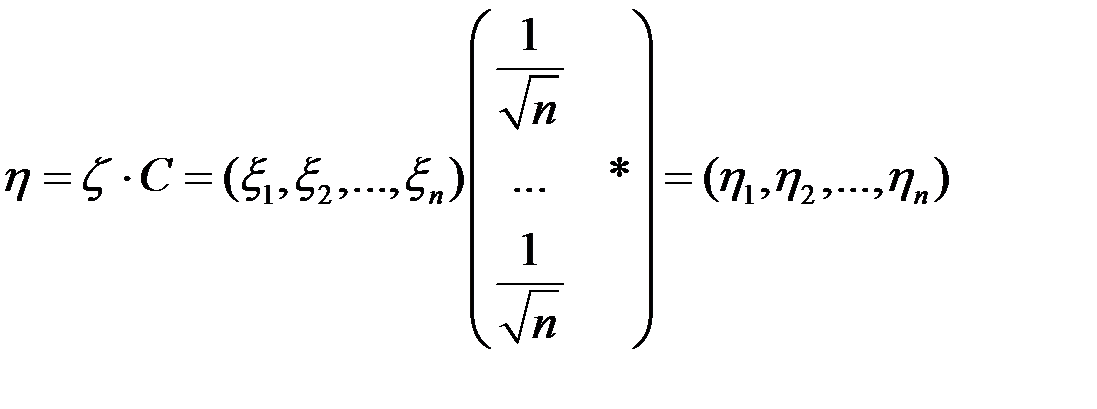

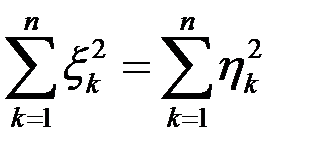

 не залежить від
не залежить від  .
. -невідомі. а-?
-невідомі. а-?



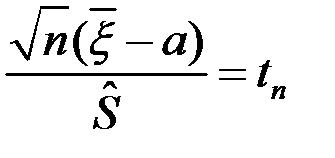


 -невідомі.
-невідомі.  -?
-?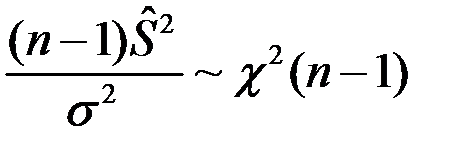






 . Доведення:
. Доведення:





 Доведено.
Доведено.
 і
і 


 спостережень. При цьому в кожному експерименті може виникнути один з
спостережень. При цьому в кожному експерименті може виникнути один з  наслідків, n ij— число виникнень i -го наслідку в j -й серії.
наслідків, n ij— число виникнень i -го наслідку в j -й серії. 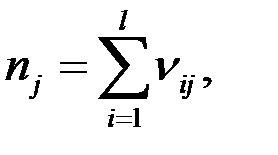
 — загальна кількість об’єм спостережень. Потрібно перевірити гіпотезу H 0 про те, що всі спостереження проводилися над однією і тією ж величиною. Статистикою критерію є величина:
— загальна кількість об’єм спостережень. Потрібно перевірити гіпотезу H 0 про те, що всі спостереження проводилися над однією і тією ж величиною. Статистикою критерію є величина:
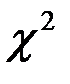 - розподілу за даними
- розподілу за даними  і числом степенів свободи m=(l-1)(k-1) знаходимо число
і числом степенів свободи m=(l-1)(k-1) знаходимо число  . Якщо
. Якщо 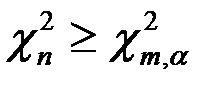 то гіпотеза
то гіпотеза  відхиляється, якщо ж
відхиляється, якщо ж  то гіпотеза приймається.
то гіпотеза приймається.
 дає змогу перевіряти також гіпотезу про незалежність двох випадкових величин
дає змогу перевіряти також гіпотезу про незалежність двох випадкових величин  та h. Статистикою критерію є величина
та h. Статистикою критерію є величина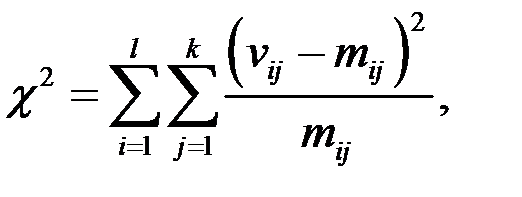

 і
і 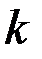 — число значень, яких набувають випадкові величини
— число значень, яких набувають випадкові величини  та h;
та h;  — обсяг вибірки. Вибір табличного значення
— обсяг вибірки. Вибір табличного значення  і прийняття рішення проводиться аналогічно описаній вище процедурі для критерію однорідності
і прийняття рішення проводиться аналогічно описаній вище процедурі для критерію однорідності


