
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ланцюги Маркова з неперервним часом.Содержание книги Поиск на нашем сайте
Ланцюги Маркова з неперервним часом.
Формула Чеклана-Колмогорова
Інфінітизимальні характеристики 1.
1. 2. 3.

Система диференційних рівнянь Колмогорова
Пряма система
Ергодичний розподіл:
Приклад – ланцюги Маркова з неперервним часом
Процеси загибелі та народження
Застосування ланцюгів Маркова в теорії масового обслуговування. Система масового обслуговування(СМО): є n приладів, на які поступають замовлення через випадковий проміжок часу; час обслуговування – випадковий;можливо: всі зайняті; n+1 створюють чергу; т місць у черзі.
якщо параметр т пропущений, то черга М|M|n|m – марківський (описується процесом смертності-народження) М|M|n – с-ма без втрат (М|M|n|0 – формула Ерланта) М|M|1 – 1 прилад, нескінченна черга; параметри
Загрузка системи Якщо
Середня довжина черги М|M|n Ергодичний розподіл – Загрузка системи – М|M|1|0
М|M|n|m
5. Умовні математичні сподівання. Властивості. Мартингали. Приклади. Умовні мат. сподівання:
Формула повної ймов. для умовного мат. сподівання:
Приклад:
Існує
Означення: умовним мат. сподіванням по сігма-алгебріназ.
Властивості умовного мат. сподівання: 1)
2) якщо
3)
4) лінійність
5)
6) 7) якщо
Мартингали: Є послідовність вип. вел
Пара
Приклад1: Нехай
Послідовність
Приклад2:
Приклад3:
Теорема про збіжність Дуба: якщо
Поняття про стохастичні інтеграл Іто. Стохаст диференціал.
w(t) – стандартний вінерівський процес, такий, що він
Властивості інтеграла Іто: 1.
2. 3.
5.
6. w1, w2– незалежні, f,g є M2[a,b]
Загальна f(t) є M2 [a,b] – інтегрована в квадраті.
Стохастичний диференціал. a(t), b(t) – випадкові величини. [ t0, T]
Стохастичнийдифер.вінерівськогопроцесу
Формула Іто:
Стаціонарні процеси. Приклади. Формула Блека-Шоуза. Нехай S(t) - ціна акцій в момент часу t, це випадковий процес, для якого справедливо:
Вип.процес
Вип.процес
Будь-який процес у вузьк. розумінні є і в широкому. R(t) – корел.функція стаціонарного в широкому розум.процесу
Теорема Бохнера-Хінчина
Теорема Хінчина. Неперервна ф-ія
Доведення. Необх.
Дост.
Приклади.
Спектральна функція і спектральна щільність стаціонарного процесу. Теорема Бахнера – Хінчена
Теорема Хінчена
Доведення
Якщо існує
9.Основні задачі математичної статистики: 1) Оцінка невідомих параметрів. Нехай є n-вимірна ( 2) Перевірка статистичних гіпотез.
Основні види: а) гіпотези про розподіл
б) гіпотези однорідності: Нехай є розподіли
в) гіпотези незалежності:
Основні позначення мат. статистики: Нехай є розподіл
В свою чергу, Перепозначимо індекси:
Таким чином утворимо реалізацію варіаційного статистичного ряду.
Гістограма Дискретний статистичний розподіл вибірки можна зобразити графічно у вигляді ламаної лінії, відрізки якої сполучають координати точок (xi; ni), або (xi; Wi). У першому випадку ламану лінію називають полігоном частот, у другому — полігоном відносних частот.
Гістограма частот та відносних частот. Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і висотy Гістограма відносних частот є фігурою, що складається з прямокутників, кожний з яких має основу завдовжки h і висоту, що дорівнює
Площа гістограми частот Площа гістограми відносних частот
Порядкові статистики.
Теорема:
Мода та медіана. Медіана Величина
Оцінка медіани Ме 1) Для дискретних статистичних рядів:
2) Для інтервальних статистичних рядів:
n=36
Мода — найбільш популярне число вибірки. 1) Для дискретного статистичного ряду:
2) Для інтервального статистичного ряду:
Метод моментів. Приклад.
Складемо систему рівнянь:
Якщо можна розв’язати, то є оцінка. Приклад.
Оцінки методу моментів спроможні, асимптотично нормальні, але дуже часто зміщені та неефективні.
Лемма 2
Теорема Фішера: Нехай
Тоді:
Доведемо для а=0,
Розглянемо матриці виду:
Отже, 3) Отже, третій випадок:
4) Отже, четвертий випадок:
25.Критерій X2
Теорема:
Якщо недіагональні вектори не =0, то компоненти залежні:
Отже,
Побудова критерію: 1)Наперед задається α. 2)За допомогою таблиць визначається значення величини 3) Якщо Зауваження: Якщо функція розподілу містить невідомий параметр, то замість параметра підставляємо оцінки: 26.Критерій Xдля перевірки незалежності та однорідності. Критерій однорідності Цей критерій можна використовувати для перевірки даних, що мають дискретну структуру. Окрім того,за допомогою цього критерію можна перевіряти однорідність будь-якого скінченного числа вибірок. Нехай проведено kпослідовних серій незалежних спостережень, які складаються з
У таблиці Критерій незалежності Критерій
де vij — число випадків, коли одночасно спостерігалися x = xi та h = yj (для неперервних випадкових величин i та j — номери відповідних інтервалів),
Критерій Вальда
Ланцюги Маркова з неперервним часом.
Формула Чеклана-Колмогорова
Інфінітизимальні характеристики 1.
1. 2. 3.

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.01 с.) |


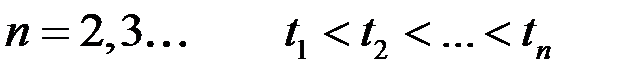

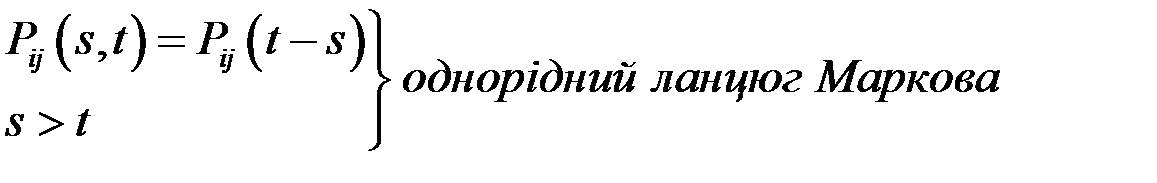

 2.
2. 


 поглинаючий стан
поглинаючий стан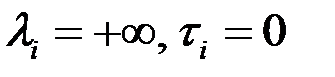 миттєвий стан
миттєвий стан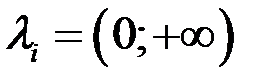 затримуючий стан
затримуючий стан




 регулярний ЛМ
регулярний ЛМ

 - обернена система
- обернена система
 при множенні на попереднє отримуємо наступну систему:
при множенні на попереднє отримуємо наступну систему: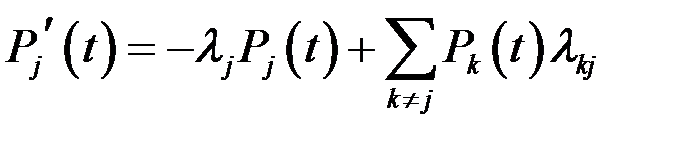



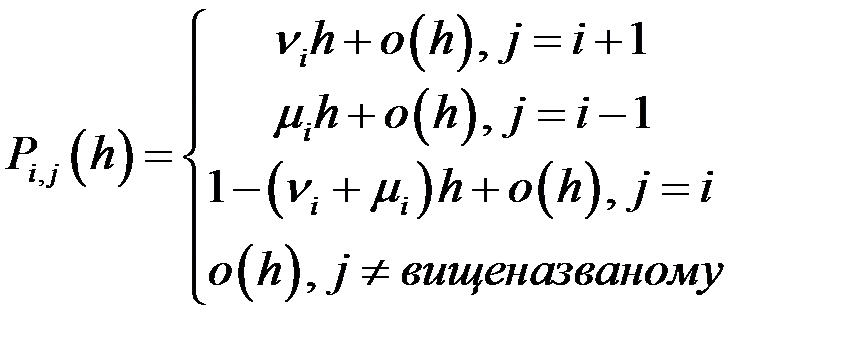
 - інтенс. народження,
- інтенс. народження,  - смерті
- смерті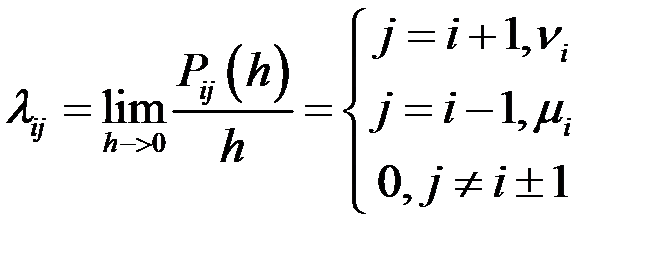

 ,
, 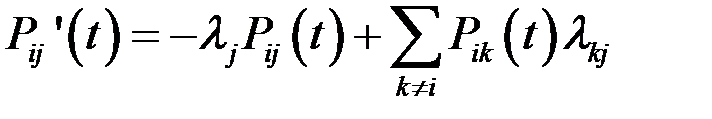
 ,
, 
 ,
, 
 ,
,  ,
, 
 ,
, 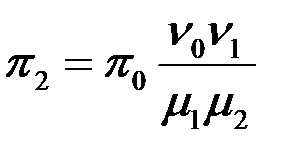
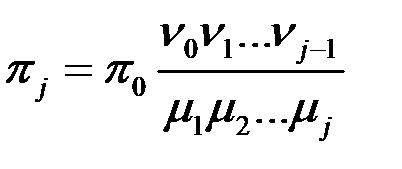 - ймовірність знаходж. в стані j
- ймовірність знаходж. в стані j (умова ергодичності)
(умова ергодичності) A|B|n|m – СМО; A – вхідний потік замовлення, B – відповідає за обслуговування; n- к-сть приладів; m – к-сть місць у черзі,
A|B|n|m – СМО; A – вхідний потік замовлення, B – відповідає за обслуговування; n- к-сть приладів; m – к-сть місць у черзі,


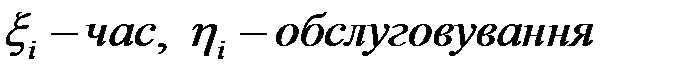 .
.


 ;
; 
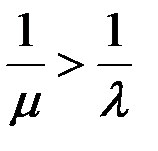 – ергодичний розподіл,
– ергодичний розподіл,  – не ерг. розп., черга росте
– не ерг. розп., черга росте – середнє число замовлень в с-мі
– середнє число замовлень в с-мі



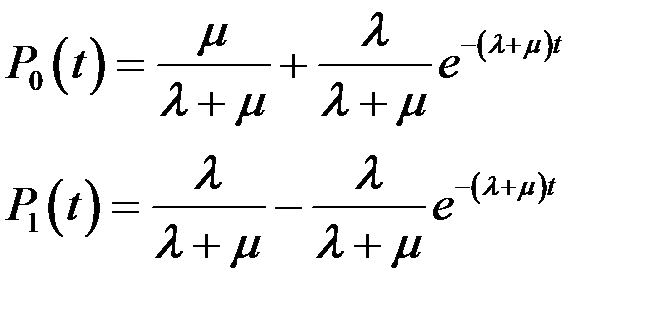
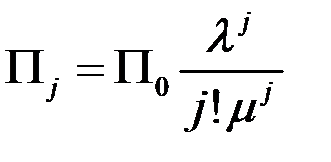 ,
, 

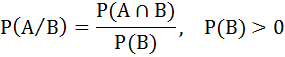
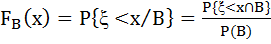 - умовна функція розподілу
- умовна функція розподілу
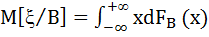 - умовне мат. сподівання
- умовне мат. сподівання





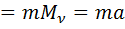
 – ймов. простір
– ймов. простір

 -вимірна вип. вел.
-вимірна вип. вел. 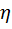 для якої викон. рівність:
для якої викон. рівність: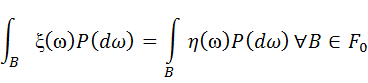



 не залежить від
не залежить від 
 –вимірна
–вимірна
 -
- 






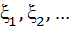

 наз. мартингалом, якщо
наз. мартингалом, якщо 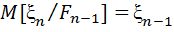 ,
,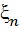 -
-  – субмартингал
– субмартингал - супермартингал
- супермартингал - н.в.в.
- н.в.в.
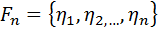

 ,
, 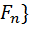 - мартингал
- мартингал



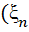 ,
,  - мартингал
- мартингал





 - субмартингал,
- субмартингал, , тоді
, тоді  ,
, 


 - вимірний.
- вимірний. =
= 
 Вводиться функція f(t)
Вводиться функція f(t)  -вимірна,
-вимірна, 
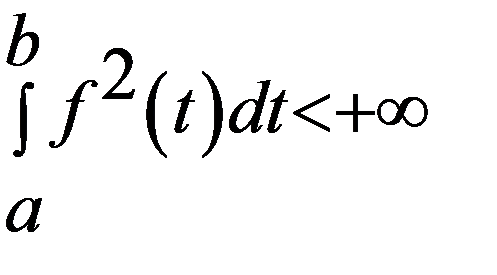 f(t) – ступінчата
f(t) – ступінчата


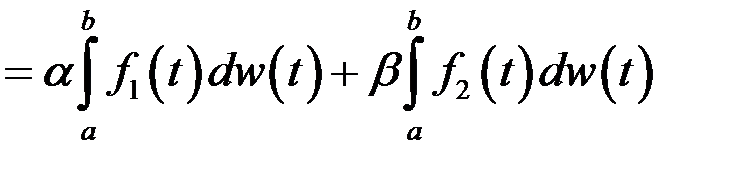







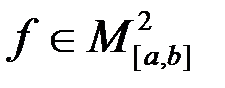
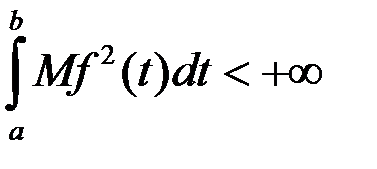


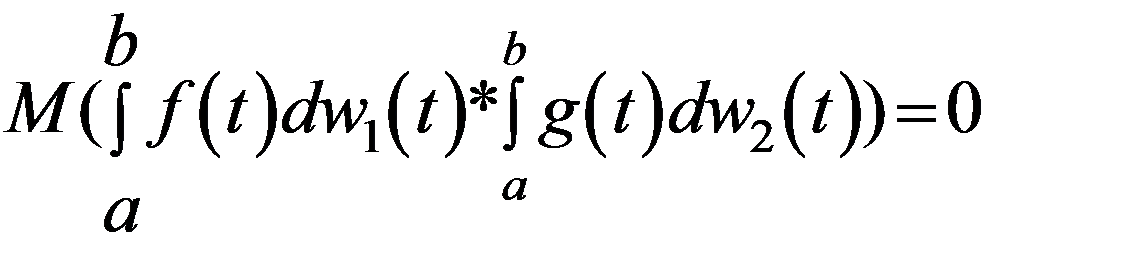




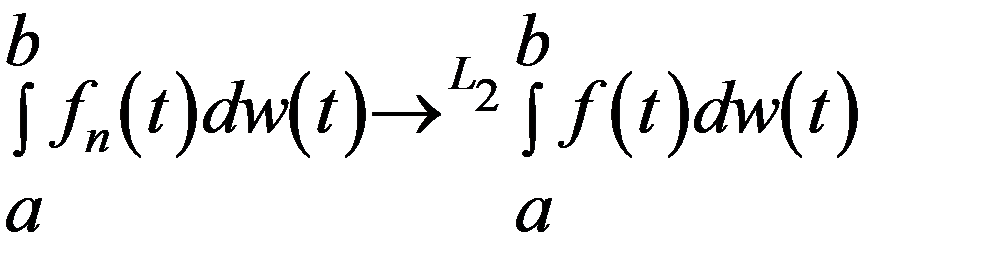 - інтеграл Іто в загал. випадку
- інтеграл Іто в загал. випадку







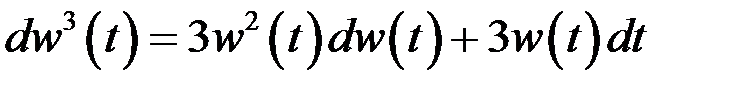
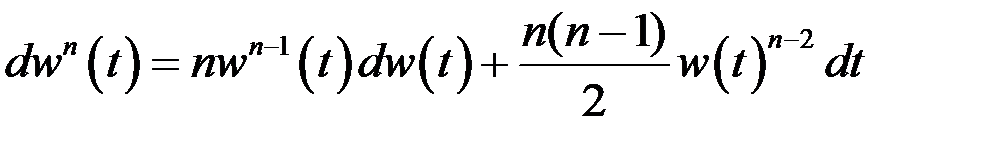



 наз.стаціонарним у вузькому розумінні, якщо
наз.стаціонарним у вузькому розумінні, якщо  розподіл вектора
розподіл вектора  не залежить від
не залежить від  .
.
 наз. стаціонарним в широкому розумінні, якщо
наз. стаціонарним в широкому розумінні, якщо

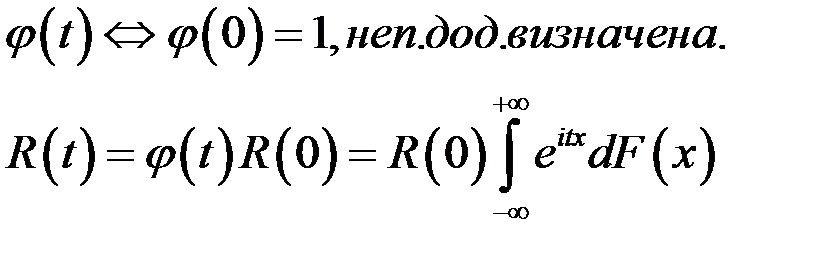





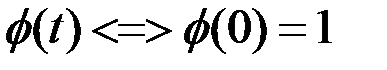

 - корел
- корел 
 - неспаднаф-ція обмеж. варіації
- неспаднаф-ція обмеж. варіації
 - корел
- корел 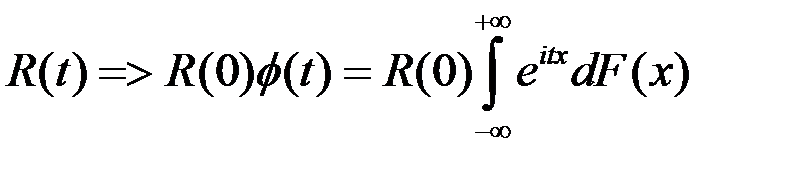

 - спектральна функція
- спектральна функція - спектральна щільність
- спектральна щільність

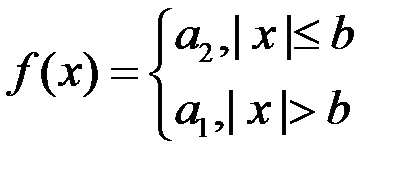
 - корел. ф-я
- корел. ф-я функція розподілу випадкової величини
функція розподілу випадкової величини  Параметр
Параметр  невідомий. Необхідно знайти найкращу оцінку
невідомий. Необхідно знайти найкращу оцінку  .
. - основна гіпотеза
- основна гіпотеза - альтернативна
- альтернативна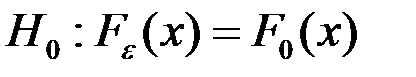

 та
та 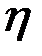

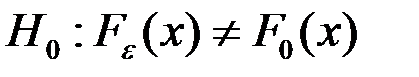
 незалежні
незалежні залежні.
залежні.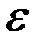 та його функція
та його функція  . Послідовність
. Послідовність  називається вибірка обсягу nз генеральної сукупності випадкової величини
називається вибірка обсягу nз генеральної сукупності випадкової величини 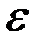 з функції розподілу
з функції розподілу 
 -п.н.о.р.в.в. з
-п.н.о.р.в.в. з 
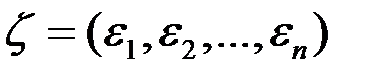
 називається реалізацією вибірки, де
називається реалізацією вибірки, де  - значення
- значення  ,
,  - значення
- значення  ,…,
,…,  - значення
- значення  .
.


 - це є варіаційний статистичний ряд.
- це є варіаційний статистичний ряд. -i-та порядкова статистика.
-i-та порядкова статистика.



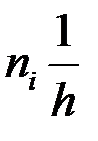 .
. .
.

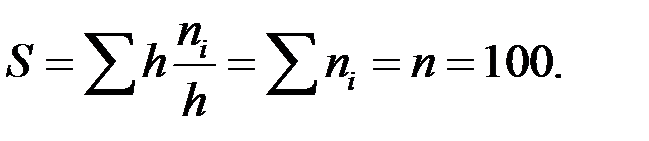
 .
. -k-та порядкова статистика
-k-та порядкова статистика ;
;
 ;
; 



 ;
; 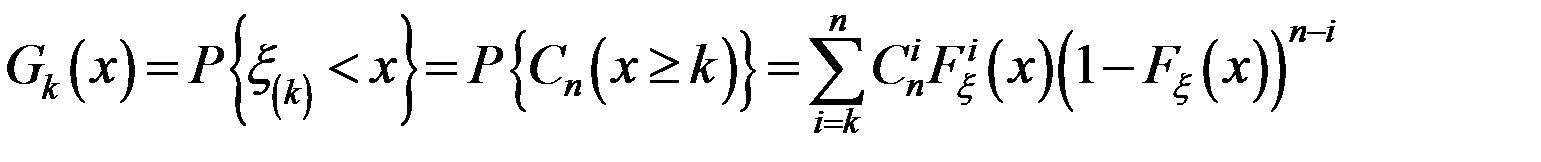

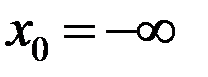 ,
, 

 ;
; 
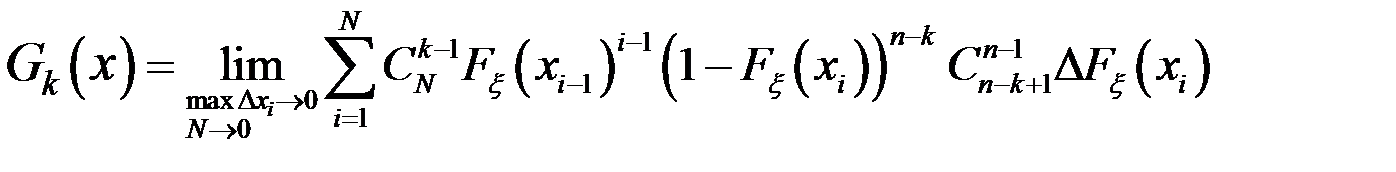


 , k=1,2,…,n+1
, k=1,2,…,n+1 ,
, 


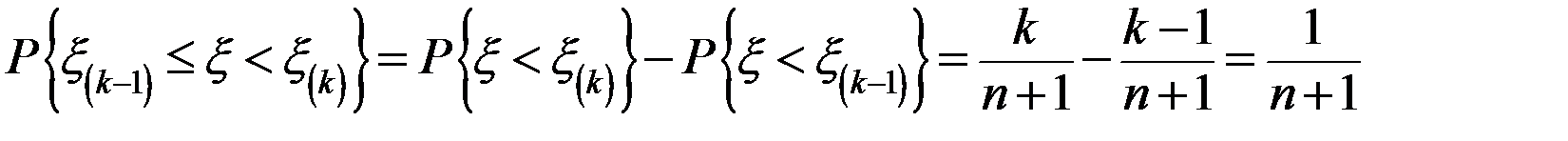
 називається медіаною. для випадкової величини
називається медіаною. для випадкової величини  , якщо
, якщо








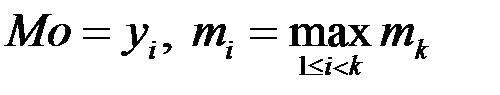






 ,
,





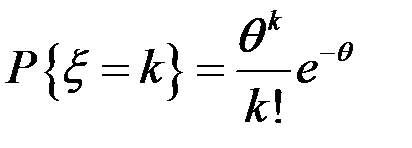


 , r<nі
, r<nі 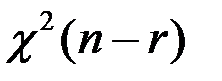 не залежить від
не залежить від  .
.




 і
і 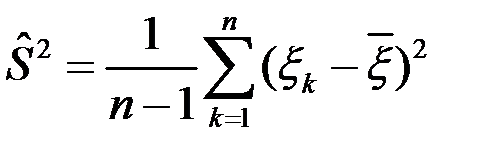 незалежні між собою.
незалежні між собою.




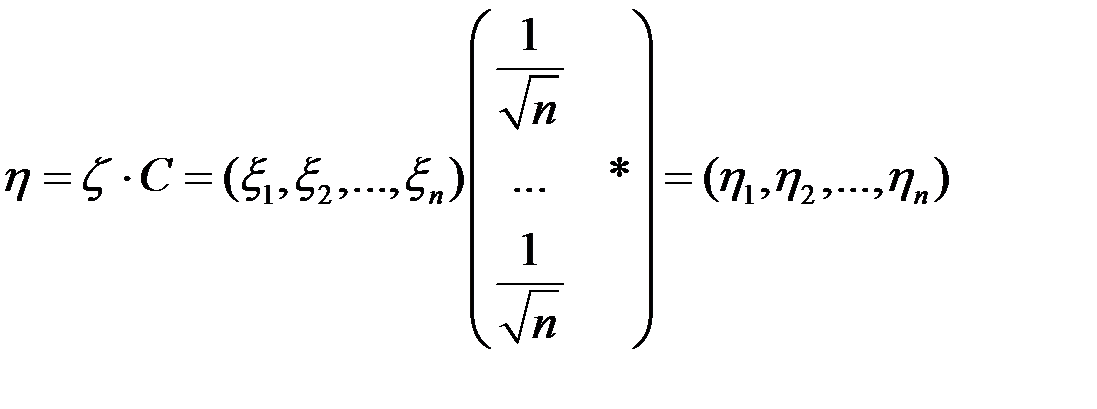

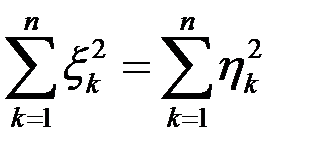

 не залежить від
не залежить від  .
. -невідомі. а-?
-невідомі. а-?



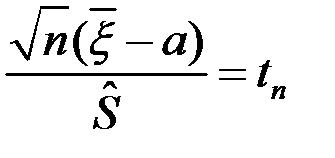


 -невідомі.
-невідомі.  -?
-?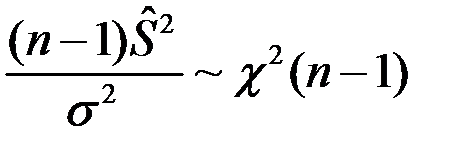






 . Доведення:
. Доведення:





 Доведено.
Доведено.
 і
і 


 спостережень. При цьому в кожному експерименті може виникнути один з
спостережень. При цьому в кожному експерименті може виникнути один з  наслідків, n ij— число виникнень i -го наслідку в j -й серії.
наслідків, n ij— число виникнень i -го наслідку в j -й серії. 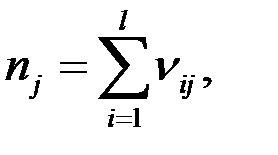
 — загальна кількість об’єм спостережень. Потрібно перевірити гіпотезу H 0 про те, що всі спостереження проводилися над однією і тією ж величиною. Статистикою критерію є величина:
— загальна кількість об’єм спостережень. Потрібно перевірити гіпотезу H 0 про те, що всі спостереження проводилися над однією і тією ж величиною. Статистикою критерію є величина:
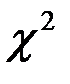 - розподілу за даними
- розподілу за даними  і числом степенів свободи m=(l-1)(k-1) знаходимо число
і числом степенів свободи m=(l-1)(k-1) знаходимо число  . Якщо
. Якщо 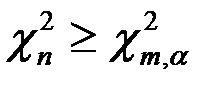 то гіпотеза
то гіпотеза  відхиляється, якщо ж
відхиляється, якщо ж  то гіпотеза приймається.
то гіпотеза приймається.
 дає змогу перевіряти також гіпотезу про незалежність двох випадкових величин
дає змогу перевіряти також гіпотезу про незалежність двох випадкових величин  та h. Статистикою критерію є величина
та h. Статистикою критерію є величина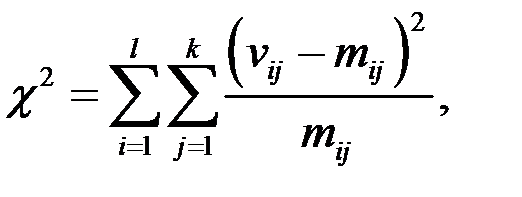

 і
і 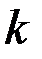 — число значень, яких набувають випадкові величини
— число значень, яких набувають випадкові величини  та h;
та h;  — обсяг вибірки. Вибір табличного значення
— обсяг вибірки. Вибір табличного значення  і прийняття рішення проводиться аналогічно описаній вище процедурі для критерію однорідності
і прийняття рішення проводиться аналогічно описаній вище процедурі для критерію однорідності



