Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибіркові математичне сподівання та дисперсія.Содержание книги Поиск на нашем сайте Нехай Вибірковим моментом k- го порядку називають статистику При k =1 величину Якщо Через При k =2 величину Якщо Зауважимо, що Тут використовувалась рівність Якщо математичне сподівання При дослідженні властивостей графіка щільності розподілу неперервної випадкової величини часто розглядають такі характеристики як коефіцієнти асиметрії Якщо графік щільності розподілу симетричний відносно математичного сподівання, то Аналогічно, для нормального розподілу Мода та медіана. Медіана Величина
Оцінка медіани Ме 1) Для дискретних статистичних рядів:
2) Для інтервальних статистичних рядів:
n=36
Мода — найбільш популярне число вибірки. 1) Для дискретного статистичного ряду:
2) Для інтервального статистичного ряду:
Оцінювання невідомих параметрів по емпіричній функції розподілу. Властивості оцінок.
Класиф.1:оцінка Якщо Класиф.2:незміщена оцінка Класиф.3: незміщена оцінка Класиф.4:незміщена оцінка Оцінка невідомого мат.сподівання: 1.
Властивості оцінок: К.1) К.2) К.3) К.4) Для більшості класичних розподілів вона буде оптимальною
Ефективні точкові оцінки. НерівністьКрамера-Рао
Нехай
Лема 1. Якщо виконуютьсянаступніумови: 1) 2) 3)
НерівністьКрамера-Рао: Нехай Якщовиконуєтьсяумови не лише 1, а також
Наслідок: 1). Нехай
Якщодисперсія незалежної оцінки дорівнює
2). Нехай
Теорема: Незм.оцінка
17. Достатні статистики. Статистика, яка несе в собі всю інформацію про невідомий параметр ϴ наз. достатньою.
Т1. Критерій факторизації Статистика
Доведення Необх-ть:
Достат-ть: Нехай виконується
Приклад: Розподіл Пуасона:

Властивості достатніх статистик Т2. Якщо для ϴ існує оптимальна оцінка, то вона є функцією від достатньої статистики.
Метод моментів. Приклад.
Складемо систему рівнянь:
Якщо можна розв’язати, то є оцінка. Приклад.
Оцінки методу моментів спроможні, асимптотично нормальні, але дуже часто зміщені та неефективні.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 698; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 - k- й момент випадкової величини, тобто
- k- й момент випадкової величини, тобто  .
. .
. наз. вибірковим середнім і позначають
наз. вибірковим середнім і позначають  .
. - реалізація вибірки
- реалізація вибірки  , то через
, то через  будемо позначати середнє арифметичне
будемо позначати середнє арифметичне 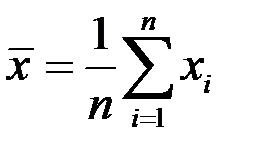 , а через
, а через  .
. . Аналогічно, вибірковим центральним моментом k- го порядку називають випадкову величину
. Аналогічно, вибірковим центральним моментом k- го порядку називають випадкову величину  .
. називають вибіркову дисперсією і позначають символом
називають вибіркову дисперсією і позначають символом  .
. , то
, то  являються незміщеною, сильно спроможною, а якщо
являються незміщеною, сильно спроможною, а якщо  , то асимптотично нормальною оцінкою математичного сподівання
, то асимптотично нормальною оцінкою математичного сподівання  (у цьому випадку
(у цьому випадку  ).
). . Перевіримо, чи буде незміщеною оцінка
. Перевіримо, чи буде незміщеною оцінка  дисперсії:
дисперсії: 
 . Отже,
. Отже,  є незміщеною оцінкою дисперсії. Нехай
є незміщеною оцінкою дисперсії. Нехай  , тоді
, тоді  . Тобто
. Тобто  є незміщеною оцінкою дисперсії. При цьому вона буде і сильно спроможною оцінкою.
є незміщеною оцінкою дисперсії. При цьому вона буде і сильно спроможною оцінкою. відоме, то незміщеною, сильно спроможною і асимптотично нормальною оцінкою дисперсії є оцінка
відоме, то незміщеною, сильно спроможною і асимптотично нормальною оцінкою дисперсії є оцінка  .
.
 і ексцесу
і ексцесу  :
:  .
. . Наприклад, для нормального розподілу
. Наприклад, для нормального розподілу  . При
. При  симетрія порушена вправо, а при
симетрія порушена вправо, а при  - вліво.
- вліво. . Якщо для деякого розподілу
. Якщо для деякого розподілу  , то кажуть, що він має нормальний ексцес. При
, то кажуть, що він має нормальний ексцес. При  , вважають,що ексцес додатній(від’ємний). Відповідні вибіркові коефіцієнти асиметрії та ексцесу визначаються по формулам:
, вважають,що ексцес додатній(від’ємний). Відповідні вибіркові коефіцієнти асиметрії та ексцесу визначаються по формулам:  .
. називається медіаною. для випадкової величини
називається медіаною. для випадкової величини  , якщо
, якщо








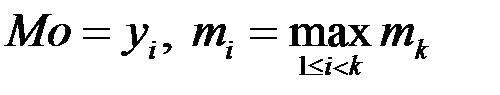






 ,
,


 , x=
, x=  )
) , Оцінка
, Оцінка  . Будь-яка функція від вибірки - статистика.
. Будь-яка функція від вибірки - статистика. невідомого параметра
невідомого параметра  наз. незміщеною,якщо
наз. незміщеною,якщо 
 - оц. зміщенна.
- оц. зміщенна.  - зсув оцінки.
- зсув оцінки. невід.параметра
невід.параметра  назив. спроможною, якщо
назив. спроможною, якщо 
 невід.параметра
невід.параметра  назив. асимптотично нормальною,якщо
назив. асимптотично нормальною,якщо 
 назив. оптимальною,якщо дисперсія найменша серед усіх можливих оцінок.
назив. оптимальною,якщо дисперсія найменша серед усіх можливих оцінок.

 - найкраща оцінка
- найкраща оцінка
 =
= 



 - вибіркове середнє
- вибіркове середнє




 - функціяправдоподібності
- функціяправдоподібності

 , тоді
, тоді

 - щільн.
- щільн. 
 - довільнанезалежнаоцінкафукції
- довільнанезалежнаоцінкафукції 
 - двічі непер.дифер., дисперсія оцінки обмежен. та
- двічі непер.дифер., дисперсія оцінки обмежен. та 
 , де
, де 

 - незалежна оцінка для a
- незалежна оцінка для a
 , то оцінка ефективна. Якщо для
, то оцінка ефективна. Якщо для  існує ефективна оцінка, то вона оптимально.
існує ефективна оцінка, то вона оптимально. ,
, 
 - найкраща оцінка для
- найкраща оцінка для 


 - ефективна оцінка
- ефективна оцінка - зміщена оцінка
- зміщена оцінка , тоді
, тоді 

 ефективнатоді і тількитоді, коли перша похідна:
ефективнатоді і тількитоді, коли перша похідна:

 достатня коли функція правдоподібна, тобто
достатня коли функція правдоподібна, тобто 
 - тривіальна достатня статистика
- тривіальна достатня статистика -достатня статистика,
-достатня статистика,  ,
, 



 - довільна незміщена статистика від ϴ.
- довільна незміщена статистика від ϴ. - нетривіальна достатня статистика
- нетривіальна достатня статистика

 Ф-ія від достат. статистики буде найкр. оцінкою.
Ф-ія від достат. статистики буде найкр. оцінкою.