
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення параметрів розподілу випадкових величин та перевірка гіпотезСодержание книги
Поиск на нашем сайте Статистичні гіпотези - це припущення, котрі відносяться до виду розподілу випадкової величини, або окремих його параметрів. Задача випробування статистичних гіпотез виникає тоді, коли обставини вимушують нас робити вибір між двома способами дії. Для оцінювання параметрів по емпіричним законам формулюється нульова гіпотеза (Н0) про "відсутність розбіжностей". Нульова гіпотеза є прикладом статистичного висновку: якщо нульову гіпотезу відкинути, то висновок полягає в тому, що у сукупності, котра розглядається є розбіжності, тобто приймається альтернативна гіпотеза Н1. Ймовірність з якою може бути відхилена нульова гіпотеза називається рівнем значущості (для медико-біологічних досліджень достатнім є рівень значущості Перевірка гіпотез, як правило, зводиться до перевірки статистичних характеристик, що оцінюють параметри законів розподілу. Для перевірки гіпотез використовують статистичний критерій К - це правило, яке забезпечує прийняття вірності гіпотези і відхилення хибної з великою ймовірністю. Сукупність значень, при яких основна гіпотеза не приймається, називається критичною областю. Точки, що відділяють критичну область від області прийняття рішень називаються критичними. Для визначення критичної області задається рівень значущості Розглянемо приклад. Процес виробництва ліків є складним. Будь-яке відхилення (навіть незначне) від технології спричиняє появу високотоксичної побічної домішки. Токсичність цієї домішки може бути настільки великою, що навіть така її кількість, яка не може бути визначена при хімічному аналізі, є небезпечною для пацієнта. Тому перед тим, як випускати у продаж партію ліків її досліджують на токсичність біологічними методами: невеликі дози препарату вводяться певній кількості тварин і результати реєструються. Кількість тварин, що загинули, є випадковою величиною. Як правило ін'єктується декілька груп тварин. Дослідження препарату може призвести до однієї з двох можливих дій: - випустити партію ліків у продаж; - повернути партію постачальнику для переробки або знищення. Вибір між двома діями може привести до здійснення помилок двох видів: - визнати препарат безпечним для пацієнтів, коли насправді препарат небезпечний. Ця помилка може коштувати життя пацієнта. - визнати препарат небезпечним для пацієнтів, коли насправді він є безпечним. Наслідки цієї помилки можуть бути виражені в додаткових фінансових затратах. Таким чином, наслідки помилок є різними за своїми значеннями, тому при випробуванні гіпотез є важливим уникати однієї із можливих помилок, яка є більш важливіша, ніж інша. Отже, при перевірці гіпотез можливі помилки двох видів: · Н0 відкидається, коли вона правильна - помилка 1-го роду. · Н0 приймається, коли правильна НІ - помилка ІІ- го роду. Понижуючи рівень значущості ми зменшуємо ймовірність помилки першого роду, але при цьому збільшується ймовірність помилки другого роду. Зазначимо, що чим більша міцність критерію, тим менша ймовірність помилки другого роду. Етапи перевірки гіпотез 1. Визначення статистичної моделі, що буде використовуватися. Тут висувають деякий набір передумов відносно закону розподілу випадкової величини і її параметрів. Наприклад, закон розподілу нормальний, величини незалежні і т.д. 2. Формулювання нульової та альтернативної гіпотези Н0 і Н1. 3. Вибирають критерій, котрий підходить до висуненої статистичної моделі. Вибирають рівень значущості 4. Визначають критичну область для перевірки гіпотези Н0. Якщо значення критерію попадає в цю область, то Н0 відкидається. При умові, що Н0 правильна, ймовірність попадання в критичну область дорівнює 5. Розраховують значення вибраного статистичного критерію для існуючих даних. Порівнюють розраховане значення критерію з критичним і потім вирішують прийняти чи відкинути Н0. Критерії перевірки гіпотез Однією з задач математичної статистики є встановлення узгодженості послідовності спостережень випадкових величин або подій з гіпотезами щодо розподілу випадкової величини (або ймовірності події). Гіпотези, що перевіряються, формулюються або на основі теоретичних міркувань, або в процесі статистичного дослідження. Перевірка гіпотез, як правило, зводить до оцінювання параметрів закону розподілу. Твердження, які формулюються, стосуються значень параметрів законів розподілу. З таких тверджень формулюються наслідки. Наслідки мають характер імовірнісних тверджень щодо поведінки статистичних характеристик. Перевірка полягає у обчисленні цих характеристик за даними спостережень. Такі характеристики називаються критеріями перевірки (К). Для критеріїв перевірки заздалегідь фіксують рівень значущості Нехай - якщо - якщо Розглянемо критерії, що найчастіше використовуються при аналізі медико-біологічних даних.
Критерій Нехай в експерименті спостерігається одна з Складемо вираз: Граничний розподіл Сформулюємо критерій - якщо - якщо
В медико-біологічних дослідженнях часто виникає задача оцінювання параметрів розподілу за малими вибірками. Для оцінювання параметрів розподілу таких вибірок використовують розподіл Ст'юдента. Розв'язок рівняння: Сформулюємо критерій Ст'юдента: - якщо - якщо Стійкість критеріїв Будь-які гіпотези перевіряють, висуваючи спочатку комплекс деяких передумов про закон розподілу випадкової величини. Невиконання передумов робить висновки із відповідних перевірок не відповідними істині. У зв'язку з цим, при розв'язанні реальної задачі необхідно підібрати критерії, що підходять для умов саме цієї задачі. Оскільки існує велика кількість різних критеріїв (особливо непараметричних), це може викликати певні труднощі у спеціалістів, для яких статистичні методи є всього лиш інструментом, яким вони користуються рідко. Тому розглянемо певну послідовність дій, притримуючись якої можна зробити правильний вибір.
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

 = 0,05). Рівень значущості задається заздалегідь. Ймовірність прийняття правильності рішення (гіпотеза Н0 є вірною) називається довірчою ймовірністю (для медико-біологічних досліджень р = 0,95).
= 0,05). Рівень значущості задається заздалегідь. Ймовірність прийняття правильності рішення (гіпотеза Н0 є вірною) називається довірчою ймовірністю (для медико-біологічних досліджень р = 0,95).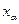 щоб
щоб  .
.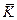 - значення критерію, що розрахований по вибірці:
- значення критерію, що розрахований по вибірці: , то гіпотеза відхиляється;
, то гіпотеза відхиляється; , то гіпотеза приймається.
, то гіпотеза приймається. (критерій Пірсона)
(критерій Пірсона) подій
подій  ;
;  - гіпотетичні ймовірності цих подій. Проведено
- гіпотетичні ймовірності цих подій. Проведено 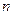 спостережень, при цьому подія
спостережень, при цьому подія  спостерігалась
спостерігалась  к разів,
к разів, 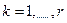

 є
є  ступенями вільності, де
ступенями вільності, де  - число незалежних параметрів розподілу (для нормального закону
- число незалежних параметрів розподілу (для нормального закону 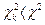 -приймається нульова гіпотеза Н0;
-приймається нульова гіпотеза Н0; -відхиляється нульова гіпотеза і приймається альтернативна гіпотеза.
-відхиляється нульова гіпотеза і приймається альтернативна гіпотеза. -критерій Ст'юдента
-критерій Ст'юдента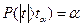 для випадкової величини
для випадкової величини  з табличним
з табличним  .
.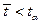 - приймається нульова гіпотеза Но;
- приймається нульова гіпотеза Но;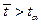 - відхиляється нульова гіпотеза і приймається альтернативна гіпотеза Н1.
- відхиляється нульова гіпотеза і приймається альтернативна гіпотеза Н1.


