
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Медичні та біологічні моделіСодержание книги
Поиск на нашем сайте Кінетичні моделі популяції клітин В основі процесів обміну клітини з середовищем і внутрішнього метаболізму лежить складна мережа організованих певним чином в часі і просторі різних реакцій. В результаті цих процесів змінюються концентрації різних речовин, чисельність окремих кліток, біомаса організмів, можуть змінюватися і інші величини, наприклад величина трансмембранного потенціалу в клітці. Зміни всіх цих величин в часі і складають кінетику біологічних процесів. Основні початкові передумови при описі кінетики в біологічних системах загалом такі ж, як і в хімічній кінетиці. Розглянемо простий приклад замкнутої популяції кліток, в якій одночасно відбуваються процеси розмноження і загибелі і в надлишку є поживні речовини. Виникає питання, як міняється чисельність кліток в такій системі з часом і чи може в ній врешті-решт встановитися стаціонарний стан, коли число кліток мінятися не буде. Це типова кінетична задача, яка розв'язується за допомогою звичайних диференціальних рівнянь. Нехай в деякий момент часу t концентраціякліток в середовищі складе N. Швидкість d N /d t зміниконцентрації кліток у середовищі складається з швидкості їх розмноження Vрозмн і швидкості загибелі Vзагиб:
У простому випадку швидкість розмноження, тобто збільшення концентрації кліток в одиницю часу, пропорційна їх чисельності в кожен момент:
де k 1 – константа пропорційності, що залежить від умов середовища (температура, наявність поживних речовин та ін.). Аналогічно
де k 2 – константа пропорційності, що визначає інтенсивність процесів загибелі кліток. Звідси витікає, що
де Розв’язавши це рівняння, ми знайдемо, як змінюється концентрація клітин в середовищі з часом N = N (t):
де N 0 – концентрація кліток в початковий момент часу t = 0 спостереження за системою. Можна побачити, що в залежності від величин констант швидкостей процесів загибелі k 2 і розмноження k 1 доля цієї популяції буде різною. Якщо Іншим прикладом моделі зростання популяції в середовищі з обмеженою кількістю поживних речовин служить рівняння логістичної кривої. Логістичне рівняння Ферхлюста має вид:
Як видно, динаміку біологічних процесів можна описувати рівняннями, що аналогічні рівнянням хімічної кінетики. Проте, в порівнянні зі звичайною хімічною кінетикою, біологічна кінетика характеризується наступними особливостями: 1. Як змінні виступають не тільки концентрації речовин, але і інші величини. 2. Змінні змінюються не тільки в часі, але і в просторі. 3. Біологічна система просторово гетерогенна, і умови взаємодії реагентів можуть бути різні в різних точках системи. 4. Існують спеціальні механізми саморегуляції, що діють за принципом зворотнього зв'язку. Основна задача в біофізиці складних систем полягає в тому, щоб одержати характеристики різних динамічних режимів і з'ясувати умови і значення параметрів, при яких вони реалізуються в живій клітині. Модель відкритої системи Розглянемо просту відкриту систему, в якій відбувається обмін речовинами "a" і "b" з навколишнім середовищем і, крім того, зворотня реакція першого порядку перетворення Не дивлячись на простоту, модель відображає основні риси обмінних процесів в клітині. Надходження субстрата із зовнішнього середовища задається реакцією A→a, викид метаболітів у зовнішнє середовище задається Рівняння кінетики для цієї системи мають вигляд
Для розв’язку цих рівнянь необхідно задати початкові умови – концентрації речовин у клітині a 0 і b 0 при t = 0. Така відкрита система через певний проміжок часу приходить у стаціонарний стан, в якому змінні а і b приймають постійні значення Виявляється, що величини
На рис.3 наведено декілька видів перехідних кривих а (t). Схожі за формою криві спостерігалися, наприклад, у фізіологічних дослідженнях швидкості дихання за різних початкових умов. Ці випадки отримали спеціальні назви, позначені на мал.3. Навіть з аналізу простої системи (17) і (18) видно, що аналітичні розв’язки мають досить громіздкий вигляд і залежать від великого числа параметрів. Ясно, що при великому числі змінних такі розв’язки не тільки важко отримати, але по них вже і складно з'ясувати залежність кінетичної поведінки системи від параметрів. Звернемо увагу на те, що рівняння (4) містять в правих частинах тільки лінійні члени, куди невідомі змінні входять в першій степені. Проте в біологічних системах процеси, як правило, істотно нелінійні. Так, швидкість простої бімолекулярної реакції другого порядку описується математично у вигляді добутку концентрацій реагентів, тобто в моделі такої реакції праві частини рівнянь містять нелінійні члени. В цьому випадку знаходження точних аналітичних розв’язків стикається із серйозними математичними труднощами а часом взагалі неможливе. Тому основний підхід в сучасній кінетиці і математичному моделюванні біологічних процесів полягає у відмові від знаходження точних аналітичних розв’язків диференціальних рівнянь. Ідея полягає в отриманні якісних характеристик динамічної поведінки системи: стійкі і нестійкі стаціонарні стани, переходи між ними, коливальні режими, якісна залежність поведінки системи від критичних значень параметрів. Найважливішою властивістю стаціонарного стану є його стійкість. Ця стійкість визначається здатністю системи самовільно повертатися в стаціонарний стан після внесення зовнішніх збурень, що відхилюють систему від початкової стаціонарної точки рівноваги. У складній системі можуть протікати реакції другого і вищих порядків. Це відповідає тому, що така система може володіти декількома стаціонарними станами.
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

 . (6)
. (6) , (7)
, (7) , (8)
, (8) , (9)
, (9)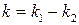 .
. , (10)
, (10) , то
, то  і в системі відбуватиметься необмежене зростання числа кліток з часом:
і в системі відбуватиметься необмежене зростання числа кліток з часом:  , а якщо
, а якщо  , то
, то  ,то з часом популяція вимиратиме:
,то з часом популяція вимиратиме:  . І лише в окремому випадку при
. І лише в окремому випадку при  число кліток залишатиметься постійним:
число кліток залишатиметься постійним:  .
. . (11)
. (11) Тут Nmax – максимальна чисельність популяції, що можлива в даних умовах. Крива N =N (t), щоописується цим рівнянням, має дві характерні ділянки (див. рис.2). У початковий період зростання, коли N < N ma x,крива носить експоненційний характер. Потім, після точки перегину, нахил поступово зменшується і крива наближається до верхньої асимптоти N = Nmax, тобто до максимально досяжного рівня популяції в даних умовах.
Тут Nmax – максимальна чисельність популяції, що можлива в даних умовах. Крива N =N (t), щоописується цим рівнянням, має дві характерні ділянки (див. рис.2). У початковий період зростання, коли N < N ma x,крива носить експоненційний характер. Потім, після точки перегину, нахил поступово зменшується і крива наближається до верхньої асимптоти N = Nmax, тобто до максимально досяжного рівня популяції в даних умовах. (див.рис.3). Позначимо а, b – змінні концентрації усередині системи; А, В – постійні концентрації цих же речовин у зовнішніх резервуарах; kA, kab, kba, kB – константи швидкостей процесів.
(див.рис.3). Позначимо а, b – змінні концентрації усередині системи; А, В – постійні концентрації цих же речовин у зовнішніх резервуарах; kA, kab, kba, kB – константи швидкостей процесів. реакцією b→В, а процесам клітинного метаболізму відповідає перетворення а
реакцією b→В, а процесам клітинного метаболізму відповідає перетворення а  b. Наприклад, для процесу дихання на етапі А→а відбувається надходження глюкози і кисню, етап b→B відповідає викиду СО2 і Н2О з клітини, а весь метаболічний дихальний цикл трансформації молекули глюкози представлений реакцією а
b. Наприклад, для процесу дихання на етапі А→а відбувається надходження глюкози і кисню, етап b→B відповідає викиду СО2 і Н2О з клітини, а весь метаболічний дихальний цикл трансформації молекули глюкози представлений реакцією а  , (12)
, (12) . (12)
. (12) і
і  . Знайти їх можна, прирівнявши до нуля праві частини рівнянь (17) і (18).
. Знайти їх можна, прирівнявши до нуля праві частини рівнянь (17) і (18). У цьому полягає властивість еквіфінальності стаціонарних станів, яка властива відкритим системам і часто спостерігається при вивченні біологічних процесів. Хоча початкові умови не впливають на значення
У цьому полягає властивість еквіфінальності стаціонарних станів, яка властива відкритим системам і часто спостерігається при вивченні біологічних процесів. Хоча початкові умови не впливають на значення 


