
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальний вид представлення частот і їх пропорцій у вибіркових сукупностяхСодержание книги
Поиск на нашем сайте
Примітка:В таблиці 1 крапка замість індексу означає сумування по цьому індексу
Для визначення достовірності відмінності пропорцій Р1 і Р2 (із заданою довірчою імовірністю
де Розраховане критеріальне значення z порівнюється з процентною точкою стандартного нормального розподілу[2] для рівня значущості[3] Крім того, слід зазначити, що включений у формулу (1) вираз є поправкою Іейтса на неперервність. Це пов'язано з тим, що неперервний розподіл (у нашому випадку нормальний) використовується для представлення дискретного розподілу частот. Поправку Іейтса рекомендується застосовувати завжди, оскільки її включення у формулу (1) приводить до точнішої оцінки порівняння імовірності, ніж у разі, коли поправка не використовується. Крім того, можна обчислити досягнутий рівень значущості р [4] (іноді його в літературі називають мінімальним або найменшим) і порівняти його із заданим рівнем значущості
де Побудований на основі виразу (3) інтервал включатиме дійсну різницю пропорцій приблизно в
Приклад Порівняємо частоту виникнення небажаних побічних реакцій в експериментальній і контрольній групах, початкові дані для яких приведені в табл. 2. Поряд з даними в дужках вказані позначення, які відповідають використовуваним у вищенаведених формулах. Для розрахунків скористаємося електронним таблицями MS Excel. Вид початкових даних і отриманих результатів на робочому листі MS Excel приведений в таблиці 3. Відповідно до отриманих результатів можна зробити наступні висновки:
Таблиця 2. Частота виникнення побічних реакцій і їх доля в відповідних групах
1.Оскільки розраховане значення z-критерію (2.5182) більше критичною значення стандартного нормального розподілу при рівні значущості 0,05 (1,96) (за умови, що критерій двосторонній), то нульова гіпотеза відхиляється і приймається альтернативна, яка припускає, що з довірчою вірогідністю 95% пропорції
Таблиця №3. Вихідні дані і результати обчислень за допомогою табличного процесора MS Exel
Р1 і Р2 розрізняються. Іншими словами, можна стверджувати, що імовірність розвитку небажаних побічних явищ/реакцій при лікуванні пацієнтів першим методом статистично значущо менша, ніж при лікуванні другим методом. 2. Величина значення р рівна 0,012 (досягнутий рівень значущості менше заданого рівня значущості 3. Стандартна помилка різниці оцінок пропорцій Р1 і Р2 рівна 0,07. 4. Довірчий інтервал для різниці пропорцій Р1 і Р2, отриманий з використанням виразу (3), має наступний вигляд:
Література
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |







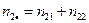





 % можна застосувати z-критерій, критерійне значення якого розраховується по формулі:
% можна застосувати z-критерій, критерійне значення якого розраховується по формулі: (1)
(1) ,
, 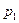 - вибіркова оцінка Р1,.
- вибіркова оцінка Р1,.  - вибіркова оцінка Р2 .
- вибіркова оцінка Р2 . , оскільки даний критерій є двостороннім. Якщо обчислене значення перевищує критичне для заданого рівня значущості, то нульова гіпотеза відхиляється на користь альтернативної, згідно якої пропорції Р1, і Р2 розрізняються з довірчою імовірністю
, оскільки даний критерій є двостороннім. Якщо обчислене значення перевищує критичне для заданого рівня значущості, то нульова гіпотеза відхиляється на користь альтернативної, згідно якої пропорції Р1, і Р2 розрізняються з довірчою імовірністю  . Традиційно приймають, що якщо
. Традиційно приймають, що якщо  , то це достатньо, щоб відхилити нульову гіпотезу на заданому рівні значущості
, то це достатньо, щоб відхилити нульову гіпотезу на заданому рівні значущості  Якщо в результаті використання z-критерію було всановлено, що пропорції Р1 і Р2 розрізніяються, то для їх різниці корисно побудувати довірчий інтервал. Довірчий інтервал – це інтервал, відносно, якого із заданою імовірністю
Якщо в результаті використання z-критерію було всановлено, що пропорції Р1 і Р2 розрізніяються, то для їх різниці корисно побудувати довірчий інтервал. Довірчий інтервал – це інтервал, відносно, якого із заданою імовірністю  можна стверджувати, що він містить невідоме значення параметра:
можна стверджувати, що він містить невідоме значення параметра: 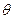 :
:  , де
, де 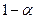 - довірча імовірність;
- довірча імовірність;  -процентний довірчий інтервал різниці середніх не містить нуля, то відмінності статистично значимі
-процентний довірчий інтервал різниці середніх не містить нуля, то відмінності статистично значимі  і, навпаки, якщо цей інтервал містить нуль, то відмінності статистично незначущі
і, навпаки, якщо цей інтервал містить нуль, то відмінності статистично незначущі  . Слід враховувати, що ширина довірчого інтервалу також характеризує ступінь нашого незнання: дуже широкий довірчий інтервал може служити лише вказівкою на те, що слід зібрати більше даних. Довірчі інтервали дають більше інформації про параметр, чим проста точкова оцінка, оскільки відмежовують відразу цілу сукупність допустимих значень. Для побудові довірчого інтервалу спочатку необхідно обчислити оцінку стандартної похибки різниці (
. Слід враховувати, що ширина довірчого інтервалу також характеризує ступінь нашого незнання: дуже широкий довірчий інтервал може служити лише вказівкою на те, що слід зібрати більше даних. Довірчі інтервали дають більше інформації про параметр, чим проста точкова оцінка, оскільки відмежовують відразу цілу сукупність допустимих значень. Для побудові довірчого інтервалу спочатку необхідно обчислити оцінку стандартної похибки різниці ( ) використовуючи наступну формулу:
) використовуючи наступну формулу: (2), де
(2), де  і
і 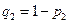 . У випадку коли
. У випадку коли  і
і  достатньо великі то
достатньо великі то  (3)
(3) - процентна точка стандартного нормального розподілу.
- процентна точка стандартного нормального розподілу.
 , що також дозволяє відкинути нульову гіпотезу на користь альтернативної.
, що також дозволяє відкинути нульову гіпотезу на користь альтернативної. . Таким чином, можна стверджувати, що дійсна різниця пропорцій Р1 і Р2 приблизно в 95% випадків потраплятиме в даний довірчий інтервал. Оскільки довірчий інтервал не включає значення 0 при заданому рівні імовірності, то це також підтверджує зроблені в п.1 виводи.
. Таким чином, можна стверджувати, що дійсна різниця пропорцій Р1 і Р2 приблизно в 95% випадків потраплятиме в даний довірчий інтервал. Оскільки довірчий інтервал не включає значення 0 при заданому рівні імовірності, то це також підтверджує зроблені в п.1 виводи.


