
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виявлення взаємозв'язків між вибірками. Кореляційний та регресійний аналізСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мета роботи: Навчитися знаходити взаємозв’язки між вибірками, здійснювати кореляційний і регересійний аналізи за результатами медико- біологічних досліджень. Забезпечення: персональний комп’ютер IBM PC AT, операційна оболонка Windows XP, текстовий процесор Word, електронні таблиці Microsoft Excel.
Теоретична частина Завдання №1. Виявлення взаємозв'язків між вибірками Кінцева мета будь-якого дослідження або наукового аналізу полягає у виявлені зв’язків (залежності між змінними. Філософія науки вчить, що не існує іншого способу представлення знання, окрім як у термінах залежності між кількостями або якостями, вираженими певними змінними. Таким чином, розвиток науки полягає у виявленні нових зв'язків між змінними. Незалежно від типу змінних вони пов'язані (залежні) між собою, якщо спостережувані значення цих змінних розподілені належним чином. Наприклад, зріст людини пов'язаний з масою її тіла, тому що зазвичай маса тіла високих індивідів більша, ніж осіб низьких на зріст. IQ (коефіцієнт інтелекту) пов'язаний з кількістю помилок у тесті, оскільки люди з високим значенням IQ припускаються меншої кількості помилок. Усі явища в природі та суспільстві взаємопов'язані. Відомі два види зв'язку між явищами (ознаками): функціональний та кореляційний. Функціональний зв'язок означає сувору залежність явищ. Наприклад, зі збільшенням радіусу обов'язково збільшується довжина кола та площа круга. Цей зв'язок має місце в точних науках. Кореляційний зв'язок спостерігається між явищами у медичних та біологічних дослідженнях. Наприклад, залежність маси тіла дитини від зросту, залежність захворюваності на черевний тиф від ступеня охоплення населення щепленням проти цього захворювання. Проте захворюваність на черевний тиф залежить не тільки від обсягу щеплень, а й від санітарного впорядкування, водопостачання, санітарної культури населення тощо. Метод на виявлення достовірності відмінності початкових даних Доказову медицину можна розглядати як новий підхід або технологію збирання, аналізу, узагальнення та інтерпретації наукової інформації початкових даних. Одна з причин виникнення доказової медицини — це збільшення обсягу наукової інформації, зокрема в галузі клінічної фармакології. Щороку в практику впроваджуються все нові і нові препарати. Вони активно вивчаються.
Важливим завданням статистичного аналізу даних є виявлення взаємозв'язків між вибірками. Для оцінки ступеня взаємозв'язку служить коефіцієнт кореляції. Коефіцієнт кореляції (r) - параметр, що характеризує ступінь лінійного взаємозв'язку між двома вибірками. Він знаходиться за допомогою співвідношення:
де ( Коефіцієнт кореляції змінюється від -1 (строга зворотна лінійна залежність) до 1 (строга пряма пропорційна залежність). При значенні 0 - лінійної залежності між двома вибірками немає. На практиці коефіцієнт кореляції приймає деякі проміжкові значення. Для оцінки ступеня взаємозв'язку можна керуватися наступними емпіричними правилами. Якщо коефіцієнт кореляції (r) по абсолютній величині (без врахування знаку) більший ніж 0,95, то прийнято вважати, що між параметрами існує практично лінійна залежність (пряма при додатному і зворотня при негативному r). Якщо коефіцієнт кореляції лежить в діапазоні від 0,8 до 0,95, говорять про сильний ступінь лінійного зв'язку між параметрами; 0,6 < r < 0,8 - говорять про наявність лінійного зв'язку між параметрами. При r < 0,4 вважають, що лінійний взаємозв'язок між параметрами виявити не вдалося.
1.1. Для виявлення ступені взаємозвязку необхідно ввести дані таблиці 6.1 в електронну таблицю. Прізвища пацієнтів ввести в стовпчик А. В комірки В1, С1, D1, E1, F1 відповідно ввести SAR, HR, Вага, Вік, ЧССНАВ. 1.2. В комірки В2:В11 вводимо значення SAR досліджуваної групи. Відповідно в комірки С1:C11, D1:D11, E1:E11, F1:F11 вводимо інші показники. Потім обчислюємо значення коефіцієнтів кореляції між вибірками. Для цього табличний курсор встановлюємо у вільну комірку. На панелі інструментів необхідно натиснути кнопку Вставка функций ( 1.3. Обчислити коефіцієнти кореляції між: - віком та іншими показниками; - вагою та іншими показниками; - систолічним артеріальним тиском і іншими показниками; - частотою серцевих скорочень та іншими показниками; - частотою серцевих скорочень після дозованого навантаження та іншими показниками. 1.4. Побудувати кореляційну матрицю і зробити відповідні висновки про кореляцію показників. Кореляційна матриця – це квадратна (або прямокутна) таблиця, в якій на перетині відповідних рядків та стовпчиків знаходиться коефіцієнт кореляції між відповідними параметрами. Комірки таблиці (див. табл. 9), в яких співпадають координати рядків і стовпчиків, містять значення 1, так як кожний параметр повністю корелює сам із собою.
Таблиця 6.1. Результати досліджень хворих
Примітка: SAR - систолічний артеріальний тиск; HR- частота серцевих скорочень; ЧССНАВ-частота серцевих скорочень після дозованого навантаження.
Таблиця 6.2. Приклад кореляційної матриці
Завдання №2 Дослідження впливу певних чинників на вимірювану величину Визначити вплив фактору віку та ваги на фізіологічні показники хворих приведених, в таблиці 6.1. При дослідженні дії на вимірювану величину (відгук) одного або декількох чинників використовується дисперсійний аналіз. Причому в однофакторному, двохфакторному і т.д. аналізі чинники, що впливають на результат, вважаються відомими, і мова йде тільки про з'ясування істотності або оцінку цього впливу. Для проведення дисперсійного аналізу необхідно: 1. Ввести дані в таблицю, так щоб в кожному стовпці опинилися дані, відповідні одному значенню досліджуваного чинника, а стовпці розташовувалися в порядку зростання величини досліджуваного чинника; 2. Виконати команду Сервис→Анализ данных→Инструменты анализа→Однофакторный дисперсионный анализ. 3. У діалоговому вікні, що з'явилося, задати Входной интервал, тобто ввести посилання на діапазон аналізуємих даних, що містить всі стовпці даних. Для цього слід виділити аналізовані дані. 4. В розділі Группировка перемикач встановлюється в положення По стовпцях; 5. Вказати вихідний діапазон, тобто ввести посилання на комірки, в які будуть виведені результати аналізу, або виділити їх.
Результати анализу. Вихідний діапазон включатиме результати дисперсійного аналізу: середні значення, дисперсії, критерій Фішера і інші показники. Інтерпретація результатів. Вплив досліджуваного чинника визначається по величині значущості критерію Фішера, яка знаходиться в таблиці Дисперсионный анализ на перетині рядка Между группами і стовпчика р -Значение. У випадку коли р-значение <0,05, критерій Фішера значущий і вплив досліджуваного чинника можна визнати доведеним. Демонстраційний приклад. Необхідно визначити, чи впливає вік на частоту серцевих скорочень (HR) за результатами досліджень, приведених в таблиці 8. Виконуємо команду Сервис→Анализ данны → Инструменты анализа→Однофакторный дисперсионный анализ. Натискаємо кнопку ОК. У діалоговому вікні, що з'явилося Однофакторный дисперсионный анализ задаємо Входной интервал А1:В11. В розділі Группировка перемикач встановлюється в положення по столбцам. Далі необхідно вказати вихідний діапазон, виділивши у таблиці вихідні дані. Результати аналізу. В результаті буде отримана таблиця з результатами дисперсійного аналізу. За даними результатами зробимо висновки про вплив досліджуваного чинника.
Завдання №3. Регресійний аналіз експериментальних даних Лінійний регресійний аналіз полягає в підборі графіка і його рівняння для набору спостережень. Регресія використовується для аналізу дії на окрему залежну змінну значень однієї або декількох незалежних змінних. В Пакете анализа експериментальні дані апроксимуються лінійним рівнянням:
де 1. Виконати команду Сервис→Анализ данных→Инструменты анализа→Регрессия.; 3. У діалоговому вікні, що з'явилося, задати Входной интервалY, тобто ввести посилання на діапазон аналізованих залежних даних, що містять один стовпець даних (виділити цей стовпець). 4. Вказати Входной интервал X, тобто ввести посилання на діапазон незалежних даних (виділити мішкою вхідні дані). 5. Вказати вихідний діапазон, тобто ввести посилання на комірки, в які будуть виведені результати аналізу. Для цього слід поставити перемикач в положення Выходной диапазон і віділити мишкою вихідні дані. 6. Натискається кнопка ОК. Результати аналізу. Вихідний діапазон включатиме результати дисперсійного аналізу, коефіцієнти регресії, стандартну похибку обчислення Інтерпретація результатів. Значення коефіцієнтів регресії знаходяться в стовпці Коэффициенты і відповідають:
Переменная Х1- Переменная Х2 -
Таблиця 6.3. Результати досліджень залежності товщини рубця від часу кріодеструкції
В стовпчику р-Значение приводиться достовірність відмінності відповідних коефіцієнтів від нуля. У випадках, коли р > 0,05, коефіцієнт може вважатися нульовим; це означає, що відповідна незалежна змінна практично не впливає на залежну змінну. Приведене значення R-квадрат, характеризує з яким ступенем точності отримане регресійне рівняння, що апроксимує початкові дані. Якщо R -квадрат > 0,95, говорять про високу точність апроксимації (модель добре описує явище). Якщо R -квадрат лежить в діапазоні від 0,8 до 0,95, то говорять про задовільну апроксимацію (модель в цілому адекватна описуваному явищу). Якщо R -квадрат < 0,6, прийнято вважати, що точність апроксимації недостатня і модель вимагає покращення (введення нових незалежних змінних, врахування нелінійностей і т. д.).
Практичне завдання №3. На підставірезультатів досліджень ефективної кріодеструкції шкіряних рубців різної товщини, приведених в таблиці 10, визначити передбачуваний час кріодеструкції з використанням табличного процесора Excel та графічного редактора Origin. Демонстраційний приклад Вводимо дані в табличний редактор Excel: товщина рубця — в діапазон А2:А9; час кріодеструкції - в діапазон В2:В9. Вибираємо пункт меню Сервис→Анализ данных → Регрессия. У діалоговому вікні, що появилося, задаємо Входной интервал Y (виділяємо дані В2-В9). Аналогічно указуємо Входной интерва л X, тобто ввести посилання на діапазон незалежних даних А8:А9. Далі указуємо вихідний діапазон (С2). 8.2. На основі отриманих результатів регресійного аналізу визначити аналітичну залежність часу кріодеструкції від товщини рубця. 8.3. За допомогою графічного редактора Origin візуалізувати отримані результати досліджень та встановити аналогічну аналітичну залежність товщини рубця від часу кріодеструкції. Для цього по наведеним табличним даним необхідно побудувати графік та відкрити меню Analysis і вибрати команду Fit Linear. Результати обчислення появляться у вікні програми. Практична робота №8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 ,
, ), (
), ( ),
),  ,(
,( ) – випадкові величини, що спостерігаються сумісно,
) – випадкові величини, що спостерігаються сумісно,  -середнє значення по вибірці
-середнє значення по вибірці  ,
,  -вибіркова дисперсія по виборці
-вибіркова дисперсія по виборці  -середнє значення по вибірці
-середнє значення по вибірці  ,
,  -вибіркова дисперсія по виборці
-вибіркова дисперсія по виборці  ). В вікні Мастер функций, що з’явилося вибрати категорію Статистические і функцію КОРРЕЛ, після чого натиснути кнопку ОК. Діапазон даних, між якими шукається кореляція ввести в поле Массив 1 і Массив 2, відповідно. У вільній комірці появиться величина коефіцієнта кореляції.
). В вікні Мастер функций, що з’явилося вибрати категорію Статистические і функцію КОРРЕЛ, після чого натиснути кнопку ОК. Діапазон даних, між якими шукається кореляція ввести в поле Массив 1 і Массив 2, відповідно. У вільній комірці появиться величина коефіцієнта кореляції.
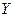 — залежна змінна, XI,..., XI6 — незалежні змінні
— залежна змінна, XI,..., XI6 — незалежні змінні  - шукані коефіцієнти регресії. Для отримання коефіцієнтів регресії необхідно:
- шукані коефіцієнти регресії. Для отримання коефіцієнтів регресії необхідно:
 ;
;


