
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Послідовність операцій при виборі критеріюСодержание книги
Поиск на нашем сайте Постановка задачі Порівняння показників контрольної та експериментальної вибірок. У нас є дві незалежні вибірки в яких ми порівнюємо середні значення деяких параметрів. Наприклад, дві групи хворих, лікування яких здійснювалося різними методами. Порівняння показників вибірки до і після експерименту. В даному випадку ми маємо справу з так званими зв'язними вибірками. Наприклад, значення певного показника в одній і тій же групі хворих до і після лікування. Чи можна вважати, що середнє значення показника дорівнює певному номінальному значенню? Для певного показника (наприклад, артеріальний тиск, частота пульсу) може існувати певне значення, котре вважається нормою (номінальне значення). Необхідно перевірити, чи можна вважати, що середнє значення показника в цій групі дорівнює нормі. Після перевірки цієї гіпотези для середнього, обов'язково потрібно побудувати довірчий інтервал і прослідкувати щоб для вибірки виконувалися необхідні умови. Порівняння розсіювання показників двох вибірок В деяких біологічних експериментах важливим є не середнє значення показника, а його розсіювання. Наприклад, необхідно вибрати препарат (метод лікування), для якого розсіювання контрольованої ознаки після застосування буде мінімальним. Чи можна вважати, що в декількох вибірках має місце одне і теж значення показника? Задача аналогічна попередній, але порівнюються не два типи впливу, а три і більше. Наприклад, ми застосовуємо для лікування різних груп хворих декілька препаратів. Чи можемо ми сказати, що результати лікування статистично не відрізняються?
Визначення додаткових умов вибору критерію Найпоширенішими додатковими умовами для вибору критерію є наступні умови: - рівні чи не рівні розміри вибірок? - рівні чи не рівні дисперсії вибірок, що порівнюються? - чи однакові закони розподілу вибірок, що порівнюються? Вимоги до вибірок При проведенні досліджень (особливо клінічних) необхідно забезпечити наступні вимоги до вибірки: Однорідність. При виборі впливу сукупності факторів, що вивчаються, ознаки, котрі нас цікавлять, не повинні суперечити одна одній. Наприклад, при дослідженні впливу кави на організм людини, в виборці досліджуваних не повинно бути людей, яких кава збуджує, і тих, яких від неї хилить на сон. В ряді випадків причини неоднорідності можуть бути невідомі і тому перед аналізом даних бажана перевірка вибірки методами кластерного аналізу. При виборі не повинно бути факторів, котрі сильно впливають на параметр, окрім тих, які ми вивчаємо. Якщо ми припускаємо, що фази Місяця впливають на ефективність дії препарату, то фазу Місяця необхідно враховувати як фактор або збирати вибірки, в яких фаза Місяця однакова.
Репрезентативність. (структурна відповідність). Вибірка, що вивчається, має бути репрезентативна генеральній сукупності. Це означає, що коли ми формуємо вибірку з сукупності, вона повинна відповідати наступним вимогам: - вид статистичного розподілу вибірки повинен відповідати розподілу генеральної сукупності; - величина вибірки повинна бути достатньою для відображення структури генеральної сукупності. У зв'язку з цим вибірка із хворих, які проходили курс лікування в одній клініці або покупці однієї аптеки не є репрезентативними за своєю структурою. Опитування, проведене по телефону, відображає думку лише власника телефону, а не всього населення, структура захворювання в різних областях різна. Висновки маркетингового дослідження не розповсюджується на невеликі міста. У тому випадку коли порівнюємо певні параметри двох вибірок, необхідно забезпечити рівність розподілу частот факторів, котрі мають вплив (стать, вік, серйозність захворювання і т.д.) у порівнюваних вибірках. Співпадання умов спостережень. Умови спостереження для окремих елементів вибірки або двох вибірок, що порівнюються, повинні співпадати. Найкращий спосіб це забезпечити - подвійний сліпий метод, при якому ні пацієнт, ні середній медичний персонал не знає, які ліки видаються конкретному хворому. Це дозволяє позбутися від ефекту навіювання (вплив якого можливий на 30-50% пацієнтів) і ефекту упередженості.
Використання табличного процесора Ехсеl для елементарної статистичної обробки даних
У пакеті Ехсеl крім Мастера функций є набір інструментів для аналізу даних, що називається Пакет анализа, який може бути використаний для вирішення завдань обробки медичних даних. Для цього необхідно: -встановити розділ Анализ даних в пакеті Ехсеl: -в меню Сервис вибрати команду Надстройки; -в списку, що з'явився, встановити прапорець Пакет анализа. Введення даних. Для використання пакету аналізу досліджувані дані слід представити у вигляді таблиці, де стовпцями є відповідні показники. При створенні таблиці Ехсе1 інформація вводиться в окремі комірки. Сукупність комірок, що містять аналізовані дані, називається вхідним діапазоном. Загальна послідовність обробки даних. Для використання статистичного пакету аналізу даних необхідно вибрати пункт меню Сервис→Анализ данных→Инструменты анализа. Ввести вхідний і вихідний діапазони і вибрати необхідні параметри. Якщо команда Анализ данных відсутня в меню Сервис, то необхідно встановити в Ехсеl пакет аналізу даних.
Практичні завдання Завдання №1. Знаходження достовірності різниць між змінними Наступним етапом після визначення основних статистичних характеристик є виявлення достовірності різниць між групами або змінними (перевірка статистичної гіпотези про рівність генеральних середніх). Розглянемо дві групи хворих тахікардією, одна із яких (контрольна) отримувала традиційне лікування, інша (досліджувана) отримувала лікування по новій методиці. Нижче наведені частоти серцевих скорочень (ЧСС) для кожної групи (ударів в хвилину).
Потрібно провести статистичний аналіз цих даних. 1.1. Знайти середнє значення. 1.2. Знайти стандартне відхилення 1.3. За формулою (1) розрахувати значення 1.4. Порівняти дані ЧСС досліджуваної групи з контрольною за допомогою Демонстраційний приклад Для оцінки достовірності відмінностей по критерію Ст’юдента приймається нульова гіпотеза, що середні вибірок рівні між собою. Потім обчислюється значення ймовірності того, що події (ЧСС хворих в обох вибірках), що вивчаються, відбулися випадковим чином. Для цього табличний курсор встановлюється у вільну комірку. На панелі інструментів необхідно натиснути кнопку Вставка функції (fх). У діалоговому вікні, що з'явилося, за допомогою майстра функцій вибрати категорію Статистичні і функцію ТТЕСТ, після чого натиснути кнопку ОК. Ввести діапазон даних контрольної групи в поле Массив 1. У полі Масив 2 ввести діапазон даних досліджуваної групи. У полі Хвосты завжди вводиться з клавіатури цифра «2» а в полі Тип з клавіатури введемо цифру «3». Нажати кнопку ОК. В комірці появится значение шуканої ймовірності. Зробити висновок про достовірність різниці між двома вибірками.
При використанні У другому випадку, коли одна і та ж група об'єктів породжує числовий матеріал для перевірки гіпотез про середні, використовується так званий парний
1.5. Виміряна температура двох груп хворих:
Визначити достовірність різниці між групами у випадку: 1) групи складаються з різних хворих; 2) групи складаються з одних і тих же хворих, але перша - до прийому жарознижуючого, а друга - після. Завдання №2. Порівняння частоти прояву ефекту з використанням z‑критерію. 2.1. Користуючись прикладом, приведеним в статті до практичної роботи №2, порівняти частоту виникнення небажаних побічних реакцій при лікуванні різними препаратами за результатами досліджень, запропонованих викладачем. Демонстраційний приклад. Порівняємо частоту виникнення побічних ефектів в контрольній та експериментальній групі за результатами досліджень, приведених в таблиці 6.2 (див. статтю до практичної роботи №2). Для цього, в робочому листі Ехсеl сформуємо таблицю спряженості і введемо в неї початкові дані. Загальний вид робочого листа приведений на рис. 6.3.
Рис.6.3 Загальний вид робочого листа 2.2. Розрахуємо значення частоти виникнення побічних ефектів в двох групах. Результати розмістити в комірки Н5; Н6; Н7. 2.3. Розрахуємо значення z-критерію. Для цього в комірку G8 введемо відповідну формулу (див. текст статі практичної роботи №2). 2.4. Відповідним чином розрахувати вибіркову різницю, стандартну помилку різниці, ліву та праву границю довірчого інтервалу. 2.5. Задамо рівень значущості 2.6. Знайдемо критичне значення стандартного нормального розподілу для рівня 2.7. Розрахуємо досягнутий рівень значущості. Для цього в комірку G15 вставимо функцію (1 - НОРМСТРАСП(G8))*2. 2.8. Зробити висновок про ймовірність виникнення негативних побічних ефектів при лікуванні пацієнтів двох різних груп. Практичне завдання №2 2.9. За результатами досліджень, запропонованих викладачем, порівняти частоту виникнення небажаних побічних реакцій при лікуванні різними препаратами. Завдання №3 Порівняння відносних величини прояву досліджуваного ефекту в двох групах з використання критерію Демонстраційний приклад. Бувають ситуації коли необхідно порівняти дві відносні, чи виражені в процентах величини. Наприклад у випадку перевірки ефективності дії вакцини або двох методів лікування. Як приклад застосування критерію Нульовою гіпотезою (Н0), яку ми збираємося перевіряти, приймемо наступну: частота виникнення побічних реакцій не залежить від способу лікування і однакова для обох (контрольної і експериментальної) груп. З погляду математичної статистики це завдання перевірки незалежності двох ознак. Для використання згаданого критерію дані, отримані в результаті проведених досліджень, необхідно представити у вигляді чотирьохклітинної таблиці спряженості ознак. Для застосування даного критерію необхідно, щоб в кожній клітині даної таблиці очікувана частота була не нижча 0,05. Якщо дана умова не виконується, то необхідно застосовувати точний критерій Фішера для отримання досягнутого рівня значущості р, не використовуючи апроксимацію на основі розподілу
Іншими словами, якщо ми об'єднаємо обидві групи, то це буде частка пацієнтів, що мають ознаку, що цікавить нас, в об'єднаній групі. У разі справедливості нульової гіпотези частка таких пацієнтів в кожній групі повинна бути рівна частці в узагальненій вибірці (
Таблиця 6.3. Частота виникнення побічних реакцій у пацієнтів і їх доля у відповідних групах
Якщо ми об'єднаємо обидві вибірки (експериментальну і контрольну групи), то загальне число пацієнтів буде рівне 217, а кількість пацієнтів, у яких були виражені побічні реакції в обох підгрупах становить 40 (
Як видно, значення спостережуваних частот відрізняються від очікуваних. Проте необхідно з'ясувати, чи є ця відмінність статистично значущою і чи можемо ми розповсюдити отримані результати на всю вибірку. Для цього застосуємо критерій
Сумування проводиться по всіх клітках таблиці спряженості. Проте, враховуючи, що неперервний розподіл
Включення у формулу поправки на неперервність сприяє більшій відповідності між ймовірностями в порівнянні з випадком, коли вона не використовується, і її рекомендується застосовувати завжди. На практиці досить часто користуються іншим виразом критерію
де позначення, приведені в даній формулі, відповідають таким в табл. 7. Вирази (7) і (8) еквівалентні - за допомогою алгебраїчних перетворень з одного можна отримати інший. Розраховане значення Обробимо дані приведеного вище прикладу. Для цього на робочому листі Ехсеl сформуємо таблицю спряженості і введемо в неї початкові дані. Загальний вид робочого листа приведений на рис. 6.4. 3.1. Приймемо гіпотезу H0: пропорції частоти виникнення побічних явищ в двох порівнюваних групах однакові; H1: пропорції частоти виникнення побічних явищ в двох порівнюваних групах статистично значущо розрізняються. 3.2. Задамо рівень значущості
Рис.6.4 Загальний вид робочого листа
3.3. Розрахуємо очікувані частоти згідно виразу (1), внісши до комірок робочого листа відповідні формули (комірки С8;Е8;D5;D6; F5;F6;H5;H6;H7). 3.4. Розрахуємо критеріальне значення використовуючи вираз (7). Для цього в комірку Е9 введемо відповідну формулу. 3.5. Розрахуємо досягнутий рівень значущості, використовуючи вбудовану в Ехсеl функцію розрахунку ймовірності розподілу 3.6. Рішення щодо ухвалення або відхилення нульової гіпотези може залежати від досягнутого рівня значущості і критичного значення розподілу 3.7. На підставі отриманих результатів можна зробити наступний висновок: існує статистично значуща відмінність в пропорціях частоти виникнення побічних реакцій у хворих експериментальної і контрольної груп. У пацієнтів контрольної групи частота виникнення побічних реакцій вища (31,4%) ніж в експериментальній (14,5%).
Практичне завдання №3. 3.8.Порівняти відносні величини прояву побічного ефекту в двох досліджуваних групах з використання критерію
Практична робота №7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 450; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |

 -критерію Ст’юдента. Обчислене значення
-критерію Ст’юдента. Обчислене значення  порівняти із табличним (див. додаток №2) з врахуванням числа ступеней вільності. Зробити відповідний висновок про достовірність різниці між ЧСС контрольної та досліджуваної групи.
порівняти із табличним (див. додаток №2) з врахуванням числа ступеней вільності. Зробити відповідний висновок про достовірність різниці між ЧСС контрольної та досліджуваної групи.
 =0.05 (комірка G9).
=0.05 (комірка G9). . Для цього в комірку G10 вставимо функцію НОРМСТОБР(1-G9/2).
. Для цього в комірку G10 вставимо функцію НОРМСТОБР(1-G9/2).
 -квадрат розглянемо порівняння двох методів лікування (експериментального і контрольного) за допомогою зіставлення частоти виникнення небажаних побічних реакцій в експериментальній і контрольній групах.
-квадрат розглянемо порівняння двох методів лікування (експериментального і контрольного) за допомогою зіставлення частоти виникнення небажаних побічних реакцій в експериментальній і контрольній групах. (5)
(5) ). На основі цього можна розрахувати для кожної клітки чотирьохклітинної таблиці значення частот, які очікуватимуться, якщо нульова гіпотеза справедлива. Розглянемо це на основі даних, приведених в табл. 6.3.
). На основі цього можна розрахувати для кожної клітки чотирьохклітинної таблиці значення частот, які очікуватимуться, якщо нульова гіпотеза справедлива. Розглянемо це на основі даних, приведених в табл. 6.3.



 )
)

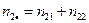





 ). Тоді в об'єднаній вибірці частка пацієнтів, у яких відмічені побічні явища, складатиме
). Тоді в об'єднаній вибірці частка пацієнтів, у яких відмічені побічні явища, складатиме  Відповідно, частка пацієнтів в об'єднаній вибірці, у яких побічні явища не виявлені, буде рівна 81,57%. Як вже наголошувалося раніше, за умови справедливості нульової гіпотези обчислені пропорції повинні дотримуватися (або бути досить близькими) в кожній групі окремо. Обчислимо ці значення частот:
Відповідно, частка пацієнтів в об'єднаній вибірці, у яких побічні явища не виявлені, буде рівна 81,57%. Як вже наголошувалося раніше, за умови справедливості нульової гіпотези обчислені пропорції повинні дотримуватися (або бути досить близькими) в кожній групі окремо. Обчислимо ці значення частот: 


 . Іноді очікувані частоти називають теоретичними. У наступній таблиці приведені спостережувані і очікувані частоти.
. Іноді очікувані частоти називають теоретичними. У наступній таблиці приведені спостережувані і очікувані частоти. , а очікувану - через
, а очікувану - через  , матиме наступний вигляд:
, матиме наступний вигляд: (6)
(6) (7)
(7) (8)
(8)
 воно буде рівне 3.84, що значно менше експериментального (6,34). Це також дає нам повне право на заданому рівні значущості відхилити нульову гіпотезу.
воно буде рівне 3.84, що значно менше експериментального (6,34). Це також дає нам повне право на заданому рівні значущості відхилити нульову гіпотезу.


