
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання медичних та біологічних об’єктів і явищСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мета роботи: ознайомлення з теоретичними основами фізичного, математичного та комп’ютерного моделювання біологічних і медичних явищ та процесів. Засвоєння навиків використання та роботи зі спеціалізованими пакетами прикладних програм для комп’ютерного моделювання фізіологічних реакцій організму. Короткі теоретичні відомості
Поняття моделювання. Застосування та вимоги до моделей.
1. Модель, як засіб пізнання дійсності. Наука являє собою відображення в уяві людини (модель) реальних процесів, що відбуваються у природі. Приклад - електромагнітне поле, ідеальний газ, вакуум, «чорні дірки» і т.д. 2. Модель, як засіб спілкування. Розповідаючи про певний об’єкт або описуючи якусь подію ми, тим самим, створюємо модель реального об’єкта або події. 3. Модель, як засіб навчання. Сюди можна віднести різного роду тренажери, що допомагають людям отримати навики керування складними механізмами і поводження в екстремальних ситуаціях. 4. Модель, як засіб прогнозування. Моделюючи якийсь реальний процес або явище ми можемо спрогнозувати їх поведінку через певний час або у конкретних умовах. 5. Модель, як спосіб постановки експериментів. Тут модель застосовується, коли постановка експерименту на реальному об’єкті сильно ускладнена або взагалі неможлива. Приклад – моделі погасання зірок і утворення наднових.
Вимоги до моделей: 1. Модель повинна бути адекватною, тобто відображати усі суттєві для розгляду властивості реального об’єкта. 2. Витрати на утворення моделі повинні бути меншими за витрати на утворення оригіналу. 3. Необхідно чітко визначити правила інтерпретації результатів.
Класифікація моделей
За засобами побудови розрізняють: а) словесні (або вербальні, текстові) моделі. Це моделі, утворені мовними засобами. Приклад – міліцейський протокол з місця події. б) натурні (або фізичні) моделі. Це моделі, що мають реальне матеріальне втілення; їх можна осягнути органами відчуттів людини. Приклад – макет сонячної системи. в) абстрактні (або знакові, математичні). Це моделі побудовані на основі математичних засобів. г) комп’ютерні моделі. Це моделі, побудовані комп’ютерними засобами на основі інформаційних технологій. За предметною областю розрізняють: а) біологічні моделі б) економічні моделі в) фізичні моделі г) хімічні моделі д) медичні моделі е) соціальні моделі і т.д. За метою моделювання розрізняють моделі: а) дескриптивні (описуючі). Такі моделі повинні описувати досліджуваний об’єкт, процес або явище. б) оптимізаційні. Ці моделі призначені для пошуку найкращого рішення серед багатьох можливих. Тут завжди є кілька вхідних параметрів, змінюючи які, можна визначити оптимальні параметри вихідних величин. в ) навчальні. Такі моделі призначені для оволодіння навиками керування складними механізмами (тренажери). г) ігрові. Призначені для ефективного відпочинку та цікавого проводження часу. д) імітаційні. Призначені для більш-менш точної імітації реальних процесів і явищ.
За поведінкою розрізняють моделі: а) детерміновані - вихідні параметри моделі є однозначними функціями вхідних). б) стохастичні (статистичні) - вихідні параметри визначаються з певною ймовірністю. в) статичні (стаціонарні, квазістаціонарні) – параметри моделі незмінні (слабо змінюються) у часі. г) динамічні (нестаціонарні) – параметри моделі є функціями часу. д) аналогові – параметри моделі є неперервними функціями. е) цифрові - параметри моделі є дискретними.
Види моделювання Розрізняють фізичне, математичне та комп’ютерне моделювання. Фізичне моделювання – це моделювання на об’єктах, що мають однакову фізичну природу з об’єктом-оригіналом. Приклад – зменшена копія реального літака, що досліджується у аеродинамічній трубі. Для фізичного моделювання необхідно забезпечити фізичну подібність моделі і об’єкта. Фізична подібність забезпечується лише при рівності всіх однотипних безрозмірних комплексів (критеріїв подібності) у вихідних точках моделі і об’єкта. Приклад. Критерій (число) Рейнольдса:
де V – швидкість течії, L - лінійний розмір, l - кінематична в’язкість середовища. Для забезпечення фізичної подібності реального літака з його зменшеною копією необхідно, щоб критерії подібності Re, обраховані окремо для літака і його моделі були одинакові. Це означає, що для зменшеної в 10 разів моделі літака швидкість течії у гідродинамічній трубі необхідно збільшити в 10 разів, або у 10 разів зменшити в’язкість середовища. Тільки тоді критерій Рейнольдса буде однаковим для літака і моделі, а значить, буде забезпечена фізична подібність цих об’єктів. Критеріїв подібності є дуже багато. Існують критерії гідродинамічної, теплової, хімічної і т.д. подібності. Зрозуміло, що забезпечити виконання всіх критеріїв дуже складно, а іноді, і неможливо. Однак для адекватності моделі і об’єкта необхідно забезпечити виконання найбільш суттєвих з них, що мають безпосереднє відношення до мети моделювання. Перевагою фізичного моделювання є наочність – фізична модель наглядно відображає будову та необхідні для розв’язку задачі властивості об’єкта. Недоліком такого типу моделювання є неуніверсальність – для кожного нового об’єкта необхідно створювати нову модель. Математичне моделювання – це моделювання об’єкта шляхом розв’язку рівнянь його математичної моделі. При такому типі моделювання важливу роль відіграє математична подібність. Для прикладу, запишемо рівняння трьох фізичних процесів: теплопровідності, дифузії та протікання струму (перенос заряду). Для теплопровідності потік тепла q пропорційний градієнту температури dT / dx з коефіцієнтом пропорційності l (коефіцієнтом теплопровідності):
Для процесу дифузії потік речовини w пропорційний градієнту концентрації dc / dx з коефіцієнтом пропорційності D (коефіцієнтом дифузії):
Для процесу проходження електричного струму потік заряду i пропорційний градієнту потенціала du / dx з коефіцієнтом пропорційності r (провідність):
Як видно, абсолютно різні фізичні процеси описуються ідентичними математичними рівняннями. Це одна з переваг математичного моделювання – універсальність. Адже модель теплопровідності можна з успіхом застосувати, наприклад, для опису процеса дифузії. Етапи математичного моделювання: 1) складання математичного опису; 2) розв’язок рівнянь математичного опису; 3) перевірка адекватності моделі; 4) вибір моделі (якщо їх декілька). Якщо набір всіх вхідних параметрів моделі X 1, X 2, ¼, X N позначити через
Комп’ютерне моделювання – це моделювання комп’ютерними засобами з використанням інформаційних технологій. Метою комп’ютерного моделювання є побудова інформаційної моделі об’єкта. Інформаційна модель – це набір величин, характеристик, властивостей, що адекватно описують об’єкт, процес або явище. Наприклад, інформаційна модель Сонячної системи має містити перелік небесних тіл (планет) з вказаними параметрами для кожної планети – маса, радіус, період обертання навколо Сонця, власний період обертання навколо своєї осі, і т.д. Етапи комп’ютерного моделювання:
Проаналізувавши об’єкт складаємо формальну модель, шо містить: 1) набір постійних величин (констант); 2) набір змінних величин; 3) формули і алгоритми, що зв’язують змінні у кожному стані об’єкта; 4) формули і алгоритми, що описують зміну станів об’єкта. Використовуючи формальну модель, складаємо алгоритм та програмуємо модель. Програмування може відбуватися як на універсальних мовах програмування високого рівня (Pascal, C, Basic, Delphi), так і на спеціалізованих, призначених для моделювання – Simula, GPSS та ін.). При програмуванні особливу увагу слід приділяти способам виводу результатів – табличному, графічному або анімаційному. Після програмування та тестування проводиться комп’ютерний експеримент, де за вхідними даними отримуємо набір вихідних і, таким чином, складаємо інформаційну модель об’єкта. Дуже часто, при комп’ютерному моделюванні математичної моделі об’єкта використовуються пакети прикладних програм (математичні процесори) – MatLab, Maple, MatCad, Matematica та ін. У цьому випадку відпадає необхідність в традиційному програмуванні на мовах високого рівня.
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.007 с.) |

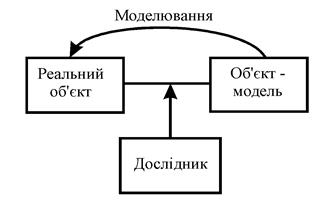 Модель – штучно створений об’єкт, що відображає будову та властивості реального об’єкта. Таким чином, дослідник завжди має справу з двома об’єктами – реальним об’єктом (процесом, явищем) та його моделлю (див.рис.1). Моделі виникли дуже давно – наскальні рисунки, мова, наука – все це є прикладом моделей. Моделювання – процес заміщення реального об’єкта його моделлю з метою вивчення будови реального об’єкта або передачі інформації про його властивості. Існують п’ять випадків застосування моделей:
Модель – штучно створений об’єкт, що відображає будову та властивості реального об’єкта. Таким чином, дослідник завжди має справу з двома об’єктами – реальним об’єктом (процесом, явищем) та його моделлю (див.рис.1). Моделі виникли дуже давно – наскальні рисунки, мова, наука – все це є прикладом моделей. Моделювання – процес заміщення реального об’єкта його моделлю з метою вивчення будови реального об’єкта або передачі інформації про його властивості. Існують п’ять випадків застосування моделей: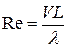 , (1)
, (1)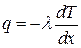 . (2)
. (2) . (3)
. (3) . (4)
. (4) , а набір вихідних параметрів Y 1, Y 2, ¼, Y M через
, а набір вихідних параметрів Y 1, Y 2, ¼, Y M через  , то під математичною моделлю об’єкта (рис.2) розуміють функцію
, то під математичною моделлю об’єкта (рис.2) розуміють функцію . (5)
. (5)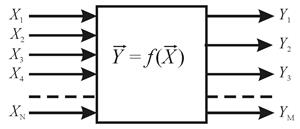 Окрім універсальності, перевагами математичного моделювання є дешевизна, можливість вільного керування параметрами та можливість розкладу процесу на складові (декомпозиція).
Окрім універсальності, перевагами математичного моделювання є дешевизна, можливість вільного керування параметрами та можливість розкладу процесу на складові (декомпозиція).



