
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи стохастичного факторного аналізуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функціонування економіки України в ринковому середовищі потребує вивчення і врахування дії цілого комплексу взаємопов'язаних факторів для оперативного прийняття та реалізації зважених управлінських рішень. При цьому традиційних методів та методів детермінованого факторного аналізу вже недостатньо у зв'язку з обмеженістю їх аналітичних можливостей, недостатністю інформаційного забезпечення тощо. Тому виникає необхідність ширшого застосування методів стохастичного факторного аналізу, які, на відміну від жорстко регламентованих методів детермінованого аналізу, основаних на функціональній залежності результативного показника від факторних, дають змогу врахувати вплив сукупності факторів, що носять імовірнісний, невизначений характер. До методів стохастичного факторного аналізу належать: дисперсійний, регресійний, кореляційний, компонентний, багатовимірний та інші види аналізу. Дисперсійний аналіз Дисперсія (лат. dispersio – розсіювання) часто застосовується в теорії ймовірностей і математичній статистиці. Означає ступінь розсіювання навколо середнього значення випадкової величини. У статистичному розумінні дисперсія є середнє арифметичне із квадратів відхилень величин від їх середнього арифметичного. На практиці при проведенні аналізу економічного стану підприємства чи галузі часто необхідно оцінити розсіювання можливих значень випадкової величини навколо її середнього значення, а також виявити та виміряти силу зв'язку між факторними та результативною ознаками. Дисперсійний аналіз – це статистичний метод, призначений для встановлення структури зв'язку між результативною та факторними ознаками. Він дає змогу визначити вплив одного або декількох факторів на результативний показник. Дисперсійний аналіз може застосовуватися за обмеженої кількості одиниць спостереження. До того ж він особливо ефективний в умовах, коли результативна ознака суттєво змінюється під одночасною дією кількох факторів з неоднаковою силою впливу. Дисперсійний метод аналізу відіграє велику роль в економічних дослідженнях завдяки тому, що він має самостійне значення. Завдяки цьому методу вирішуються такі завдання: – кількісне вимірювання сили впливу факторних ознак та їх сполучень на результативну;
– оцінка вірогідності впливу та його довірчих меж; – аналіз окремих середніх і статистична оцінка їх різниці. Крім того, у поглибленому аналізі дисперсійний метод може виконувати допоміжні функції, які дають змогу обґрунтовано використовувати інші методи аналізу. Розв'язання задачі виміру зв'язку спирається на розкладення суми квадратів відхилень досліджуваних значень результативної ознаки від загальної середньої на окремі частини, які обумовлюють зміну цієї ознаки. Якщо сукупність розбита на групи, то при цьому розраховуються загальна, групова, середня з групових і міжгрупова дисперсії. Загальна дисперсія ( де f – обсяг сукупності (кількість одиниць). Загальна дисперсія відображає варіацію досліджуваної ознаки за рахунок усіх умов, які впливають на неї у цій сукупності. Групова дисперсія ( де і – порядковий номер х та f в межах групи. Групова дисперсія характеризує варіацію ознаки в межах групи за рахунок всіх інших факторів за виключенням того, який покладений в основу групування. Щоб виміряти таку варіацію для сукупності в цілому, необхідно знайти середню із групових дисперсій. Середня з групових дисперсій ( Середня з групових дисперсій характеризує випадкову варіацію в кожній окремій групі. Ця варіація виникає під впливом інших факторів, що не враховуються, і не залежить від ознаки-фактора, покладеної в основу групування. Міжгрупова дисперсія ( Приклад. За даними табл. 12.1 зробити дисперсійний аналіз варіації урожайності озимої пшениці за двома виробничими підрозділами. При цьому другий підрозділ вніс мінеральні добрива, а перший – ні. Таблиця 12.1. Посівні площі та урожайність озимої пшениці в господарстві за двома виробничими підрозділами
Розрахуємо спочатку середню врожайність по господарству: Далі визначаємо:
Визначимо середню з групових дисперсій як середню арифметичну зважену із групових дисперсій: Знайдемо міжгрупову дисперсію: Тоді загальна дисперсія за урожайністю озимих зернових становитиме: Отже, про зв'язок між досліджуваними ознаками можна судити за допомогою коефіцієнта детермінації, який є відношенням міжгрупової дисперсії до загальної і записується у вигляді формули Коефіцієнт детермінації показує ступінь участі факторної ознаки у формуванні загальної змінюваності результативної ознаки. Зокрема, щодо нашого прикладу ступінь впливу кількості внесених добрив на урожайність зернових становить 80,5%: Ступінь впливу інших неврахованих факторів на результативну ознаку обчислюють за співвідношенням Рівень впливу інших неврахованих чинників дорівнює 19,5%. Проте найчастіше в економічному аналізі в ролі показника тісноти зв'язку застосовується кореляційне відношення (емпіричне), яке є коренем другого ступеня із коефіцієнта детермінації. Формула його така: У нашому прикладі Це свідчить про те, що мінеральні добрива суттєво впливають на урожайність озимої пшениці. Для підтвердження істотності зв'язку використаємо критерій Фішера де n – число одиниць сукупності; m – кількість груп. Отже, За допомогою таблиці критичних значень F-критерію порівняємо отриманий критерій із критичним значенням для рівня ймовірності 0,95. Для рівня значимості а = 0,05 табличне значення не перевищує 2,99. Оскільки розраховане значення критерію Фішера більше критичного (922,7 > 2,99), то це підтверджує істотність зв'язку між кількістю внесених добрив і урожайністю озимої пшениці. Регресійний аналіз Під терміном " регресія " розуміють рух назад, повернення до попереднього стану. Названий термін ввів у кінці XIX ст. Френсіс Галтон. В результаті проведеного ним дослідження зв'язку між зростом батьків і дітей, виявилося, що наявна обернена залежність. Так, у батьків з дуже високим зростом діти мають менший зріст порівняно з середнім зростом батьків. І, навпаки, у дуже низьких батьків середній зріст дітей вищий. В одному і другому випадку середній зріст дітей прямує (повертається) до середнього зросту населення певної місцевості. Саме такою залежністю і пояснюють вибір терміна "регресія". Регресійний аналіз (англ. regression analysis) – це метод визначення відокремленого і спільного впливу факторів на результативну ознаку та кількісної оцінки цього впливу шляхом використання відповідних критеріїв. Регресійний аналіз проводиться на основі побудованого рівняння регресії і визначає внесок кожної незалежної змінної у варіацію досліджуваної (прогнозованої) залежної змінної величини.
Основним завданням регресійного аналізу є визначення впливу факторів на результативний показник (в абсолютних показниках). Передусім для цього необхідно підібрати та обґрунтувати рівняння зв'язку, що відповідає характеру аналітичної стохастичної залежності між досліджуваними ознаками. Рівняння регресії показує як в середньому змінюється результативна ознака ( У загальному вигляді рівняння регресії можна представити так: де х – незалежні змінні величини (фактори). Залежно від кількості змінних величин виділяють різні види регресійного аналізу. Якщо змінна величина завжди одна, то змінних може бути як одна, так і декілька. Виходячи з цього, виділяють два види регресійного аналізу: парний (простий) регресійний аналіз і регресійний аналіз на основі множинної регресії, або багатофакторний. Парний регресійний аналіз – вид регресійного аналізу, що включає у себе розгляд однієї незалежної змінної величини, а багатофакторний – відповідно дві величини і більше. Зважаючи на характер зв'язку, в регресійному аналізі можуть використовуватися лінійні та нелінійні функції. Для визначення характеру залежності та, відповідно, побудови рівняння регресії доцільно застосувати графічний метод, порівняння рівнобіжних рядів вихідних даних, табличний метод. Так, графічний метод дає найбільш наочну картину розміщення крапок на графіку, завдяки чому можна виявити напрям і вид залежності між досліджуваними показниками: прямолінійна чи криволінійна. За допомогою порівняння рівнобіжних рядів ознак можна спостерігати за рівномірністю їх взаємних змін. Якщо зміна факторної ознаки (х) призводить до відносно рівномірної зміни результативної ( Найпростішим рівнянням парної регресії, що описує лінійну залежність між факторною і результативною ознаками, є рівняння прямої, яке має такий вигляд: де х – незалежна змінна (факторна ознака), яка використовується для визначення залежної змінної. Параметри рівняння обчислюються на основі системи нормальних рівнянь методом найменших квадратів:
Звідси Для зручності розрахунків регресійного та кореляційного аналізу (розглянемо далі) доцільно використати таку форму таблиці (табл. 12.2). Таблиця 12.2. Вихідні та розрахункові дані для обчислення регресійно-кореляційних характеристик (парна прямолінійна кореляція)
Основне змістовне навантаження в рівнянні регресії несе коефіцієнт регресії. Найчастіше застосовуються лінійні рівняння або приведені до лінійного вигляду. Коефіцієнт регресії – це кутовий коефіцієнт у прямолінійному рівнянні кореляційного зв'язку. У лінійній функції рівняння регресії він показує на скільки одиниць в середньому зміниться результативна ознака (у) при зміні факторної ознаки (х) на одиницю свого натурального виміру. Тобто, коефіцієнт регресії – це варіація у, яка припадає на одиницю варіації х. Коефіцієнт регресії має одиницю виміру результативної ознаки. За наявності прямого зв'язку коефіцієнт регресії є додатною величиною, а за зворотного зв'язку – від'ємною. Параметр а0 – вільний член рівняння регресії, тобто це значення у при х=0. Цей показник має тільки розрахункове значення у випадках, коли х не має нульових значень. У разі, коли зі зміною факторної ознаки результативна змінюється нерівномірно, використовуються нелінійні функції. Так, якщо зміна факторного показника сприяла прискореній динаміці результативного показника (наприклад, вплив обсягу грошової маси на рівень інфляції), доцільно використати степеневу функцію: У випадку, коли під впливом факторної ознаки результативна змінюється нерівномірно, причому з уповільненням, використовується рівняння гіперболи: Прикладом такої залежності є залежність рівня продуктивності праці робітників від рівня їх заробітної плати. Якщо зміна факторної ознаки супроводжується нерівномірною варіацією факторної ознаки із зміною напряму зв'язку, нелінійна регресія описується рівнянням параболи: Так, за допомогою функції параболи можна виразити залежність урожайності культур від кількості опадів. Приклад. За даними 25 заводів дослідити залежність між рівнями озброєності праці основними засобами та її продуктивністю, використовуючи регресійний аналіз (табл. 12.3). Таблиця 12.3. Озброєність праці основними засобами та рівень її продуктивності в групі заводів України, тис. грн
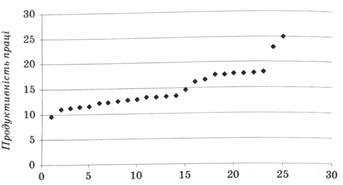
Паралельне зіставлення рядів значень рівнів озброєності праці основними засобами та її продуктивності, а також крапковий графік "кореляційного поля" (рис. 12.1) свідчать про наявність і напрям зв'язку (прямий) між наведеними показниками. Причому зміна озброєності праці (факторної ознаки х) приводить до відносно рівномірної зміни продуктивності праці (результативної ознаки у), що видно із графіка.
Рис. 12.1. Крапковий графік рівнів озброєності праці основними засобами та її продуктивності по 25 заводах України, тис. грн Отже, можна зробити висновок про наявність між зазначеними ознаками парного прямолінійного зв'язку, який виражається найпростішим рівнянням регресії лінійної функції де Для зручності розрахунків скористаємося наведеними нижче формулами, в які підставляємо попередньо обчислені необхідні розрахункові дані (табл. 12.1): Рівняння залежності матиме такий вигляд: Перевірка: Зобразимо графічно залежність між рівнями озброєності праці основними засобами та її продуктивністю, використавши рівняння регресії (рис. 12.2).
Рис. 12.2. Залежність між рівнями озброєності та продуктивності праці Якщо підставити в отримане рівняння регресії відповідні значення фактора (х) по заводах, то одержимо вирівняні значення продуктивності праці залежно від озброєності її основними засобами. Результати розрахунків наведені в табл. 12.3 (остання графа). З рівняння регресії видно, що підвищення озброєності праці основними засобами на одну тисячу гривень забезпечує підвищення рівня продуктивності праці на 0,95 тис. грн. Якщо б на заводі під № 1 озброєність праці була вище середньої, наприклад 17,9 тис. грн, то виробіток продукції на одного працівника становив би 19,8 тис. грн: Величина 17,9, яка взята на заводі, де озброєність праці перевищує середнє її значення – 14,8 тис. грн, називається середньою прогресивною. Таким чином, регресійний аналіз може бути використаний ще й для визначення резервів шляхом застосування середньопрогресивного значення факторіальної ознаки. У наведеному прикладі цей резерв мають 19 заводів, що мають виробіток продукції на одного працівника менший за 19,8 тис. грн. Також слід зазначити, що регресійний аналіз доцільно застосовувати для обґрунтування проектних, прогнозних чи очікуваних показників. Для цього необхідно підставити в одержане рівняння регресії проектне значення фактора. Зокрема, якщо б заводу № 7 поставити за мету доведення рівня озброєності праці основними засобами до 20 тис. грн, то можна зробити прогноз продуктивності праці, яка становитиме 21,8 тис. грн: Безумовно, що при застосуванні регресійного аналізу дотримуються деяких умовностей. Так, попередньо обумовлюється, що дія інших факторів, крім взятого за факторну ознаку, залишиться незмінною, а в дослідженні взято тільки один фактор. Проте останню умовність можна усунути за допомогою застосування множинної регресії та кореляції, за яких підбирається значна кількість факторів. Аналіз на основі множинної регресії (анг. multiple regression analysis) – вид регресійного аналізу, який ґрунтується на використанні в рівнянні регресії більше, ніж однієї незалежної змінної. Так, його застосовують при прогнозуванні попиту. Причому спочатку ідентифікуються фактори, що визначають попит, потім встановлюються наявні між ними взаємозв'язки та прогнозуються ймовірні майбутні їх значення. На основі отриманих даних виводиться прогнозне значення попиту. Багатофакторне рівняння множинної регресії при лінійній залежності має такий вигляд: де n – кількість незалежних змінних. Визначення параметрів множинної регресії вимагає трудомістких розрахунків із застосуванням комп'ютерних інформаційних систем. Однак одержані результати будуть достовірними і можуть широко використовуватися в економічній та управлінській діяльності насамперед для складання довгострокових прогнозів. Відомо, що однофакторна модель придатна для короткострокових прогнозів (на 2–3 роки). Метод регресійного аналізу вважається найдосконалішим з усіх використовуваних нині нормативно-параметричних методів. Він широко застосовується для аналізу та встановлення рівня і співвідношень вартості продукції, яка характеризується наявністю одного або декількох техніко-економічних параметрів, що характеризують головні споживчі якості. Регресивний аналіз надає можливість знайти емпіричну форму залежності ціни від техніко-економічних параметрів товарів і виробів. При цьому він виступає в ролі цільової функції параметрів. Метод регресійного аналізу особливо ефективний за умови здійснення розрахунків за допомогою сучасних інформаційних технологій і систем.
Кореляційний аналіз Кореляція дослівно з латинської "correlation" – відношення, тобто це означає співвідношення, відповідність речей, понять. Кореляційним зв'язком називається такий зв'язок між ознаками суспільно-економічних явищ, за якого на величину результативної ознаки крім факторної впливають багато інших ознак, які можуть діяти в різних напрямах одночасно чи послідовно. Цей зв'язок характеризується тим, що між факторною і результативною ознаками немає повної відповідності, а лише є певне співвідношення. Особливістю кореляційного зв'язку є те, що кожному значенню факторної ознаки відповідає не одне, а ціла низка значень результативної ознаки. Кореляційний зв'язок можна виявити тільки у вигляді загальної тенденції при масовому порівнянні факторів. Кореляційний аналіз (кореляційний метод) – метод дослідження взаємозалежності ознак у генеральній сукупності, які є випадковими величинами з нормальним характером розподілу. Основними вимогами до застосування кореляційного аналізу є достатня кількість спостережень, сукупності факторних і результативних показників, а також їх кількісний вимір і відображення в інформаційних джерелах. Застосування кореляційного аналізу тісно пов'язане з регресійним аналізом, тому його часто називають кореляційно-регресійним. Головними завданнями кореляційного аналізу є: – визначення форми зв'язку; – вимірювання щільності (сили) зв'язку; – виявлення впливу факторів на результативну ознаку. Здійснення кореляційного аналізу передбачає такі послідовні етапи: 1) встановлення причинно-наслідкових зв'язків між досліджуваними ознаками (виявлення факторів та вибір серед них тих, які найбільше впливають на результативний показник); 2) формування кореляційно-регресійної моделі (інформаційне забезпечення аналізу, вибір типу і форми зв'язку, складання моделі); 3) визначення кореляційних характеристик (показників зв'язку); 4) статистична оцінка параметрів зв'язку (економічна інтерпретація, оцінка значимості коефіцієнтів кореляції (наскільки відібрані фактори пояснюють варіацію результативного показника) та використання їх для вирішення практичних завдань, наприклад прийняття рішень, прогнозування, планування, нормування тощо (рис. 12.3). Отже, на початковому етапі аналізу виявляються зв'язки між результативною і факторними ознаками. Ці зв'язки можуть бути різними залежно від характеру залежності, напряму дії та аналітичного виразу (рис. 12.4).
Рис. 12.3. Схема кореляційно-регресійного аналізу На другому етапі оцінюється вихідна інформація для дослідження з використанням різних статистичних критеріїв (середнє квадратичне відхилення, коефіцієнт варіації тощо), а потім формується модель стохастичного зв'язку. Для здійснення кореляційного аналізу скористаємося прикладом, який використали раніше для демонстрації регресійного аналізу. Спочатку оцінимо типовість та однорідність даних спостереження, які визначаються відносним їх розподілом навколо середнього рівня, за допомогою таких критеріїв, як середньоквадратичне відхилення (а) та коефіцієнт варіації (V).
Рис. 12.4. Види зв'язків суспільних явищ Хоча варіація факторної ознаки і велика, проте вона не перевищує 33%. Це означає, що вихідні дані можна оцінити як однорідні та використати в подальших дослідженнях. Вважається, якщо варіація вище 33% – це свідчить про неоднорідність сукупності та потребує виключення нетипових матеріалів спостереження, як правило, в перших та останніх ран-жованих рядах вибірки. Незначною визнається варіація, що не перевищує 10% (табл. 12.4). Формування кореляційної моделі передбачає визначення чи це буде проста (парна) кореляція (результативна ознака з одним фактором), чи множинна (результативна ознака і декілька факторів). У свою чергу за характером зв'язку кореляційні моделі можуть бути лінійними (прямолінійними, з оберненою лінійною залежністю) чи нелінійними (криволінійними). Таблиця 12.4. Оцінка варіації за коефіцієнтом варіації
У лінійних моделях тіснота зв'язку між досліджуваними показниками вимірюється за допомогою лінійного коефіцієнта кореляції (Пірсона) r за формулою При цьому: Коефіцієнт кореляції набуває значень у межах ±1, завдяки чому відображає не лише щільність (тісноту) зв'язку, а й його напрям. Так, додатне значення свідчить про наявність прямого зв'язку, а від'ємне – зворотного. Розрахуємо коефіцієнт кореляції: Отже, розрахований коефіцієнт кореляції свідчить про наявність значного зв'язку між рівнем озброєності праці основними засобами та продуктивністю праці. Оскільки обчислений коефіцієнт кореляції більший за критичне його значення (0,6 > 0,3809), то з вірогідністю 0,95 можна стверджувати про статистично достовірну залежність між озброєністю і продуктивністю праці. Шкала оцінки тісноти зв'язку за коефіцієнтом кореляції та критичне його значення наведені в табл. 12.5 і 12.6. Таблиця 12.5. Величина коефіцієнта кореляції і тіснота зв'язку за "Таблицею Чеддока"
Крім відображення щільності зв'язку, коефіцієнт кореляції відіграє ще одну важливу роль – через коефіцієнт детермінації (D) він характеризує розмір впливу факторів на результативну ознаку: Таблиця 12.6. Критичне значення коефіцієнта кореляції
У нашому прикладі Це означає, що у наведеному прикладі 36% рівня продуктивності праці формується під впливом озброєності працівників основними засобами. Решту 64% становлять інші фактори – матеріальна зацікавленість робітників, інтенсивність використання робочого часу тощо. Залежності між декількома факторними ознаками складніші q виражаються рівнянням множинної лінійної кореляції Коефіцієнт множинної кореляції характеризує ступінь тісноти зв'язку між залежною змінною та кількома незалежними змінними. Він не може бути меншим, ніж абсолютна величина будь-якого коефіцієнта парної чи множинної кореляції і набуває значення від 0 до 1. Загальний математичний вираз коефіцієнта множинної кореляції має вигляд де де Рівняння множинної регресії і показники множинної кореляції розв'язують і визначають за допомогою спеціальних комп'ютерних програм. Таким чином, кореляційний аналіз має велике значення в економічному аналізі, вивченні суспільних явищ і процесів. Зокрема, він допомагає вирішити такі завдання: – встановлення характеру і тісноти зв'язку між досліджуваними явищами; – кількісний вимір ступеня впливу окремих факторів та їх сукупності на рівень явища, яке вивчається; – розрахунок кількісних змін аналізованого явища при прогнозуванні показників та об'єктивна оцінка господарської діяльності підприємства. Велике значення відводиться кореляційному аналізу в дослідженні кореляційних зв'язків на виробництві, зокрема між рівнем продуктивності праці та озброєністю її основними засобами, між урожайністю і кількістю внесених добрив, між собівартістю і випуском продукції та ін. Завдяки кореляційному аналізу є можливість глибше дослідити взаємозв'язки економічних явищ і процесів, виявити вплив факторів на результати господарської діяльності, виявити і підрахувати резерви підвищення ефективності виробництва. Все це позитивно позначається на здійсненні управлінської, маркетингової та інших видів діяльності, прийнятті економічно обґрунтованих господарських рішень. Кластерний аналіз Кластерний аналіз з'явився порівняно недавно – у 1939 р. Його запропонував вчений К. Тріон. Дослівно термін "кластер" в перекладі з англійської "cluster" означає гроно, згусток, пучок, група. Особливо бурхливий розвиток кластерного аналізу відбувся у 60-х роках минулого століття. Передумовами цього були поява швидкісних комп'ютерів та визнання класифікацій фундаментальним методом наукових досліджень. Кластерний аналіз – це метод багатомірного статистичного дослідження, до якого належать збір даних, що містять інформацію про вибіркові об'єкт
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 914; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.142.42 (0.024 с.) |

 ) – це середній квадрат відхилень окремих значень ознак (х) від їх середньої величини. Вона обчислюється за формулою
) – це середній квадрат відхилень окремих значень ознак (х) від їх середньої величини. Вона обчислюється за формулою
 – загальна середня для всієї досліджуваної сукупності;
– загальна середня для всієї досліджуваної сукупності; ) є середнім квадратом відхилень варіантів ознаки (х) від групової середньої величини. Розраховується за формулою
) є середнім квадратом відхилень варіантів ознаки (х) від групової середньої величини. Розраховується за формулою
 – групова середня;
– групова середня; ) визначається за формулою
) визначається за формулою
 ) або дисперсія групових середніх вимірює варіацію результативної ознаки за рахунок факторної ознаки, покладеної в основу групування. Її формула
) або дисперсія групових середніх вимірює варіацію результативної ознаки за рахунок факторної ознаки, покладеної в основу групування. Її формула
 .
. ;
2) середній квадрат варіантів ознаки
;
2) середній квадрат варіантів ознаки
 ;
3) загальну дисперсію
;
3) загальну дисперсію
 .
.
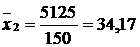 ;
2) середній квадрат варіантів ознаки
;
2) середній квадрат варіантів ознаки
 ;
3) загальну дисперсію =1179,17-
;
3) загальну дисперсію =1179,17-
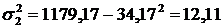 .
.
 .
. .
. .
. .
. , або 80,5%.
, або 80,5%.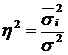
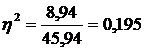 , або 19,5%.
, або 19,5%. .
. .
. ,
, ,
,  – число ступенів свободи;
– число ступенів свободи; ;
;  .
. .
. ) під впливом зміни факторних ознак (хі).
) під впливом зміни факторних ознак (хі). ,
, ,
, – вільний член рівняння;
– вільний член рівняння; – коефіцієнт регресії;
– коефіцієнт регресії;

 , або
, або 




 .
. .
. .
.
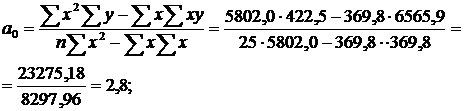

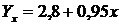 .
. , що відповідає середньому рівню продуктивності праці (табл. 12.3).
, що відповідає середньому рівню продуктивності праці (табл. 12.3).
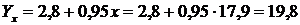 .
. .
. ,
, – коефіцієнти регресії;
– коефіцієнти регресії; – незалежні змінні (факторні ознаки);
– незалежні змінні (факторні ознаки);

 ;
;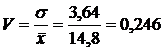 , або 24,6%.
, або 24,6%. .
.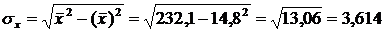 ;
; .
. .
. .
. .
. .
.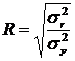 ,
, – теоретична (відтворена) варіація – дисперсія значень величини у, розрахованих шляхом підстановки значень факторів у знайдене рівняння регресії
– теоретична (відтворена) варіація – дисперсія значень величини у, розрахованих шляхом підстановки значень факторів у знайдене рівняння регресії ,
, – загальна варіація – дисперсія фактичних значень величини у.
– загальна варіація – дисперсія фактичних значень величини у.


