
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Методи обробки економічної інформаціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Тема 4. Методи обробки економічної інформації 1. Сутність методу і методики в економічному аналізі; 2. ТРАДИЦІЙНІ МЕТОДИ ОБРОБКИ ЕКОНОМІЧНОЇ ІНФОРМАЦІЇ 3. МЕТОДИ ДЕТЕРМІНОВАНОГО ФАКТОРНОГО АНАЛІЗУ 4. Методи стохастичного факторного аналізу. 1. Сутність методу і методики в економічному аналізі; В економічному аналізі метод – це сукупність способів, прийомів, операцій практичного і теоретичного характеру з вивчення економічних процесів, підпорядкованих досягненню основної мети – підвищенню ефективності господарювання економічних суб'єктів. Отже, метод – це спосіб, інструмент досягнення мети і завдань дослідження, який показує, яким чином можна провести дослідження і зробити на основі отриманих результатів обґрунтовані висновки й пропозиції. Загальною основою розробки і застосування аналітичної методології є принципи діалектичного підходу до вивчення економічних явищ і процесів. По-перше, це вимога розгляду фактів, що характеризують досліджуване явище в цілому, у взаємозв'язку і взаємообумовленості, що дуже важливо при вивченні причинних залежностей і визначенні невикористаних резервів підвищення ефективності господарювання. По-друге, важливим діалектичним методом пізнання є розгляд досліджуваного явища у розвитку, русі від виникнення до зникнення, що сприяє вивченню динаміки економічних явищ в їх історичній обумовленості. Історичний метод дає змогу дослідити виникнення, формування і розвиток економічних, господарських процесів та подій у хронологічному порядку, що сприяє виявленню внутрішніх і зовнішніх зв'язків, закономірностей, суперечностей. Класифікація та сфера використання методів дослідження
Існує кілька рівнів класифікацій методів економічного аналізу. Перший рівень класифікації виділяє неформалізовані та формалізовані методи аналізу. Неформалізовані методи ґрунтуються на описі аналітичних процедур на логічному рівні, а не на чітких аналітичних залежностях. До них відносяться методи: експертних оцінок, сценаріїв, психологічні, морфологічні, порівняння, побудови систем показників, побудови систем аналітичних таблиць тощо. Застосування цих методів характеризується певним суб'єктивізмом, оскільки велике значення мають інтуїція, досвід та знання аналітика. До формалізованих методів відносяться методи, в основі яких лежать досить чіткі формалізовані аналітичні залежності. Відомі десятки цих методів; вони складають другий рівень класифікації. Класичні методи аналізу господарської діяльності та фінансового аналізу: ланцюгових підстановок, арифметичних різниць, балансовий, виділення ізольованого впливу факторів, відсоткових чисел, диференціальний, логарифмічний, інтегральний, простих і складних відсотків, дисконтування тощо. Традиційні методи економічної статистики: середніх і відносних величин, групування, графічний, індексний та елементарні методи обробки рядів динаміки. Математично-статистичні методи вивчення зв'язків: кореляційний аналіз, регресійний аналіз, дисперсійний аналіз, факторний аналіз, метод головних компонентів, кореляційний аналіз, метод об'єкто-періодів, кластерний аналіз та ін. методи. Економетричні методи: матричні методи, спектральний аналіз, методи теорії виробничих функцій, теорії міжгалузевого балансу. Методи економічної кібернетики й оптимального програмування: методи системного аналізу, методи машинної імітації, лінійне програмування, нелінійне програмування, динамічне програмування тощо. Методи дослідження операиій і теорії прийняття рішень: методи теорії графів, метод дерев, теорія ігор, теорія масового обслуговування, методи сітьового планування й управління. З метою дослідження причинно-наслідкових зв'язків проводять логіко-інформаційне моделювання економічних явищ і процесів. Це дає змогу отримати чітке уявлення про досліджуваний об'єкт, кількісно описати, дати якісну характеристику його внутрішньої структури та зовнішніх зв'язків. Процес моделювання полягає у розробленні економіко-математичної конструкції досліджуваного обєкта на підставі визначення й опису його суттєвих характеристик (логічно, графічно, алгоритмами функцій і рівнянь), теоретичного аналізу моделі та їх порівняння з об^єктом, що реально функціонує. Цей процес умовно поділяють на три етапи. Перший етап - аналіз теоретичних закономірностей, властивих досліджуваному об'єкту, та емпіричних даних про його структуру й особливості. Для цього етапу характерне формування кінцевої мети побудови моделі та вибір критерію порівняння рішень. Другий етап - вибір найраціональніший. метод розв'язку аналітичної задачі. Найкраща модель та, яка дає змогу отримати най-раціональніше розв'язання та точніші економічні оцінки. Третій етап моделювання - всебічний аналіз результатів, одержаних при дослідженні економічних явищ і процесів. Критерієм достовірності та якості моделей є практична дієвість висновків і пропозицій. Моделювання факторних систем грунтується на основних критеріях виділення факторів як елементів цих систем: причинності, достатньої специфіки, самостійності існування, облікової можливості. Для формалізації аналітичної моделі вони повинні мати кількісне вираження. При моделюванні детермінованих функціональних звчязків в економічному аналізі виділяють такі види моделей. 1. Адитивні моделі – сума показників. Прикладами таких моделей є зведені витрати на виробництво за сумою елементів цих витрат, баланс продажу продукції, баланс робочого часу робітника. 2. Мультиплікативні моделі – добуток. 2. ТРАДИЦІЙНІ МЕТОДИ ОБРОБКИ ЕКОНОМІЧНОЇ ІНФОРМАЦІЇ Індексний метод Дослівно індекс (index) перекладається з латинської як "показник". Індекс – це відносна величина, за допомогою якої можна порівнювати окремі показники однорідного об'єкта та складні економічні явища, утворені з різнорідних елементів, що не підлягають безпосередньому підсумовуванню. Індивідуальний індекс (простий, частковий) – це результат порівняння двох показників, які належать однорідному об'єкту (наприклад, цін якогось товару, обсягів його реалізації, кількості виробленої продукції у звітному і базисному періодах тощо). В індивідуальних індексах досліджувана ознака береться без урахування зв'язку її з іншими ознаками явища, що вивчається. Наприклад, індивідуальний індекс ціни має вигляд а фізичного обсягу де Метод різниць. До методу різниць належать прийоми ланцюгових підстановок, абсолютних (арифметичних) різниць та відносних (процентних) різниць. Прийом ланцюгових підстановок по праву вважається основним прийомом елімінування. Він використовується в дослідженні функціональних залежностей і призначений для виміру впливу зміни факторних ознак на зміну результативного показника за незмінного (фіксованого) значення інших. Для цього послідовно замінюються базисні значення кожного фактора (планові, минулого періоду) на фактичні його дані (звітні). Отримані результати почергової заміни кожного фактора-показника порівнюються. Різниця між кожним наступним і попереднім показниками характеризуватиме вплив фактора, за умови усунення впливу всіх інших чинників. Ґрунтуючись на викладеному вище, прийом ланцюгових підстановок часто називають прийомом послідовного, поступового ізолювання факторів. При застосуванні прийому ланцюгових підстановок слід дотримуватися чіткого порядку заміни факторів: – у першу чергу замінюються об'ємні (кількісні) показники; – у другу – структурні; – у третю – якісні. У випадках, коли в аналітичній моделі є декілька кількісних чи якісних показників, серед них встановлюють черговість – спочатку замінюють основні, первинні (загальні) показники, а потім – вторинні, похідні Загальну схему прийому ланцюгових підстановок розглянемо на прикладі чотирьохфакторної мультиплікативної моделі: де Т – результативний показник; а, Ь, с, d – факторні показники, причому а – якісний показник; в – структурний показник; с, d – об'ємні (кількісні) показники і показник d первинний щодо показника с. Порівняємо фактичні значення показників (індекс "1") з плановими (індекс "0"). Повне відхилення показника Т від плану становитиме: де Для проведення подальших розрахунків перебудуємо нашу аналітичну модель в порядку необхідному для здійснення заміни показників. Тоді: Визначимо варіацію результативного показника, обумовлену зміною усіх факторів і кожного окремо: Таким чином: Метод абсолютних різниць є частковим вираженням методу ланцюгових підстановок і використовується під час дослідження детермінованих залежностей мультиплікативного типу. Щоб визначити вплив кількісного фактора, треба його абсолютне відхилення помножити на базове значення якісного; щоб визначити вплив якісного – його абсолютне відхилення помножити на базове значення кількісного.
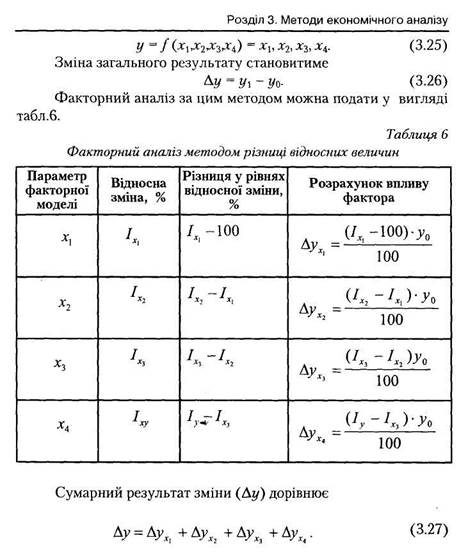
Метод різниці відносних величин - логічний прийом, який дає змогу виділити з сукупності факторів вплив одного, якщо існує детермінована факторна модель функціонального зв'язку, а значення впливу факторів виражені відносними величинами зміни. Для кожного аналізованого фактора послідовно визначають різницю в рівнях його впливу і впливу попереднього фактора, а отриманий результат треба помножити на абсолютне базове значення досліджуваного параметра зміни. Ця величина є кількісним результатом впливу цього фактора і його часткою у результаті сукупного впливу дії всіх факторів.Варто враховувати, що вплив останнього фактора визначають як різницю у рівнях відносної зміни загального результату і передостаннього фактора. Наприклад, загальний результат - обсяг виробленої продукції (У), можна подати як детерміновану факторну модель зв’язку з кількістю робітників (Х1), середнім числом відпрацьованих ними у році днів (Х2), середньою тривалістю робочого дня (Х3) і середньогодинним виробітком (Х4) у вигляді:
Застосування інтегрального методу аналізу обумовлено тим, що розглянуті вище прийоми абсолютних, відносних різниць, ланцюгових підстановок мають певні недоліки (про які сказано вище), що знижує об'єктивність оцінок. Інтегральний метод точніший. Він придатний для застосування як для мультиплікативних, так і для кратних і комбінованих моделей. Сутність інтегрального методу полягає у розкладанні абсолютного відхилення (приросту) результативного показника на окремі показники-фактори з урахуванням взаємозв'язку між ними. Способи розрахунку відповідних показників залежать від типу факторної моделі. Мультиплікативні моделі. 1. Двохфакторна мультиплікативна модель типу Для вимірювання впливу факторів використовуються такі формули: д a, b – фактори; Т – результативний показник; D – відхилення фактичних (звітних) даних від базисних (планових, минулого року) за досліджуваними показниками. Покажемо методику застосування інтегрального методу у двофакторній моделі, використовуючи дані табл. 11.5. Визначити інтегральним методом вплив зміни кількості виробленої продукції та її собівартості на загальні витрати виробництва: 1) розрахуємо вплив зміни обсягу виробництва на витрати виробництва: 2) розрахуємо вплив зміни собівартості на витрати виробництва: Баланс відхилень: 2. Трьохфакторна мультиплікативна модель типу Т = abc. Приклад. Інтегральним методом визначити вплив факторів на зміну випуску продукції (табл. 11.6): Таблиця 11.6. Випуск продукції, кількість та продуктивність праці робітників
1) вплив зміни середньорічної чисельності робітників на випуск продукції: 2) вплив зміни середньорічної кількості відпрацьованих днів на випуск продукції: 3) вплив зміни середньоденного виробітку на випуск продукції: Баланс відхилень: Отже, у звітному році, порівняно з попереднім, випуск продукції збільшився на 554, 4 тис. грн. Збільшення чисельності працівників сприяло зростанню випуску продукції на 293 860 грн. Проте скорочення кількості відпрацьованих днів спричинило падіння випуску на 67 900 грн. Позитивно вплинула на випуск продукції зміна середньоденної продуктивності праці, завдяки чому випуск зріс на 328 440 грн. 3. Чотирифакторна мультиплікативна модель типу Т = abcd. ПРИКЛАД. Інтегральним методом визначити вплив зміни факторів на результативний показник, використовуючи дані табл.11.5: 1) загальна зміна випуску продукції. 2) зміна випуску продукції за рахунок зміни чисельності робітників: 3) зміна випуску продукції за рахунок зміни кількості відпрацьованих днів: 4) зміна випуску продукції під впливом динаміки тривалості зміни: 5) вплив середньогодинного виробітку на випуск продукції:
Баланс відхилень: 4. Кратна модель типу Вплив факторів на результативний показник визначається таким чином: 5. Комбінована модель типи Для розрахунку динаміки зміни результативного показника зі зміною факторних необхідно скористатися такими формулами Дисперсійний аналіз Дисперсія (лат. dispersio – розсіювання) часто застосовується в теорії ймовірностей і математичній статистиці. Означає ступінь розсіювання навколо середнього значення випадкової величини. У статистичному розумінні дисперсія є середнє арифметичне із квадратів відхилень величин від їх середнього арифметичного. На практиці при проведенні аналізу економічного стану підприємства чи галузі часто необхідно оцінити розсіювання можливих значень випадкової величини навколо її середнього значення, а також виявити та виміряти силу зв'язку між факторними та результативною ознаками. Дисперсійний аналіз – це статистичний метод, призначений для встановлення структури зв'язку між результативною та факторними ознаками. Він дає змогу визначити вплив одного або декількох факторів на результативний показник. Дисперсійний аналіз може застосовуватися за обмеженої кількості одиниць спостереження. До того ж він особливо ефективний в умовах, коли результативна ознака суттєво змінюється під одночасною дією кількох факторів з неоднаковою силою впливу. Дисперсійний метод аналізу відіграє велику роль в економічних дослідженнях завдяки тому, що він має самостійне значення. Завдяки цьому методу вирішуються такі завдання: – кількісне вимірювання сили впливу факторних ознак та їх сполучень на результативну; – оцінка вірогідності впливу та його довірчих меж; – аналіз окремих середніх і статистична оцінка їх різниці. Крім того, у поглибленому аналізі дисперсійний метод може виконувати допоміжні функції, які дають змогу обґрунтовано використовувати інші методи аналізу. Розв'язання задачі виміру зв'язку спирається на розкладення суми квадратів відхилень досліджуваних значень результативної ознаки від загальної середньої на окремі частини, які обумовлюють зміну цієї ознаки. Якщо сукупність розбита на групи, то при цьому розраховуються загальна, групова, середня з групових і міжгрупова дисперсії. Загальна дисперсія ( де f – обсяг сукупності (кількість одиниць). Загальна дисперсія відображає варіацію досліджуваної ознаки за рахунок усіх умов, які впливають на неї у цій сукупності. Групова дисперсія ( де і – порядковий номер х та f в межах групи. Групова дисперсія характеризує варіацію ознаки в межах групи за рахунок всіх інших факторів за виключенням того, який покладений в основу групування. Щоб виміряти таку варіацію для сукупності в цілому, необхідно знайти середню із групових дисперсій. Середня з групових дисперсій ( Середня з групових дисперсій характеризує випадкову варіацію в кожній окремій групі. Ця варіація виникає під впливом інших факторів, що не враховуються, і не залежить від ознаки-фактора, покладеної в основу групування. Міжгрупова дисперсія ( Приклад. За даними табл. 12.1 зробити дисперсійний аналіз варіації урожайності озимої пшениці за двома виробничими підрозділами. При цьому другий підрозділ вніс мінеральні добрива, а перший – ні. Таблиця 12.1. Посівні площі та урожайність озимої пшениці в господарстві за двома виробничими підрозділами
Розрахуємо спочатку середню врожайність по господарству: Далі визначаємо:
Визначимо середню з групових дисперсій як середню арифметичну зважену із групових дисперсій: Знайдемо міжгрупову дисперсію: Тоді загальна дисперсія за урожайністю озимих зернових становитиме: Отже, про зв'язок між досліджуваними ознаками можна судити за допомогою коефіцієнта детермінації, який є відношенням міжгрупової дисперсії до загальної і записується у вигляді формули Коефіцієнт детермінації показує ступінь участі факторної ознаки у формуванні загальної змінюваності результативної ознаки. Зокрема, щодо нашого прикладу ступінь впливу кількості внесених добрив на урожайність зернових становить 80,5%: Ступінь впливу інших неврахованих факторів на результативну ознаку обчислюють за співвідношенням Рівень впливу інших неврахованих чинників дорівнює 19,5%. Проте найчастіше в економічному аналізі в ролі показника тісноти зв'язку застосовується кореляційне відношення (емпіричне), яке є коренем другого ступеня із коефіцієнта детермінації. Формула його така: У нашому прикладі Це свідчить про те, що мінеральні добрива суттєво впливають на урожайність озимої пшениці. Для підтвердження істотності зв'язку використаємо критерій Фішера де n – число одиниць сукупності; m – кількість груп. Отже, За допомогою таблиці критичних значень F-критерію порівняємо отриманий критерій із критичним значенням для рівня ймовірності 0,95. Для рівня значимості а = 0,05 табличне значення не перевищує 2,99. Оскільки розраховане значення критерію Фішера більше критичного (922,7 > 2,99), то це підтверджує істотність зв'язку між кількістю внесених добрив і урожайністю озимої пшениці. Регресійний аналіз Під терміном " регресія " розуміють рух назад, повернення до попереднього стану. Названий термін ввів у кінці XIX ст. Френсіс Галтон. В результаті проведеного ним дослідження зв'язку між зростом батьків і дітей, виявилося, що наявна обернена залежність. Так, у батьків з дуже високим зростом діти мають менший зріст порівняно з середнім зростом батьків. І, навпаки, у дуже низьких батьків середній зріст дітей вищий. В одному і другому випадку середній зріст дітей прямує (повертається) до середнього зросту населення певної місцевості. Саме такою залежністю і пояснюють вибір терміна "регресія". Регресійний аналіз (англ. regression analysis) – це метод визначення відокремленого і спільного впливу факторів на результативну ознаку та кількісної оцінки цього впливу шляхом використання відповідних критеріїв. Регресійний аналіз проводиться на основі побудованого рівняння регресії і визначає внесок кожної незалежної змінної у варіацію досліджуваної (прогнозованої) залежної змінної величини. Основним завданням регресійного аналізу є визначення впливу факторів на результативний показник (в абсолютних показниках). Передусім для цього необхідно підібрати та обґрунтувати рівняння зв'язку, що відповідає характеру аналітичної стохастичної залежності між досліджуваними ознаками. Рівняння регресії показує як в середньому змінюється результативна ознака ( У загальному вигляді рівняння регресії можна представити так: де х – незалежні змінні величини (фактори). Залежно від кількості змінних величин виділяють різні види регресійного аналізу. Якщо змінна величина завжди одна, то змінних може бути як одна, так і декілька. Виходячи з цього, виділяють два види регресійного аналізу: парний (простий) регресійний аналіз і регресійний аналіз на основі множинної регресії, або багатофакторний. Парний регресійний аналіз – вид регресійного аналізу, що включає у себе розгляд однієї незалежної змінної величини, а багатофакторний – відповідно дві величини і більше. Зважаючи на характер зв'язку, в регресійному аналізі можуть використовуватися лінійні та нелінійні функції. Для визначення характеру залежності та, відповідно, побудови рівняння регресії доцільно застосувати графічний метод, порівняння рівнобіжних рядів вихідних даних, табличний метод. Так, графічний метод дає найбільш наочну картину розміщення крапок на графіку, завдяки чому можна виявити напрям і вид залежності між досліджуваними показниками: прямолінійна чи криволінійна. За допомогою порівняння рівнобіжних рядів ознак можна спостерігати за рівномірністю їх взаємних змін. Якщо зміна факторної ознаки (х) призводить до відносно рівномірної зміни результативної ( Найпростішим рівнянням парної регресії, що описує лінійну залежність між факторною і результативною ознаками, є рівняння прямої, яке має такий вигляд: де х – незалежна змінна (факторна ознака), яка використовується для визначення залежної змінної. Параметри рівняння обчислюються на основі системи нормальних рівнянь методом найменших квадратів: Звідси Для зручності розрахунків регресійного та кореляційного аналізу (розглянемо далі) доцільно використати таку форму таблиці (табл. 12.2). Таблиця 12.2. Вихідні та розрахункові дані для обчислення регресійно-кореляційних характеристик (парна прямолінійна кореляція)
Основне змістовне навантаження в рівнянні регресії несе коефіцієнт регресії. Найчастіше застосовуються лінійні рівняння або приведені до лінійного вигляду. Коефіцієнт регресії – це кутовий коефіцієнт у прямолінійному рівнянні кореляційного зв'язку. У лінійній функції рівняння регресії він показує на скільки одиниць в середньому зміниться результативна ознака (у) при зміні факторної ознаки (х) на одиницю свого натурального виміру. Тобто, коефіцієнт регресії – це варіація у, яка припадає на одиницю варіації х. Коефіцієнт регресії має одиницю виміру результативної ознаки. За наявності прямого зв'язку коефіцієнт регресії є додатною величиною, а за зворотного зв'язку – від'ємною. Параметр а0 – вільний член рівняння регресії, тобто це значення у при х=0. Цей показник має тільки розрахункове значення у випадках, коли х не має нульових значень. У разі, коли зі зміною факторної ознаки результативна змінюється нерівномірно, використовуються нелінійні функції. Так, якщо зміна факторного показника сприяла прискореній динаміці результативного показника (наприклад, вплив обсягу грошової маси на рівень інфляції), доцільно використати степеневу функцію: У випадку, коли під впливом факторної ознаки результативна змінюється нерівномірно, причому з уповільненням, використовується рівняння гіперболи: Прикладом такої залежності є залежність рівня продуктивності праці робітників від рівня їх заробітної плати. Якщо зміна факторної ознаки супроводжується нерівномірною варіацією факторної ознаки із зміною напряму зв'язку, нелінійна регресія описується рівнянням параболи: Так, за допомогою функції параболи можна виразити залежність урожайності культур від кількості опадів. Приклад. За даними 25 заводів дослідити залежність між рівнями озброєності праці основними засобами та її продуктивністю, використовуючи регресійний аналіз (табл. 12.3). Таблиця 12.3. Озброєність праці основними засобами та рівень її продуктивності в групі заводів України, тис. грн
|

 ,
, ,
, – ціна одиниці товару у звітному періоді, грн;
– ціна одиниці товару у звітному періоді, грн; – ціна одиниці товару у базисному періоді, грн;
– ціна одиниці товару у базисному періоді, грн; – кількість проданих товарів у звітному періоді, од.;
– кількість проданих товарів у звітному періоді, од.; – кількість проданих товарів у базисному періоді, од.
– кількість проданих товарів у базисному періоді, од.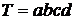 ,
, ,
,
 .
.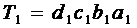 ;
;  .
. – загальний вплив факторів;
– загальний вплив факторів;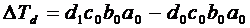 – вплив фактора d;
– вплив фактора d; – вплив фактора с;
– вплив фактора с; – вплив фактора b;
– вплив фактора b; – вплив фактора а;
– вплив фактора а;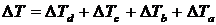 .
.
 .
. ;
;  ;
; (грн);
(грн); (грн).
(грн).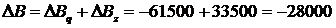 (грн).
(грн). ;
;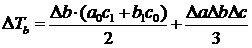 ;
; .
.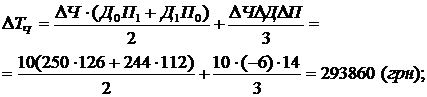








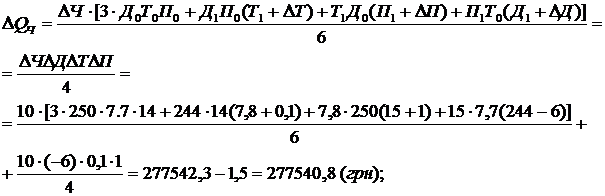


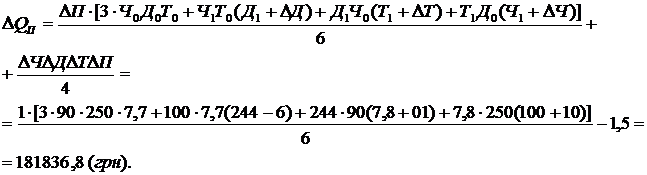

 .
.

 .
.


 ) – це середній квадрат відхилень окремих значень ознак (х) від їх середньої величини. Вона обчислюється за формулою
) – це середній квадрат відхилень окремих значень ознак (х) від їх середньої величини. Вона обчислюється за формулою
 – загальна середня для всієї досліджуваної сукупності;
– загальна середня для всієї досліджуваної сукупності; ) є середнім квадратом відхилень варіантів ознаки (х) від групової середньої величини. Розраховується за формулою
) є середнім квадратом відхилень варіантів ознаки (х) від групової середньої величини. Розраховується за формулою
 – групова середня;
– групова середня; ) визначається за формулою
) визначається за формулою
 ) або дисперсія групових середніх вимірює варіацію результативної ознаки за рахунок факторної ознаки, покладеної в основу групування. Її формула
) або дисперсія групових середніх вимірює варіацію результативної ознаки за рахунок факторної ознаки, покладеної в основу групування. Її формула
 .
. ;
2) середній квадрат варіантів ознаки
;
2) середній квадрат варіантів ознаки
 ;
3) загальну дисперсію
;
3) загальну дисперсію
 .
.
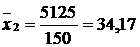 ;
2) середній квадрат варіантів ознаки
;
2) середній квадрат варіантів ознаки
 ;
3) загальну дисперсію =1179,17-
;
3) загальну дисперсію =1179,17-
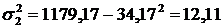 .
.
 .
. .
. .
. .
. , або 80,5%.
, або 80,5%.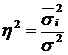
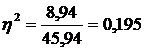 , або 19,5%.
, або 19,5%. .
. .
. ,
, ,
,  – число ступенів свободи;
– число ступенів свободи; ;
;  .
. .
.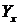 ) під впливом зміни факторних ознак (хі).
) під впливом зміни факторних ознак (хі). ,
, ,
, – вільний член рівняння;
– вільний член рівняння; – коефіцієнт регресії;
– коефіцієнт регресії;

 , або
, або 




 .
. .
. .
.


