
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи факторного аналізу, засновані на прийомі елімінуванняСодержание книги
Поиск на нашем сайте
Елімінування означає виключення, тобто при визначенні впливу визначеного фактора на результативний показник виключають вплив інших факторів. Це відбувається шляхом фіксування усіх факторів крім досліджуваного на одному рівні – базовому (плановому) чи фактичному. Досліджуваний фактор при цьому береться як той, що змінюється. Прийом елімінування застосовується в таких методах, як метод ланцюгових підстановок, метод абсолютних різниць, метод відносних різниць, метод переліченого плану, метод структурних змін, метод пайової участі, метод коректувань. Недолік прийому і відповідних методів у тім, що вони спотворюють дійсність, тому що в реальності усі фактори діють одночасно. Цього недоліку позбавлений інтегральний і логарифмічний спосіб, що побудований на іншому принципі. Порядок оцінки факторів із застосуванням методів елімінування: 1) першими оцінюються кількісні фактори, другими оцінюються фактори структури (якщо вони є), третіми оцінюються якісні фактори. 2) Якщо в аналізованій формулі кілька кількісних чи якісних факторів, то порядок оцінки визначається: a) по важливості показника b) по складності показника (першими аналізуються більш складні показники, а потім більш прості)
Методи елімінування Метод ланцюгових підстановок – це універсальний метод, застосовується для всіх типів моделей. Приклад: Нехай мається результативний показник П, що залежить від факторних a, b і с. Форма взаємозв'язку мультиплікативна Постановка задачі факторного аналізу: необхідно визначити абсолютну зміну аналізованого результативного показника в звітному періоді в порівнянні з базовим під впливом відповідних факторів. Введемо умовні позначки:
Абсолютна зміна аналізованого показника за рахунок відповідних факторів:
Таблиця 3.2 – Розрахунок впливу факторів на результат методом ланцюгових підстановок
Перевірка
Правило для методу ланцюгових підстановок: Для того, щоб визначити вплив відповідного фактора на результативний показник необхідно з наступної підстановки відняти попередню. Підстановка – це умовна величина, у якій значення аналізованого показника береться по факту, а значення інших факторів беруться за планом (за базовим періодом), якщо вплив цих факторів ще не проаналізовано, і по факту, якщо значення цих показників вже проаналізовано.
Прийом абсолютних різниць – застосовується тільки для моделей мультиплікативного виду, є наслідком з методу ланцюгових підстановок. Виведемо відповідні формули:
Правило: для того, щоб визначити абсолютну зміну результативного показника під вплива факторного необхідно абсолютну зміну аналізованого фактора помножити на значення інших факторних показників: планові, якщо ці фактори ще не аналізувалися, і фактичні, якщо ці фактори вже проаналізовані.
Метод відносних різниць
Цей метод можливо застосувати для моделей мультиплікативного, кратного та змішаного типу (виду П = (а – в)с). Принцип цього методу полягає у тому, що для визначення впливу факторів на результативний показник використовують не абсолютні значення факторних показників, а їх відносні значення, що значно скорочує обсяг розрахунків, порівняно з методом ланцюгових підстав. Принцип застосування методу єдиний для моделей усіх типів, але правила його застосування для моделей різних типів відрізняються. Застосування методу відносних різниць для моделей мультиплікативного типу
Виведемо формулу методу відносних різниць з формули методу ланцюгових підстав (таблиця)
Таким чином можемо вивести правило застосування методу для моделей мультиплікативного типу. Для того, щоб визначити вплив на результативний показник першого відповідно до порядку оцінки факторів необхідно базове (планове) значення результативного показника помножити на відносну зміну – коефіцієнт приросту (Іа –1) – відповідного факторного показника.
Для того, щоб визначити вплив другого, третього, (nго) фактору необхідно базове (планове) значення результативного показника помножити на добуток індексів зміни попередніх за порядком аналізу показників та на відносну зміну відповідного факторного показника. Застосування методу відносних різниць для моделей кратного типу. Для моделей типу П =
Для моделей у яких в – кількісний показник, а – якісний показник правило змінюється і відповідні формули аналізу мають вигляд:
Метод часткової участі
Метод застосовується для змішаних моделей типу П = Існує декілька варіантів застосування методу. Опишемо один з них.
Порядок розрахунків. Для аналізу ми маємо багатоступінчату модель, яку графічно можливо описати:
Рис. 3 - Графічна модель аналізу показника
У таких багаторівневих моделях, по-перше, визначають вплив складних показників на результативний ( Для останнього третього етапу визначають відносну зміну складних показників під впливом простих: (
Потім розраховують вплив простих показників на результативний:
6 Інтегральний спосіб Елімінування як спосіб детермінованого факторного аналізу має істотний недолік. При його використанні виходять з того, що фактори змінюються незалежно друг від друга. Насправді ж вони змінюються спільно, взаємозалежно і від цієї взаємодії виходить додатковий приріст результативного показника, що при застосуванні способів елімінування приєднується до одного з факторів, як правило до останнього. У зв'язку з цим величина впливу факторів на зміну результативного показника змінюється в залежності від місця, на яке поставлений той чи інший фактор у детермінованій моделі. У результаті цього величина впливу одного фактора перебільшується, а іншого - применшується, що викликає неоднозначність оцінки впливу факторів, особливо в тих випадках, коли додатковий приріст досить істотний. Щоб позбутися від цього недоліку, у детермінованому факторному аналізі використовується інтегральний метод, що застосовується для виміру впливу факторів у мультиплікативних, кратних і змішаних моделях. Використання цього способу дозволяє одержувати більш точні результати розрахунку впливу факторів у порівнянні зі способами ланцюгових підстановок, абсолютних і відносних різниць і уникнути неоднозначної оцінки впливу факторів тому, що в даному випадку результати не залежать від місця розташування факторів у моделі, а додатковий приріст результативного показника, що утворився від взаємодії факторів, розкладається між ними пропорційно ізольованому їх впливу на результативний показник.
В інтегральному методі користаються визначеними формулами. Приведемо основні з них для різних моделей.
1.
2.
3.
4.
5.
Спосіб логарифмування
Спосіб логарифмування застосовується для виміру впливу факторів у мультиплікативних моделях. Результат розрахунку не залежить від місця розташування факторів у моделі й у порівнянні з інтегральним методом забезпечується більш висока точність у розрахунках. За допомогою логарифмування результат спільної дії факторів розподіляється пропорційно частки ізольованого впливу кожного фактора на рівень результативного показника. У цьому його перевага, а недолік в обмеженості його застосування. Він застосовується тільки для моделей мультиплікативного типу.
При логарифмуванні використовуються не абсолютні прирости результативних показників, а індекси їхнього росту (зниження).
З формул випливає, що загальний приріст результативного показника розподіляється між факторами пропорційно відношенню логарифмів індексів факторних показників до логарифму індексу результативного показника. При цьому не має значення який логарифм застосовується натуральний або десятичний.
Наведемо приклади застосування методів факторного аналізу Оцінити абсолютну зміну обсягу випуску товарної продукції (Q) у звітному періоді порівняно з планом під впливом таких факторів, як: середньоспискова чисельність промислово-виробничого персоналу ( Таблиця 1 — Показники з праці
Для розв'язання задачі побудуємо аналітичну та графічну модель взаємозв'язку між результативними показником (Q) та факторними. Середньорічний виробіток одного працюючого (ПТ) можливо знайти як:
де ПТдн — середньоденна виробітка одного працюючого. Деталізуючи показник середньденної виробітки маємо:
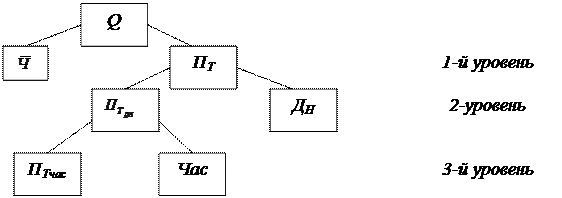
З формул (1), (2), (3) маємо таку залежність:
Графічна модель залежності результативного показника від факторних:
Отже маємо багаторівневу модель аналізу.
У моделі ми маємо 3 кількісних фактори та якісний ППча с — який згідно з правилом будемо оцінювати останнім. Для того, щоб визначити, який з кількісних факторів оцінювати першим застосуємо графічну модель, першими будемо оцінювати вплив факторів 1-го рівня, потім 2-го та 3-го. Перепишемо формулу (4) у відповідності до порядку оцінки факторів:
та застосуємо метод ланцюгових підстав. Оцінимо вплив зміни чисельності працівників (
Оцінимо вплив зміни кількості відпрацьованих днів (
Оцінимо вплив зміни кількості відпрацьованих за день годин (
Оцінимо вплив змін середньогодинного виробітку одного працюючого:
Зробимо перевірку:
Висновок: зростання обсягу виробництва товарної продукції було обумовлено ростом середньогодинного виробітку. Збільшення виробітку одного робітника на 0,099 грн. за годину могло б привести до зростання обсягу виробництва на 195, 652 тис. грн., якщо б не вплив інших факторів. Зниження середньоспискової чисельності працюючого на 4 особи викликало зменшення обсягу випуску на 17,123 тис. грн. Найбільш негативно вплинули на обсяг випуску такі фактори як кількість відпрацьованих одним робітником годин та днів. Під впливом зменшення кількості відпрацьованих днів на 8 днів обсяг виробництва знизився на 102, 896 тис. грн., а під впливом зменшення кількості часів, відпрацьованих у середньому 1 робітником за один день на 0,1 час обсяг виробництва зменшився на 49,733 тис. грн. Під сумісним впливом усіх чотирьох факторів у звітному періоді порівняно з плановим обсяг виробництва виріс на 25,9 тис. грн. Отже резервом росту обсягу виробництва є більш продуктивне використання робочого часу. Якби підприємство не припустило зростання внутрішньозмінних простоїв, та цілоденних простоїв, випуск продукції можливо було б збільшити на 152, 629 тис. грн. (49,733+102,896 тис. грн.), що до фактичного обсягу становить 3,93% приросту. Виконаємо аналіз з використанням методу відносних різниць.
= + 196,11 тис. грн.
Перевірка:
Ми бачимо, що результати розрахунків незначно відрізняються від попередніх. Неточність можна пояснити округленням індексів зміни показників.
Наведемо приклад застосування методу ланцюгових підстав у моделях кратного типу. Необхідно оцінити як вплинули на зміну рентабельності реалізованої продукції у звітному періоді порівняно за базовим такі фактори як виторг від реалізації та собівартість реалізованої продукції за такими вихідними даними:
Таблиця 2 — Аналіз рентабельності реалізованої продукції
Побудуємо аналітичну модель аналізу показника рентабельності. Рентабельність реалізованої продукції розраховується:
але оскільки П = В — С, маємо
По-перше оцінимо вплив собівартості, оскільки у процесі виробництво-реалізація, по-перше маємо витрати (собівартість), а по-друге, результати (виторг)
Оцінимо вплив зміни виторгу:
Перевіримо:
Висновок. У звітному періоді порівняно з базовим відбувається негативне явище — зниження рентабельності реалізованої продукції на 25,6%. Це обумовлено як зростанням собівартості продукції так і зниженням виторгу від реалізації. За рахунок зниження виторгу рентабельність знизилась на 20%, а за рахунок зростання собівартості знизилась на 5,6%. Для більш детального аналізу рентабельності необхідно з'ясувати фактори, які вплинули на зниження виторгу від реалізації та на зростання собівартості. Одним з недоліків, який притаманний усім методам факторного аналізу, які базуються на прийомі елімінування, є як ми вже зазначили необ'єктивний характер оцінки впливу факторів на результат. Розмір впливу факторів на результат буде залежати від порядку підстановки факторів. Доведемо це на прикладі. Нехай необхідно оцінити як вплинули на зміну середньорічного фонду оплати праці такі фактори як середньоспискова чисельність працівників та середньомісячна заробітна плата. Таблиця 3 — Аналіз оплати праці
Модель аналізу показника:
Застосуємо метод абсолютних різниць та два варіанти оцінки. У першому спочатку оцінимо вплив чисельності, а потім — заробітної плати. У другому варіанті — навпаки. Перший варіант. Вплив зміни чисельності працівників:
Вплив зміни середньої заробітної плати:
перевірка:
Другий варіант. Вплив зміни середньої заробітної плати:
Вплив зміни чисельності працівників:
Перевірка:
Таким чином ми бачимо, що обидва варіанти розрахунку дають вірну перевірку, але, як ми і стверджували, при різному порядку оцінки факторів маємо різні результати цієї оцінки. Для того, щоб усунути неточність розрахунків застосовують економіко-математичні методи аналізу такі як інтегральний та логаріфмічний. Розв'яжемо попереднє завдання із застосуванням логаріфмічного методу. Скористуємось формулою (8). Тоді маємо:
Перевірка
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.170.115 (0.01 с.) |

 . Нехай а – кількісний фактор, b – фактор структури, с – якісний фактор.
. Нехай а – кількісний фактор, b – фактор структури, с – якісний фактор. - значення показника за базовий чи плановий період
- значення показника за базовий чи плановий період (ф) - значення показника у фактичному періоді
(ф) - значення показника у фактичному періоді - абсолютна зміна показника
- абсолютна зміна показника - відносна зміна показника
- відносна зміна показника
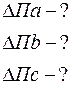

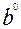

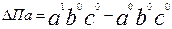






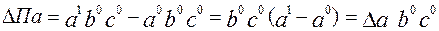








 , де а – кількісний показник, в – якісний показник, застосовують тіж самі правила, що і для мультиплікативних моделей:
, де а – кількісний показник, в – якісний показник, застосовують тіж самі правила, що і для мультиплікативних моделей: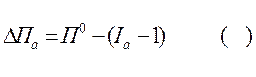
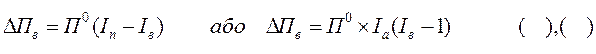
 (),()
(),() , де
, де  , тобто
, тобто 

 ); по-друге вплив простих факторів на складні (
); по-друге вплив простих факторів на складні (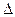 Аа;
Аа;  Аа;
Аа;  (), ()
(), () (), ()
(), () ()
()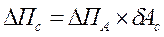 ()
() ()
() ()
()










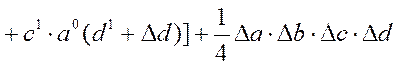



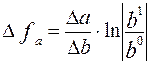




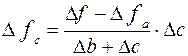
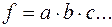


 ), середня кількість днів, відпрацьованих одним працівником за рік (ДН), середня кількість часів, відпрацьованих одним працівником за день (Час), середньочасова виробітка одного працюючого (ПП). Вихідні дані наведені у таблиці 1.
), середня кількість днів, відпрацьованих одним працівником за рік (ДН), середня кількість часів, відпрацьованих одним працівником за день (Час), середньочасова виробітка одного працюючого (ПП). Вихідні дані наведені у таблиці 1. ; або
; або  (1), (2)
(1), (2)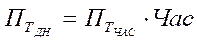 (3)
(3)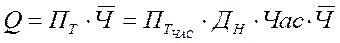 (4)
(4)
 (5)
(5) ):
):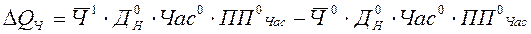 ()
() тис. грн.
тис. грн. ):
): ()
() тис. грн.
тис. грн. ):
): ()
() тис. грн.
тис. грн.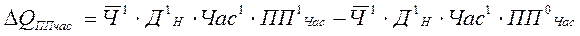 ()
() тис. грн.
тис. грн.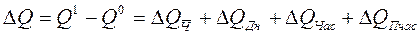 ()
() тис. грн.
тис. грн. тис. грн.
тис. грн. ()
() = 3850 * (0,99569 – 1) = -16,594 тис. грн.
= 3850 * (0,99569 – 1) = -16,594 тис. грн. (….)
(….)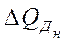 = 3850 * 0,99569 (0,97315 – 1) = -102,93 тис. грн.
= 3850 * 0,99569 (0,97315 – 1) = -102,93 тис. грн. ()
() = 3850 * 0,99569 * 0,97315 * (0,98667 – 1) = -49,73 тис. грн.
= 3850 * 0,99569 * 0,97315 * (0,98667 – 1) = -49,73 тис. грн. ()
() = 3850 * 0,99569 * 0,97315 * 0,98667 * (1,05328 – 1) =
= 3850 * 0,99569 * 0,97315 * 0,98667 * (1,05328 – 1) = = -16,594 + (-102,93) + (-49,73) + 196,11 = +26,856 тис. грн.
= -16,594 + (-102,93) + (-49,73) + 196,11 = +26,856 тис. грн. (6)
(6) (7)
(7)



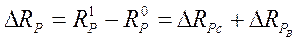

 (8)
(8) тис. грн.
тис. грн. тис. грн.
тис. грн. тис. грн.
тис. грн. тис. грн.
тис. грн. тис. грн.
тис. грн. тис. грн.
тис. грн.
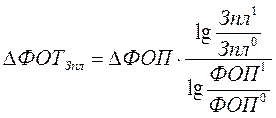
 тис. грн.
тис. грн. тис. грн.
тис. грн. тис. грн.
тис. грн.


