
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка лінійної регресії на адекватність (значимість) за допомогою f-критерію Фішера.Содержание книги
Поиск на нашем сайте При побудові на основі вибірки отримують вибіркову (випадкову) модель парної лінійної регресії. Перевірку її на значимість (адекватність) і перевірку значимості її коефіцієнтів здійснюється на основі перевірки статистичних гіпотез. Суть перевірки статистичних гіпотез: висувається (формується) початкова (нульова) гіпотеза Н0, а також альтернативна їй гіпотеза Н1. Вибирають деякий критерій, при цьому вважають, що він має один із статистичних способів розподілу випадкових величин, знаходять фактичне значення критерію. Потім за таблицями при заданому рівні значимості Якщо значення коефіцієнта детермінації Якщо Алгоритм перевірки 1. Формулюють статистичні гіпотези:
Якщо приймається нульова гіпотеза, тоді вважають, що побудована модель неадекватна дійсній. Якщо приймається альтернативна гіпотеза 2. Задають (вибирають) критерій:
Де 3. Задають рівень значимості Якщо рівень значимості 4. Знаходять фактичне значення критерію 5. Знаходять за таблицями розподілу Фішера критичне значення 6. Порівнюють між собою значення Якщо Якщо Зауваження: функція розподілу випадкової величини з розподілом Фішера має графік (графік).
Перевірка значимості параметрів регресійної моделі за допомогою t-критерію Ст’юдента Для перевірки на значимість параметрів регресійної моделі, при умові, що вона адекватна дійсній, потрібно спочатку знайти оцінку дисперсії залишків (помилок):
Тож потрібно знайти дисперсійно-коваріаційну матрицю параметрів моделей регресії:
Алгоритм перевірки значимості коефіцієнта лінійної регресії 1. Висувають статистичні гіпотези:
2. Задають критерій:
Вважають, що цей критерій має розподіл Ст’юдента (t-розподіл) з 3. Знаходять фактичне значення критерію 4. Знаходять за таблицями t-розподілу 5. Порівнюють між собою два знайдені значення. Якщо
Зауваження: функція розподілу Ст’юдента або t-розподілу має вигляд: (графік).
Перевірка значимості коефіцієнта кореляції за допомогою T-критерію Ст’юдента. Перевірка на значимість вибіркового коефіцієнта кореляції здійснюється за допомогою t-критерію Ст’юдента. Для перевірки вибирають критерій:
Вважають, що цей критерій має розподіл Ст’юдента з
Якщо приймається нульова гіпотеза, то вважають, що між змінними у та х не існує лінійної залежності. При гіпотезі Якщо отримана вибіркова модель лінійної регресії адекватна дійсній моделі, оцінки параметрів статистично значимі та між змінними х та у існує лінійний зв'язок, то цю вибіркову модель можна використати для дослідження процесу, який вона описує. Дослідження полягає в тому, щоб встановити рівень впливу, в певному розумінні, незалежної змінної на залежну, а також можливі значення різного типу прогнозованих значень у.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.201.71 (0.009 с.) |

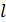 знаходять критичне значення критерію, який має такий самий закон розподілу. Порівнюють між собою отримані значення критерію і роблять наступний висновок: або приймається гіпотеза Н0 або альтернативна їй Н1.
знаходять критичне значення критерію, який має такий самий закон розподілу. Порівнюють між собою отримані значення критерію і роблять наступний висновок: або приймається гіпотеза Н0 або альтернативна їй Н1. або
або  , то тоді можна стверджувати про адекватність чи неадекватність побудованої моделі дійсній моделі.
, то тоді можна стверджувати про адекватність чи неадекватність побудованої моделі дійсній моделі. , тоді перевірку на адекватність здійснюють за допомогою F-критерію Фішера.
, тоді перевірку на адекватність здійснюють за допомогою F-критерію Фішера.
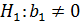
 , побудована модель адекватна дійсній.
, побудована модель адекватна дійсній.
 – кількість елементів у вибірці. Вважають, що даний критерій має розподіл Фішера з
– кількість елементів у вибірці. Вважають, що даний критерій має розподіл Фішера з  ступенями вільності (свободи).
ступенями вільності (свободи).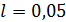 – це означає, що при прийнятті нульової гіпотези
– це означає, що при прийнятті нульової гіпотези  ми можемо помилитися не більше ніж в 5 випадках зі 100.
ми можемо помилитися не більше ніж в 5 випадках зі 100.
 для вибраного рівня значимості
для вибраного рівня значимості 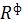 та
та  , тоді приймається нульова гіпотеза
, тоді приймається нульова гіпотеза 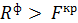 , нульова гіпотеза відкидається, приймається альтернативна гіпотеза
, нульова гіпотеза відкидається, приймається альтернативна гіпотеза 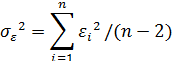
 називають стандартною помилкою рівняння регресії.
називають стандартною помилкою рівняння регресії.
 ,
,  - оцінки параметрів дисперсії
- оцінки параметрів дисперсії 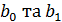
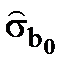 ,
,  - стандартні похибки коефіцієнтів
- стандартні похибки коефіцієнтів  (
( )
)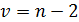
 (
( ).
). для рівня значимості
для рівня значимості  і
і  ступенів вільності.
ступенів вільності. (
( ) тоді приймається нульова гіпотеза і коефіцієнт
) тоді приймається нульова гіпотеза і коефіцієнт 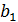 (
( ) вважається статистично не значимий, тобто його моделі можна опустити (відкинути). В противному випадку коефіцієнт
) вважається статистично не значимий, тобто його моделі можна опустити (відкинути). В противному випадку коефіцієнт 
 - вибіркова модель
- вибіркова модель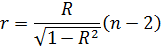
 ступенями вільності. Гіпотези мають вигляд:
ступенями вільності. Гіпотези мають вигляд:


