Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коефіцієнт еластичності. Довірчі інтервали (інтервали довіри). Прогнозування за допомогою моделі парної лінійної регресіїСодержание книги
Поиск на нашем сайте
Середнім коефіцієнтом еластичності моделі парної регресії називається величина:
Цей коефіцієнт показує на скільки процентів (відсотків) зміниться змінна у, якщо змінна х зміниться (збільшиться) на 1 процент (відсоток). Довірчі інтервали (інтервали довіри) Якщо для регресійної моделі Інтервал довіри (довірчий інтервал) – це інтервал, в який з ймовірністю Інтервали довіри мають вигляд:
(графік) Геометрична інтерпретація: Якщо полоса між прямими Прогнозування за допомогою моделі парної лінійної регресії Для регресійних моделей використовують в основному два типи прогнозів: точковий та інтервальний. Точковий прогноз – дає змогу знайти прогнозоване значення
Інтервальний прогноз задає інтервал, який з ймовірністю Інтервальний прогноз знаходиться наступним чином:
Нелінійна регресія В багатьох економетричних процесах лінійні економетричні моделі зручно використовувати для їх дослідження і прогнозування. Але значна кількість економічних процесів по своїй суті не є лінійними, тобто показники (фактори), які описують такі процеси пов’язані між собою нелінійними залежностями. Наприклад, описання виробничого процесу за допомогою функції Кобба-Дугласа. Розглянемо найпростіші нелінійні економітричні моделі, які можна звести за допомогою певних перетворень до лінійних економетричних моделей. 1. Логарифмічні моделі (log-моделі) До таких моделей належать моделі, в яких залежність між двома показниками має вигляд:
(графіки) Ця модель описує залежність між попитом на деякі товари від доходу, коли Модель (1) зводиться до лінійної шляхом логарифмування:
Отримаємо лінійну модель
Зауваження: економетрична логарифмічна модель має вигляд
2. Економетричні моделі типу виробничих функцій Виробнича функція – економетрична модель, яка кількісно описує зв'язок основних результативних показників виробничо-господарської діяльності з факторами, які впливають на ці показники. Найпростіша економетрична модель типу виробничої функції має вигляд:
Якщо Якщо Якщо До лінійно економетричної моделі зведення відбувається логарифмуванням:
Тоді отримаємо рівняння множинної лінійної регресії:
Оцінки параметрів отриманої моделі знаходять методом найменших квадратів.
3. Обернені моделі Найпростіша обернена модель має вигляд:
Побудуємо графіки залежності в залежності від знаків параметрів В залежності від знаків Якщо Якщо
4. Степеневі моделі Степенева регресійна модель має вигляд:
Вона зводиться до лінійної за допомогою заміни:
В результаті отримують регресійну нелінійну модель:
Степенева регресійна модель
5. Показникові моделі Показникові моделі мають вигляд:
Отримують лінійну модель: Зауваження: регресійні моделі можуть мати також вигляд, в який окремими частинами входять нелінійні регресійні моделі різних типів, наприклад, до такого типу моделей належать виробнича крива Кобба-Дугласа з врахуванням науково-технічного прогресу, яка має вигляд:
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.68 (0.009 с.) |


 отримати вибіркову регресійну модель
отримати вибіркову регресійну модель 
 , то тоді за знайденими оцінками параметрів моделі
, то тоді за знайденими оцінками параметрів моделі 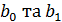 можна знайти інтервали, які з деякою імовірністю попадають в невідомі параметри
можна знайти інтервали, які з деякою імовірністю попадають в невідомі параметри  . Ці інтервали називаються довірчими інтервалами або інтервалами довіри.
. Ці інтервали називаються довірчими інтервалами або інтервалами довіри. (
(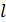 – рівень значимості, Р – рівень надійності) попадає в параметр
– рівень значимості, Р – рівень надійності) попадає в параметр 



 є неширокою, це означає, що оцінки параметрів
є неширокою, це означає, що оцінки параметрів  , якщо задане прогнозоване значення
, якщо задане прогнозоване значення  . Прогнозоване значення
. Прогнозоване значення 





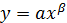
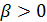 (1)
(1)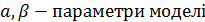
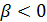 . Ці криві при такому розумінні називаються кривими Енгеля.
. Ці криві при такому розумінні називаються кривими Енгеля.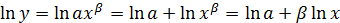
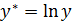 ,
, 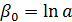 ,
, 
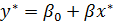 . Параметри отриманої моделі можна знайти методом найменших квадратів. Якщо знайдені оцінки параметрів
. Параметри отриманої моделі можна знайти методом найменших квадратів. Якщо знайдені оцінки параметрів  та
та  , тобто отримано вибіркову модель
, тобто отримано вибіркову модель 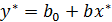 , тоді оцінки параметрів моделі (1) знаходять за формулою:
, тоді оцінки параметрів моделі (1) знаходять за формулою: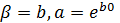
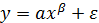 . При зведенні її до лінійної моделі ми опускали випадкову складову
. При зведенні її до лінійної моделі ми опускали випадкову складову  . Для того, щоб знайти оцінки параметрів отриманої лінійної моделі методом найменших квадратів випадкова складова цієї лінійної моделі повинна задовольняти ряд припущень. Тому виникає задача знаходження тих умов і припущень, які потрібно накладати на випадкову складову нелінійної моделі.
. Для того, щоб знайти оцінки параметрів отриманої лінійної моделі методом найменших квадратів випадкова складова цієї лінійної моделі повинна задовольняти ряд припущень. Тому виникає задача знаходження тих умов і припущень, які потрібно накладати на випадкову складову нелінійної моделі.
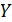 – обсяг (об’єм) продукції
– обсяг (об’єм) продукції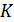 – основний капітал
– основний капітал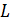 – робоча сила
– робоча сила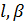 – параметри моделі.
– параметри моделі.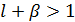 , то темпи приросту обсягу продукції вищі за темпи росту виробничих ресурсів.
, то темпи приросту обсягу продукції вищі за темпи росту виробничих ресурсів. , то навпаки, тобто темпи росту продукції нижчі за темпи росту ресурсів.
, то навпаки, тобто темпи росту продукції нижчі за темпи росту ресурсів.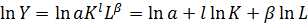


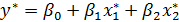
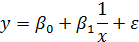
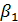 (графіки).
(графіки). , модель відображає залежність між доходом х і витратами на предмети розкоші у. Величина
, модель відображає залежність між доходом х і витратами на предмети розкоші у. Величина  – мінімально необхідний рівень доходів для придбання предметів розкоші. В цьому випадку отриманий графік залежності називається кривою (функцією) Торнквіста.
– мінімально необхідний рівень доходів для придбання предметів розкоші. В цьому випадку отриманий графік залежності називається кривою (функцією) Торнквіста.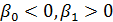 , то обернена залежність відображає залежність між рівнем безробіття х і процентною зміною заробітної плати у. Відповідна крива називається кривою Філіпса. Точка перетину з віссю ОХ – це природній рівень безробіття.
, то обернена залежність відображає залежність між рівнем безробіття х і процентною зміною заробітної плати у. Відповідна крива називається кривою Філіпса. Точка перетину з віссю ОХ – це природній рівень безробіття.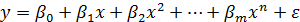
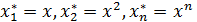
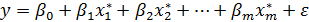
 – вони зводяться до лінійних за допомогою логарифмування:
– вони зводяться до лінійних за допомогою логарифмування: