
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи усунення мультиколінеарностіСодержание книги
Поиск на нашем сайте
В залежності від того, для чого будується економетрична модель при наявності мультиколінеарності поступають одним із двох способів: Якщо модель будується для прогнозування, то при великому значенні коефіцієнта детермінації (≈1) і при умові зберігання залежності між змінними мультиколінеарність не усувають з моделі. Також мета дослідження за допомогою економетричної моделі – це визначення міри впливу кожної незалежної змінної (фактору) на залежну змінну, тоді наявність колінеарності приводить до збільшення стандартних помилок, то це може приводити до неправильних висновків про вплив незалежних змінних на залежну, тоді мультиколінеарність з моделі потрібно усунути за допомогою одного із методів. Основними методами усунення мультиколінеарності є: 1. Використання первинної інформації. Суть: використовуючи економічну теорію встановлюють вигляд залежності між деякими коефіцієнтами моделі, які відповідають тим змінним моделям, які є залежні між собою. Наприклад: нехай досліджується залежність споживання від доходу та багатства. І економетрична модель має вигляд: y=β_0+β_1 x_1+β_2 x_2+ε, де y – споживання β_0 – дохід β_2 – багатство Якщо її розглядати для певної групи сімей, для якої відомо з економічного аналізу β_2=0,3β_1, тоді цю модель можна записати у вигляді: y=β_0+β_1 x_1+0,3β_1 x_2+ε=β_0+β_1 (x_1+0,3x_2)+ε x^* β_0+β_1 x^*+ε В отриманій моделі одна незалежна змінна x^*, знайшовши оцінку параметра b_1, отримаємо оцінку параметра b_2=0,3b_1. 2. Із економетричної моделі вилучають (викидають) незалежну змінну з великим значенням кореляції. Так в попередньому прикладі можна упустити x_2, яка відповідає фактору багатства. 3. Змінюють специфікацію (вигляд) моделі – в модель включають додаткову пояснювальні змінні, які мають вплив на залежну змінну, а також можливо змінюють саму форму (формулу) залежності від незалежних змінних. 4. Збільшують кількість спостережень. При збільшенні кількості спостережень, особливо при збільшенні об’єму вибірки можливо в деяких цих спостереженнях мультиколінеарність може бути відсутньою, при чому збільшення об’єму вибірки зменшує оцінки похибок коефіцієнтів і тим самим збільшує їх статистичну значимість. 5. Перетворення змінних в моделі. Використовуючи зв'язок між економічними показниками (змінними), які є корельовано між собою намагаються здійснити їх перетворення так, щоб в новій отриманій моделі усунути цю кореляцію. Наприклад: нехай в моделі y=β_0+β_1 x_1+β_2 x_2+ε змінні x_1 та x_2 є корельовано між собою, тоді замість цієї моделі можна розглянути модель: y/x_1 =β_0^*+β_2^* x_2/x_1 +u Отримана модель, в якій присутні відносні величини y/x_1 та x_2/x_1. Алгоритм Фарара-Глобера Для встановлення наявності мультиколінеарності розроблені різні типи та алгоритми. Одним з них є алгоритм Фарара-Глобера – ций алгоритм дає змогу встановлювати наявність мультиколінеарності між всіма незалежними змінними, кожної незалежної змінної з рештою змінних і кожної пари незалежних змінних. Цей алгоритм використовує три типи параметрів:
Нехай перевірка наявності мультиколінеарності між всіма змінними здійснюється ступним чином: 1. Нормалізують (стандартизують) змінні згідно формули:
2. Знаходять кореляційну матрицю нормалізованих змінних за формулою:
3. Обчислюється визначник матриці R. 4. Вибирають критерій
Вважають, що цей критерій має розподіл з 5. Формулюють статистичні гіпотези: Н0 – мультиколінеарність між змінними відсутня; Н1– мультиколінеарність між змінними присутня; За формулою знаходять фактичне значення критерію 6. За таблицями знаходять теоретичне значення Якщо Якщо Перевірка наявності мультиколінеарності деякої змінної з іншими змінними здійснюється за допомогою F-критерію наступним чином: 1. Знаходять обернену матрицю до мтариці 2. Вибирають для кожної змінної
3. Формулюють гіпотези Н0 – змінна Н1– змінна 4. Знаходять фактичне значення критерію 5. За таблицею розподілу Фішера знаходять теоретичне знчення критерію 6. Якщо Якщо Для перевірки наявності колінеарності між кожною парою незалежних змінних використовують t-критерій наступним чином: 1. Для довільних змінних
Частинні коефіцієнти кореляції 2. Вибирають критерій 3. Формулюють статистичні гіпотези: Нульова гіпотеза: Альтернативна гіпотеза: 4. Знаходять фактичне значення критерію 5. За таблицями t-розподілу знаходять теоретичне значення критерію 6. Якщо Якщо
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.104 (0.009 с.) |

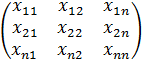
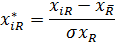
 , де
, де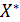 – матриця нормалізованих значень вибірки.
– матриця нормалізованих значень вибірки.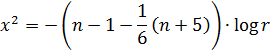
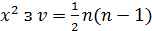 ступенями вільності.
ступенями вільності. .
.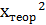 при
при 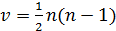 ступенях вільності і задану у вигляді значимості
ступенях вільності і задану у вигляді значимості 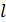 .
.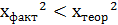 , то приймається нульова гіпотеза і вважається, що мультиколінеарність між змінними відсутня.
, то приймається нульова гіпотеза і вважається, що мультиколінеарність між змінними відсутня.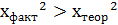 , то приймається альтернативна гіпотеза і вважається, що мультиколінеарність між змінними присутня.
, то приймається альтернативна гіпотеза і вважається, що мультиколінеарність між змінними присутня.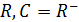
 F-критерій вигляд:
F-критерій вигляд: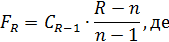
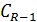 – це діагональні елементи матриці С вважають, що цей критерій Фішера з
– це діагональні елементи матриці С вважають, що цей критерій Фішера з 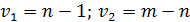 ступенями вільності.
ступенями вільності.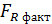
 , для
, для 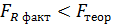 , то вважають, що змінна
, то вважають, що змінна  , то приймається альтернативна гіпотеза та вважають, що змінна
, то приймається альтернативна гіпотеза та вважають, що змінна 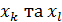 знаходять частинні коефіцієнти кореляції за формулою:
знаходять частинні коефіцієнти кореляції за формулою: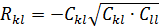
 - характеризують тісноту зв’язку між змінними
- характеризують тісноту зв’язку між змінними  , вважають, що він має t-розподіл з
, вважають, що він має t-розподіл з 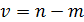 ступенями вільності.
ступенями вільності.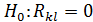
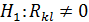

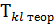 , для
, для 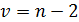 і вибираємо
і вибираємо 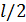 .
.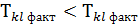 , то змінні
, то змінні 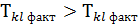 , то приймається альтернативна гіпотеза і змінні
, то приймається альтернативна гіпотеза і змінні 


