Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття гетероскедастичності та її наслідкиСодержание книги
Поиск на нашем сайте
Розглянемо економетрична модель множинної лінійної регресії:
Оцінку параметрів моделі можна знаходити методом найменших квадратів, якщо випадкова складова мала нормальний закон розподілу і сталу дисперсію. Зокрема, сталість дисперсії означала, що Якщо дисперсія залишків стала (постійна) для кожного спостереження, то ця властивість дисперсії називається гомоскедастичністю. Гомоскедастичність означає, що ймовірність того, що випадкова величина Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень це явище називається гетероскедастичність. (графіки) Наслідки: висновки відносно оцінок параметрів моделі, інтервалі довіри, а також відносно перевірки статистичних гіпотез можуть бути хибними (невірними). Це пов’язано з тим, що оцінка дисперсії помилок при наявності гетероскедастичності не може бути обчислена за формулою:
Для перевірки встановлення наявності гетероскедастичності є різні методи, які залежать від об’єму вибірки. До основних з них можна віднести: s s s Тест Глейсера; s Тест Голтфельда-Квандта. Ідея всіх тестів полягає в тому, що в апріорі вважають, що дисперсія залишків має певну залежність. Вид цієї залежності встановлюється з різних припущень.
Тест Голдфельда-Квандта Розглянемо тест Голдфельда-Квандта. Припустимо, що дисперсія залишків моделі змінюється пропорційно до квадрату однієї змінної
Ідея тесту: вся вибірка впорядковується в порядку зростання змінної Алгоритм тесту: 1. Вибірку впорядковують по зростанню фактора
2. Розбивають вибірку на три частини. Значення c вибирають таким чином, щоб 3. З вибірки викидають середні значення. 4. Для першої і третьої частин вибірки знаходять методом найменших квадратів оцінки параметрів моделі. В результаті отримують дві вибіркові регресійні прямі:
5. Знаходять суми квадратів залишків для кожної із моделей:
6. Задають F-критерій:
Вважають, що він має розподіл Фішера з 7. Формулюють статистичні гіпотези:
8. Знаходять фактичне значення критерію 9. За таблицями розподілу Фішера знаходять критичне значення 10. Якщо
13. Знаходження оцінок параметрів моделі за допомогою узагальненого методу найменших квадратів (метод Ейткена) При наявності гетероскедастичності оцінки параметрів моделі, які отримані методом найменших квадратів є неефективними, тобто вони не будуть мати найменшу дисперсію, порівняно з оцінками параметрів моделі отриманих іншими методами. Для знаходження ефективних оцінок параметрів потрібно використати інші методи. Одним з таких методів є узагальнений метод найменших квадратів (метод Ейткена). Суть методу: вихідну економетрична модель в якій присутня гетероскедастичність за допомогою певного перетворення приводять до моделі, в якій присутня гомоскедастичність. Перетворення вихідної моделі в гомоскедастичну відбувається шляхом коригування (перетворення) вихідної інформації стосовно змінних моделі. Для цього використовується вигляд залежності дисперсії залишків від тієї чи іншої змінної моделі. Враховуючи вигляд цієї залежності за певними правилами будують (формують) квадратну матрицю S, розмір якої співпадає з об’ємом (розмірністю) вибірки. Формула для оцінки параметрів моделі тоді матиме вигляд:
Якщо, наприклад, вважати, що дисперсія залишків пропорційна до зміни незалежної змінної
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.39 (0.005 с.) |


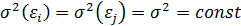 , для довільних спостережень і, j.
, для довільних спостережень і, j. набуває визначене значення буде однаковою для всіх спостережень.
набуває визначене значення буде однаковою для всіх спостережень.
 -тест – для великого об’єму вибірки;
-тест – для великого об’єму вибірки; ест Парка;
ест Парка; моделі, тобто:
моделі, тобто: , де
, де 
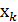 (всі елементи вибірки):
(всі елементи вибірки):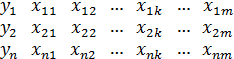
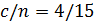 .
.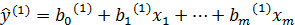
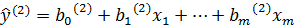
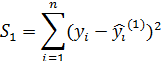
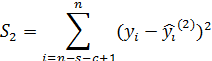
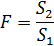
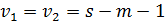 ступенями вільності.
ступенями вільності.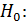 присутня гомоскедастичність
присутня гомоскедастичність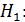 присутня гетероскедастичність
присутня гетероскедастичність .
.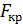 для
для 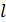 .
.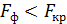 , приймається нульова гіпотеза і вважається, що присутня гомоскедастичність. Якщо
, приймається нульова гіпотеза і вважається, що присутня гомоскедастичність. Якщо  , приймається альтернативна гіпотеза і вважається, що присутня гетероскедастичність.
, приймається альтернативна гіпотеза і вважається, що присутня гетероскедастичність.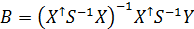
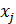 , тоді матриця S матиме вигляд:
, тоді матриця S матиме вигляд: