
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистична перевірка гіпотез про закон розподілуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистичною гіпотезою називається гіпотеза про вигляд невідомого розподілу генеральної сукупності або про параметри відомих розподілів. Процес використання вибірки для перевірки істинності (хибності) статистичної гіпотези називають статистичною перевіркою цієї гіпотези. Одна з основних задач статистичної перевірки гіпотез ставиться так: на підставі тих чи інших даних висувається припущення про вид закону розподілу випадкової величини Х. Потрібно встановити, чи узгоджуються вибіркові значення Х з гіпотезою про те, що ця випадкова величина дійсно має вказаний розподіл. Для перевірки гіпотези про те, що випадкова величина Х має функцію розподілу F (x), за вибіркою значень Х будують емпіричну функцію розподілу F* (x). Порівняння емпіричного F* (x) і теоретичного F (x) розподілів здійснюється за допомогою спеціально підібраної випадкової величини – критерію згоди. Найбільш поширеними є критерій згоди c2 Пірсона і критерій l Колмогорова. Критерій згоди c2 Нехай маємо результати n незалежних дослідів (вибірка об’єму n). Весь діапазон результатів розбиваємо на l інтервалів D1, D2, …, D l і будуємо інтервальний варіаційний ряд
де Для перевірки гіпотези про те, що випадкова величина Х має функцію розподілу F (x), виконують таку послідовність дій. 1. За допомогою гіпотетичної функції розподілу F (x) обчислюють імовірності pi попадання випадкової величини Х в інтервали D i. Якщо, наприклад, D i = [ xi – 1, xi [, то pi = P (xi – 1 £ X < xi) = F (xi) – F (xi – 1) 2. Перемножаючи отримані ймовірності pi на об’єм вибірки n, знаходять теоретичні частоти npi для інтервалів D i. 3. Обчислюють вибіркову статистику (критерій) c2:
4. Визначають число k ступенів свободи за формулою k = l – r – 1, де l – число інтервалів, r – число параметрів, які характеризують гіпотетичний розподіл F (x). 5. За заданим рівнем значущості a і числом ступенів свободи k знаходять з таблиці додатку 5 критичну точку
Критерій згоди l Колмогорова
Нехай висунута гіпотеза, що випадкова величина Х має неперервну функцію розподілу F (x). За вибіркою значень Х об’єму n (n ³ 50) перевірку висунутої гіпотези за допомогою критерію згоди l Колмогорова виконують у такій послідовності. 1. За результатами вибірки будують емпіричну функцію розподілу F* (x). 2. За допомогою гіпотетичної функції розподілу обчислюють значення теоретичної функції розподілу, що відповідають вибірковим значенням випадкової величини Х. 3. Знаходять міру D відхилення теоретичної функції розподілу від емпіричної
4. Обчислюють значення вибіркової статистики l
5. За заданим рівнем значущості a з таблиці додатку 4 знаходять критичну точку la. Якщо l спост > la, то висунута гіпотеза відхиляється. Якщо ж l спост < la, то вважається, що гіпотетична функція розподілу F (x) узгоджується з дослідними даними.
Опитування з теорії 1. Що називається статистичною гіпотезою про закон розподілу? Як перевіряються гіпотези про закон розподілу? 2. Як перевіряється гіпотеза про закон розподілу за допомогою критерію згоди c2 (критерію Пірсона)? 3. Як перевіряється гіпотеза про закон розподілу за допомогою критерію згоди l Колмогорова? 4. Які умови мають виконуватися при застосуванні критеріїв Пірсона і Колмогорова?
Задача 1. З генеральної сукупності Х здійснена вибірка об¢єму n =100, яка задана у вигляді послідовності інтервалів і відповідних їм частот
Перевірити за допомогою критерію c2 при рівні значущості 0,05 гіпотезу про нормальний розподіл генеральної сукупності. Розв¢язання. З умови задачі випливає, що точні значення параметрів а = M (X) і s = s(X) гіпотетичного нормального розподілу нам невідомі, тому замість них будемо використовувати їх точкові оцінки
=13,8;
Обчислюємо теоретичні ймовірності pi попадання випадкової величини Х в часткові інтервали [ xi – 1, xi [за формулою
де
Всі подальші обчислення, необхідні для знаходження значення
Контроль: З останнього стовпця таблиці отримуємо
За таблицею критичних точок розподілу c2 (додаток 5) при рівні значущості a = 0,05 і числі ступенів свободи k = l – r – 1 = 7 – 2 – 1 = 4 знаходимо критичну точку Оскільки Задача 2. Задані результати випробування 1000 елементів на час безвідмовної роботи. Перевірити за допомогою критерію c2 при рівні значущості 0,01 гіпотезу про те, що час Х безвідмовної роботи елементів розподілений за показниковим законом.
Розв¢язання. Параметр l гіпотетичного показникового розподілу невідомий, тому замість нього будемо використовувати його точкову оцінку
Отже,
Обчислюємо теоретичні ймовірності pi попадання випадкової величини Х в часткові інтервали [ xi – 1, xi [за формулою
Всі подальші обчислення, необхідні для знаходження значення
Контроль: Зауваження. Оскільки випадкова величина Х, розподілена за показниковим законом, приймає значення в інтервалі ] 0; + ¥[, то найбільше значення змінної замінено на + ¥. З останнього стовпця таблиці отримуємо
За таблицею критичних точок розподілу c2 (додаток 5) при рівні значущості a = 0,01 і числі ступенів свободи k = l – r – 1 = 7 – 1 – 1 = 5 знаходимо критичну точку Оскільки Задача 3. З генеральної сукупності Х здійснена вибірка об¢єму n =100, яка задана у вигляді послідовності інтервалів і відповідних їм частот
Вважаючи відомими a = M (X)=10, s=s(X)=4, перевірити за допомогою критерію l Колмогорова при рівні значущості 0,05 гіпотезу про те, що вибірка здійснена з нормально розподіленої генеральної сукупності. Розв’язання. Функція розподілу випадкової величини Х, розподіленої за нормальним законом з параметрами a = 10, s = 4, має вигляд
За вибірковими даними (n = 100) обчислюємо значення емпіричної функції розподілу
З останнього стовпця таблиці знаходимо
Обчислюємо значення вибіркової статистики l
і за таблицею критичних точок розподілу Колмогорова (Додаток 4) при рівні значущості a = 0,05 знаходимо критичну точку la = 1,358. Оскільки l спост < la, то нема підстав для відхилення гіпотези про нормальний розподіл генеральної сукупності. Задача 4. Результати вимірювання однотипних деталей наведені в таблиці
Перевірити за допомогою критерію l Колмогорова при рівні значущості 0,01 гіпотезу про те, що вибірка здійснена з генеральної сукупності, рівномірно розподіленої в проміжку [40,10; 40,60]. Розв’язання. Функція розподілу випадкової величини, рівномірно розподіленої в проміжку [40,10; 40,60], має вигляд
За вибірковими даними (n = 80) обчислюємо значення емпіричної функції розподілу
З останнього стовпця таблиці знаходимо
Обчислюємо значення вибіркової статистики l
і за таблицею критичних точок розподілу Колмогорова (Додаток 4) при рівні значущості a = 0,01 знаходимо критичну точку la = 1,627. Оскільки l спост < la, підстав для відхилення гіпотези про рівномірний розподіл генеральної сукупності нема.
Задачі для аудиторної та самостійної роботи
1. Результати вимірювання 68 деталей, виготовлених на одному станку, наведені в таблиці
Перевірити за допомогою критерію c2 при рівні значущості 0,01 гіпотезу про нормальний розподіл випадкової величини Х – розмір деталі. Відповідь: Гіпотеза приймається. 2. Результати вимірювання вхідного опору 130 електронних ламп наведені в таблиці
Перевірити за допомогою критерію c2 при рівні значущості 0,01 гіпотезу про нормальний розподіл випадкової величини Х – вхідний опір електронної лампи. Відповідь: Гіпотеза відхиляється. 3. Задані результати випробування елементів на час безвідмовної роботи. Перевірити за допомогою критерію c2 при рівні значущості 0,01 гіпотезу про те, що час безвідмовної роботи елементів розподілений за показниковим законом.
Відповідь: a) Гіпотеза приймається; б) гіпотеза приймається. 4. За допомогою радіодальноміра проведено 100 вимірювань відстані до орієнтира. Похибки хі вимірювань відстані (в метрах) наведені в таблиці
Перевірити за допомогою критерію l Колмогорова при рівні значущості 0,01 гіпотезу про те, що вибірка здійснена з нормально розподіленої генеральної сукупності. Відповідь: Гіпотеза приймається. 5. Результати вимірювання однотипних деталей наведені в таблиці
Перевірити за допомогою критерію l Колмогорова при рівні значущості 0,01 гіпотезу про те, що вибірка здійснена з генеральної сукупності, рівномірно розподіленої в проміжку [20,2; 20,7]. Відповідь: Гіпотеза приймається.
Практичне заняття 12
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.38.5 (0.008 с.) |

 .
. .
.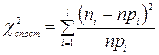 . (11.1)
. (11.1) . Якщо
. Якщо  , висунуту гіпотезу відхиляють, тобто вважається, що гіпотетична функція розподілу F (x)не узгоджується з дослідними даними. Якщо ж
, висунуту гіпотезу відхиляють, тобто вважається, що гіпотетична функція розподілу F (x)не узгоджується з дослідними даними. Якщо ж  , то вважається, що гіпотетична функція розподілу F (x) узгоджується з дослідними даними.
, то вважається, що гіпотетична функція розподілу F (x) узгоджується з дослідними даними.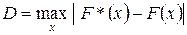 .
. . (11.2)
. (11.2) і s. Для обчислення цих оцінок визначаємо середини xi* інтервалів і проводимо розрахунки:
і s. Для обчислення цих оцінок визначаємо середини xi* інтервалів і проводимо розрахунки:

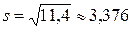 .
.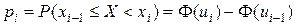 ,
, – функція Лапласа.
– функція Лапласа. , зводимо в наступну таблицю
, зводимо в наступну таблицю
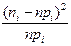
 .
. .
.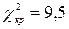 .
. , то нема підстав для відхилення гіпотези про нормальний розподіл генеральної сукупності.
, то нема підстав для відхилення гіпотези про нормальний розподіл генеральної сукупності. . Вибіркову середню
. Вибіркову середню  (середній час безвідмовної роботи одного елемента) обчислюємо за допомогою середин інтервалів
(середній час безвідмовної роботи одного елемента) обчислюємо за допомогою середин інтервалів 
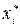 :
: (5×365+15×245+25×150+35×100+45×70+55×45+65×25) = 20.
(5×365+15×245+25×150+35×100+45×70+55×45+65×25) = 20. і щільність гіпотетичного показникового розподілу має вигляд
і щільність гіпотетичного показникового розподілу має вигляд (x > 0).
(x > 0).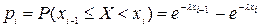 .
. .
. .
. .
. , тому гіпотезу про показниковий розподіл генеральної сукупності слід відхилити.
, тому гіпотезу про показниковий розподіл генеральної сукупності слід відхилити. , де
, де  - функція Лапласа.
- функція Лапласа. , теоретичної функції розподілу F (x) і абсолютні величини різниць F *(xi) – F (xi). Результати обчислень зводимо в таблицю
, теоретичної функції розподілу F (x) і абсолютні величини різниць F *(xi) – F (xi). Результати обчислень зводимо в таблицю .
.

 .
.



