
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування комбінаторики для підрахунку ймовірності подій. Теореми додавання та множення ймовірностей
Елементи комбінаторики. Розміщення, перестановки, комбінації Комбінаторика – це розділ математики, що вивчає скінченні множини, тобто такі, що містять скінченну кількість елементів. Основний принцип комбінаторики (правило множення ): якщо деякий вибір (дію) можна виконати Нехай є множина М, що має Розміщенням з Розміщення з Комбінацією (сполукою) з
Теорема додавання ймовірностей для несумісних подій Якщо А і В несумісні події, тобто Наслідки. 1) Якщо події
2) Ймовірність протилежної до А події 3) Сума ймовірностей подій
Теорема додавання ймовірностей для сумісних подій Ймовірність суми двох подій дорівнює сумі ймовірностей цих подій без імовірності їх добутку: Наслідок. Ймовірність суми трьох подій знаходиться за формулою:
Умовною ймовірністю події А за умови, що відбулась подія В, називається величина
Теорема множення ймовірностей для двох подій
Випадкові події А і В називаються незалежними, якщо
Для незалежних подій настання однієї з подій не впливає на ймовірність другої події:
Теорема множення ймовірностей для Якщо
Випадкові події Ймовірність настання хоча б однієї події з подій
Опитування з теорії
1.Сформулювати основний принцип комбінаторики. 2.Що таке розміщення, перестановки, комбінації, як визначається їх число? 3.Сформулювати теорему додавання для несумісних подій; для сумісних подій. 4.Дати означення умовної ймовірності та сформулювати теорему множення. 5.Які дві події називаються незалежними? 6.Дати означення незалежних в сукупності подій; попарно незалежних. 7.Як визначається ймовірність настання хоча б однієї події з незалежних в сукупності подій? Задача 1. Набираючи номер телефону, абонент забув дві останні цифри і набрав їх навмання, пам’ятаючи, що вони різні і непарні. Яка ймовірність, що номер телефону набрано правильно? Розв’язання. Опишемо простір елементарних подій експерименту. Результатом експерименту є пара упорядкованих чисел Задача 2. На картках написані цифри 1,2,…,9. Навмання беруть 4 картки і викладають їх в ряд. Яка ймовірність, що отримають парне число? Розв’язання. Опишемо простір елементарних подій експерименту. Елементарною подією є впорядкована четвірка не співпадаючих чисел з множини (1,2,…,9). Це розміщення з 9 елементів по 4, їх число Задача 3. Яка ймовірність вгадати код, установлений на камері схову, якщо це 5 - значне число, що складається з нулів і одиниць? Розв’язання. Простір елементарних подій в цьому експерименті – сукупність різних 5-значних чисел, складених з нулів і одиниць. Знайдемо їх число. Для вибору кожної цифри 5-значного числа є 2 варіанти – 0 або 1, тому за правилом множення варіанти множаться і їх буде
Задача 4. Яка ймовірність зайти в під’їзд, якщо для цього потрібно набрати тризначне число (код), знаючи, що воно: 1) непарне і ділиться на 3; 2) непарне і не містить однакових цифр. Розв’язання. 1)Опишемо простір елементарних подій.Він складається з різних тризначних непарних чисел, що діляться на 3. Знайдемо їх число. Від 100 до 1000 буде 300 чисел що діляться на3, оскільки Задача 5. Знайти ймовірність того, що навмання взяте тризначне число буде парне число, що ділиться на 3. Розв’язання Простір елементарних подій буде множина довільних тризначних чисел. Їх число буде Задача 6. Яка ймовірність з 36 номерів (елементів), надрукованих на картці, вгадати 6, 5, 4, 3, викреслюючи 6 з 36 (лотерея спортлото)? Яка ймовірність отримати виграш (вгадавши від 3 до 6 номерів)? Розв’язання. Простір елементарних подій експерименту складається з неупорядкованих множин по 6 елементів. Таких подій буде стільки, скільки є комбінацій з 36 по 6: Задача 7. З урни, що містить 5 чорних і 7 білих куль, послідовно вийняли дві кулі. Обчислити ймовірність того, що: 1) обидві вийняті кулі чорні; 2) обидві вийняті кулі білі; 3) одна куля чорна і одна біла. Розв’язання. Будемо вважати кулі занумерованими. Нехай 5 чорних куль мають номери 1, 2,…, 5, а 7 білих мають номери 6, 7,…, 12. Елементарна подія це упорядкована пара чисел, наприклад (3,6) означає, що першою вийняли чорну кулю з номером 3, а другою – білу кулю з номером 6. Число елементарних подій
3) Знайдемо ймовірність, що одна куля чорна і одна біла. Вважаючи, що першою вийняли чорну кулю (а другою білу), будемо мати число сприятливих подій Зауваження. Оскільки у запитаннях, які стоять до задачі, порядок, у якому виймають кулі, не важливий, то можна вважати, що кулі виймають одночасно. Тоді число елементарних подій – це число комбінацій з 12 по 2: Задача 8. Розв’язання. 1)Елементарна подія – довільна перестановка з Задача 10. В урні знаходяться кулі трьох кольорів: 4 чорних, 5 білих і 6 синіх. 1) Яка ймовірність вийняти по черзі чорну, білу і синю кулю (у вказаному порядку)? 2) Яка ймовірність вийняти ці кулі у будь-якому порядку (подія Е)? Розв’язання. 1) Позначимо: А – першою вийняли чорну кулю, В – другою вийняли білу кулю, С – третьою вийняли синю кулю. Позначимо через
Задача 11. Три електроприлади працюють або виходять з ладу незалежно один від одного. Ймовірність вийти з ладу за час Т для першого приладу дорівнює 0,1; для другого 0,2; для третього 0,3. Знайти ймовірності таких подій: 1) не вийде з ладу жодний прилад; 2) вийде з ладу тільки один прилад; 3) будуть працювати не менше двох приладів; 4) всі прилади будуть працювати; 5) вийде з ладу не більше одного приладу. Розв’язання. 1) Позначимо через 4) Задача 12. Скільки разів потрібно підкинути монету, щоб з імовірністю не менше 0,99 хоч один раз випав герб? Розв’язання. Позначимо
Задачі для аудиторної та самостійної роботи
1. Підкидається гральний кубик по черзі два рази. Знайти ймовірність, що: 1)один раз випаде 6; 2) два рази випаде 6; 3) хоч один раз випаде 6. Відповідь: 1) 1/6; 2) 1/36; 3)11/36. 2. На шахову дошку розмірами 3. Серед 100 деталей є 5 бракованих. Навмання взяли 10 деталей. Яка ймовірність, що серед них є 3 браковані? Відповідь:
4. В ліфт 8-поверхового будинку на першому поверсі зайшли 5 осіб. Припускаємо, що кожна особа може вийти на будь-якому з 7 поверхів з однаковою ймовірністю. Знайти ймовірність, що всі 5 осіб вийдуть на різних поверхах. Відповідь: 5. Яка ймовірність, що числа 1, 2, 3 будуть стояти поруч і в порядку зростання при довільній перестановці чисел 1, 2, …, Відповідь: 6. З колоди в 52 карти навмання беруть 3 карти. Яка ймовірність, що це трійка, сімка, туз? Відповідь: 8. Навмання вибрано кістку доміно. Знайти ймовірність, що другу навмання взяту кістку можна приставити до першої, якщо перша виявилась: а)дублем; б) не дублем. Відповідь: а) 1/18; б)1/3. 9. Дві команди кожна з 10 спортсменів проводять жеребкування для присвоєння номерів учасникам змагань. Два брати входять до складу різних команд. Знайти ймовірність, що обидва брати будуть мати: а) номер 5; б) один і той самий номер. Відповідь: а) 0,01; б) 0,1. 10. З ящика, в якому перемішані 10 чорних, 12 синіх і 8 білих куль, студент навмання дістає дві кулі. Яка ймовірність, що він дістав: а) 2 синіх кулі; б) 2 кулі одного кольору? Відповідь: а) 0,347;б) 0,732. 11. Серед студентів університету було проведено дослідження на частоту захворювань на протязі останнього року на такі хвороби: застуда (І), грип (ІІ), ангіна (ІІІ), алергія (IV). Виявлені такі дані: на І хворобу хворіло 0,9 від усього числа студентів; на ІІ –0,6; на ІІІ –0,3; на IV – 0,4. Яка ймовірність, що навмання взятий студент: а) зовсім не хворів; б)хворів на І і ІІ або на ІІІ і IV хвороби; в) хворів тільки на одну хворобу; г) хворів на всі чотири хвороби? Відповідь:а) 0,0168; б) 0,2316; в) 0,2; г) 0,0648. 12. Скільки разів потрібно підкинути гральний кубик, щоб з імовірністю не меншою 0,9 хоч один раз випало 6 очок? Відповідь: 13.
Практичне заняття 3
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.141.202 (0.046 с.) |
 способами, після чого другий вибір можна виконати
способами, після чого другий вибір можна виконати 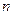 способами, то разом обидва вибори можна виконати
способами, то разом обидва вибори можна виконати 
 способами. Це правилосправедливе для будь-якого скінченного числа виборів (дій).
способами. Це правилосправедливе для будь-якого скінченного числа виборів (дій). називається довільна впорядкована множина з
називається довільна впорядкована множина з 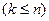 знаходиться за формулою
знаходиться за формулою  .
. елементів по
елементів по  .
. .
. , то
, то  .
. попарно несумісні, тобто
попарно несумісні, тобто  , то
, то .
. дорівнює
дорівнює 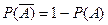 .
. =1.
=1. .
. .
. .
. або
або  .
. .
. .
. – довільні події, то
– довільні події, то  .
. для будь-яких
для будь-яких 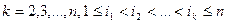 . Ці події називаються попарно незалежними, якщо рівність виконується для
. Ці події називаються попарно незалежними, якщо рівність виконується для  , тобто для будь-яких двох подій.
, тобто для будь-яких двох подій. , де
, де 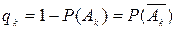 .
. де
де  приймають не співпадаючі значення з множини (1,3,5,7,9); число таких пар за основним принципом комбінаторики буде
приймають не співпадаючі значення з множини (1,3,5,7,9); число таких пар за основним принципом комбінаторики буде 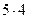 =20. Це розміщенняз 5 елементів по 2. Маємо 20 елементарних подій і тільки одна з них сприятлива (правильна пара цифр), тому шукана ймовірність
=20. Це розміщенняз 5 елементів по 2. Маємо 20 елементарних подій і тільки одна з них сприятлива (правильна пара цифр), тому шукана ймовірність  .
. . Знайдемо число сприятливих елементарних подій. Елементарна подія є сприятливою, якщо крайня права цифра парна, а саме, приймає значення з множини (2,4,6,8). Вважаючи, що спочатку ми вибираємо останню цифру, будемо мати для її вибору 4 варіанти
. Знайдемо число сприятливих елементарних подій. Елементарна подія є сприятливою, якщо крайня права цифра парна, а саме, приймає значення з множини (2,4,6,8). Вважаючи, що спочатку ми вибираємо останню цифру, будемо мати для її вибору 4 варіанти  , для вибору трьох інших карток маємо
, для вибору трьох інших карток маємо 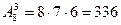 варіантів, тому число сприятливих виборів буде
варіантів, тому число сприятливих виборів буде  Отже, шукана ймовірність
Отже, шукана ймовірність  .
. . Сприятливий варіант тільки один – правильне число, тому шукана ймовірність
. Сприятливий варіант тільки один – правильне число, тому шукана ймовірність  .
. , перше з них – 102, останнє 999. Треба відкинути парні числа, тобто ті, що діляться і на 2, і на 3. Чисел, що діляться на 6 від 100 до 1000, буде 150, оскільки
, перше з них – 102, останнє 999. Треба відкинути парні числа, тобто ті, що діляться і на 2, і на 3. Чисел, що діляться на 6 від 100 до 1000, буде 150, оскільки  , перше з них 102, останнє 996, тоді непарних чисел, що діляться на 3, буде також 150. Тому шукана ймовірність
, перше з них 102, останнє 996, тоді непарних чисел, що діляться на 3, буде також 150. Тому шукана ймовірність 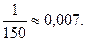
 елементарних подій. Припустимо тепер, що друга цифра 0,тоді буде
елементарних подій. Припустимо тепер, що друга цифра 0,тоді буде  (5 варіантів для першої справа і 8 для третьої цифр) таких елементарних подій. Всього буде
(5 варіантів для першої справа і 8 для третьої цифр) таких елементарних подій. Всього буде  елементарних подій. Тому шукана ймовірність
елементарних подій. Тому шукана ймовірність 
 , оскільки перша зліва цифра може бути 1,2,…9, а друга і третя 0,1,2,…,9. Сприятливих подій буде стільки, скільки чисел, що діляться на 6 від 100 до 1000. Їх буде 150. Тому шукана ймовірність
, оскільки перша зліва цифра може бути 1,2,…9, а друга і третя 0,1,2,…,9. Сприятливих подій буде стільки, скільки чисел, що діляться на 6 від 100 до 1000. Їх буде 150. Тому шукана ймовірність 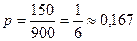 .
. . Тому ймовірність вгадати 6 номерів
. Тому ймовірність вгадати 6 номерів  . Розглянемо ймовірність вгадати 5 номерів. Число сприятливих подій буде
. Розглянемо ймовірність вгадати 5 номерів. Число сприятливих подій буде  , тобто 5 номерів повинні бути з «щасливого набору» (з 6 виграшних номерів) і один номер з «нещасливого». Тому
, тобто 5 номерів повинні бути з «щасливого набору» (з 6 виграшних номерів) і один номер з «нещасливого». Тому  . Розглянемо ймовірність вгадати 4 номери. Число сприятливих подій буде
. Розглянемо ймовірність вгадати 4 номери. Число сприятливих подій буде  , тобто 4 номери повинні бути з «щасливого набору» і 2 з «нещасливого». Тому
, тобто 4 номери повинні бути з «щасливого набору» і 2 з «нещасливого». Тому  . Тепер розглянемо ймовірність вгадати 3 номери. Число сприятливих подій буде
. Тепер розглянемо ймовірність вгадати 3 номери. Число сприятливих подій буде 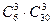 , тобто 3 номери повинні бути з «щасливого набору» і 3 з «нещасливого». Тому ймовірність
, тобто 3 номери повинні бути з «щасливого набору» і 3 з «нещасливого». Тому ймовірність  . Нарешті використовуючи теорему додавання ймовірностей для несумісних подій, знайдемо ймовірність отримати виграш:
. Нарешті використовуючи теорему додавання ймовірностей для несумісних подій, знайдемо ймовірність отримати виграш:  .
. . 1) Знайдемо ймовірність, що обидві вийняті кулі чорні. Сприятливих подій буде стільки, скільки розміщень з 5 елементів по 2:
. 1) Знайдемо ймовірність, що обидві вийняті кулі чорні. Сприятливих подій буде стільки, скільки розміщень з 5 елементів по 2:  , тому ймовірність
, тому ймовірність  .
.  .
.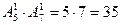 . Стільки ж подій будемо мати, коли першою вийняли білу кулю (а другою чорну). Всього70 сприятливих подій, тому ймовірність
. Стільки ж подій будемо мати, коли першою вийняли білу кулю (а другою чорну). Всього70 сприятливих подій, тому ймовірність  .
. , число сприятливих подій у першому випадку число комбінацій з 5 по 2
, число сприятливих подій у першому випадку число комбінацій з 5 по 2  , у другому випадку
, у другому випадку  ,у третьому випадку
,у третьому випадку  . Очевидно, що відповіді ті ж самі.
. Очевидно, що відповіді ті ж самі. . 2) Тут можна вважати, що при одночасному зміщенні всіх осіб на однакове число місць отримаємо те саме розміщення навколо стола, тому можна вважати, що особа А займає фіксоване місце. Всього елементарних подій буде стільки, скільки є перестановок з (
. 2) Тут можна вважати, що при одночасному зміщенні всіх осіб на однакове число місць отримаємо те саме розміщення навколо стола, тому можна вважати, що особа А займає фіксоване місце. Всього елементарних подій буде стільки, скільки є перестановок з (
 подію, що А, В, С виконуються одночасно. Знайдемо ймовірність події
подію, що А, В, С виконуються одночасно. Знайдемо ймовірність події  . Знайдемо ймовірність кожного множника:
. Знайдемо ймовірність кожного множника:  (всього куль 15, з них 4 чорних);
(всього куль 15, з них 4 чорних);  (залишилось 14 куль, з них 5 білих);
(залишилось 14 куль, з них 5 білих);  (залишилось 13 куль, з них 6 синіх). Тоді шукана ймовірність
(залишилось 13 куль, з них 6 синіх). Тоді шукана ймовірність  . 2) Розглянемо ймовірність вийняти ці три кулі у довільному порядку. Опишемо простір елементарних подій. Будемо вважати, що елементарна подія це набір з трьох довільних куль, таких подій буде
. 2) Розглянемо ймовірність вийняти ці три кулі у довільному порядку. Опишемо простір елементарних подій. Будемо вважати, що елементарна подія це набір з трьох довільних куль, таких подій буде  . Знайдемо число сприятливих подій, їх буде
. Знайдемо число сприятливих подій, їх буде  , оскільки одну кулю потрібно вибрати з чорних, одну з білих і одну з синіх. Тому шукана ймовірність
, оскільки одну кулю потрібно вибрати з чорних, одну з білих і одну з синіх. Тому шукана ймовірність  . Зауважимо, що ця ймовірність у 6 разів більша за
. Зауважимо, що ця ймовірність у 6 разів більша за  .
. подію – вийде з ладу перший прилад,
подію – вийде з ладу перший прилад,  – вийде з ладу другий прилад,
– вийде з ладу другий прилад,  – вийде з ладу третій прилад, А – не вийде з ладу жодний прилад. Протилежна до А подія – всі прилади вийдуть з ладу (подія
– вийде з ладу третій прилад, А – не вийде з ладу жодний прилад. Протилежна до А подія – всі прилади вийдуть з ладу (подія  ,
,  Р (
Р ( ; доданки, що входять в цю суму, є несумісні. За теоремою додавання ймовірностей для несумісних подій
; доданки, що входять в цю суму, є несумісні. За теоремою додавання ймовірностей для несумісних подій  і за теоремою множення
і за теоремою множення  . Таким чином,
. Таким чином,  .
.

 за теоремою додавання для несумісних подій. Оскільки подія
за теоремою додавання для несумісних подій. Оскільки подія  і
і 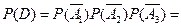
 за теоремою множенняймовірностей. Остаточно
за теоремою множенняймовірностей. Остаточно 
 5)
5) 
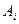 подію, що при і -му підкиданні випав герб; А – подію, що хоч один раз випав герб при п підкиданнях. Тоді
подію, що при і -му підкиданні випав герб; А – подію, що хоч один раз випав герб при п підкиданнях. Тоді  ; протилежна до А подія –ні разу не випаде герб має такий вигляд
; протилежна до А подія –ні разу не випаде герб має такий вигляд  . Знайдемо ймовірність останньої події
. Знайдемо ймовірність останньої події 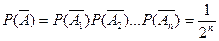 . Тому для
. Тому для  Знайдемо п з останньої нерівності
Знайдемо п з останньої нерівності  . Прологарифмуємо останню нерівність за основою 10. Будемо мати
. Прологарифмуємо останню нерівність за основою 10. Будемо мати 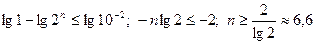 . Оскільки п ціле число, то
. Оскільки п ціле число, то  ставляться дві тури. Яка ймовірність, що вони не будуть бити одна одну? Відповідь: 49/33.
ставляться дві тури. Яка ймовірність, що вони не будуть бити одна одну? Відповідь: 49/33. .
.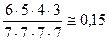 .
.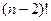 .
. .
.


